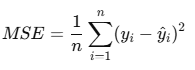- PyTorch
딥러닝에 사용되는 오픈소스 라이브러리(Numpy 등을 텐서로 가져올 수 있고 GPU 가속 기능(CUDA)을 지원한다.)
- CUDA: 그래픽 카드를 CPU처럼 사용할 수 있게 만들어줌. 보텅 하드웨어 가속 기능을 가리킨다.
- Learning Paradigm
Supervised Learning (지도 학습)
입력 데이터와 함께 목표/라벨이 제공되며, 모델은 이 라벨을 예측하도록 학습된다.
Unsupervised Learning (비지도 학습)
입력 데이터만 주어지며 모델은 데이터의 패턴을 찾도록 학습된다.
Reinforcement Learning (강화 학습)
주어진 환경과 상호작용하며 보상을 최대화하도록 학습한다.- Tensor: 일반화된 벡터이자 행렬이다. => 좌표변환 등의 연산을 고려하지 않는 단순히 데이터를 담은 다차원 배열이다. (Tesnor는 numpy 배열과 비슷하지만 GPU를 활용한 연산이 가능하다.)
- 데이터 준비
pandas, numpy를 활용해 데이터를 전처리하고, PyTorch의 Dataset과 DataLoader로 모델에 입력 가능한 형식으로 변환한다.
- Pandas란 무엇인가?
pandas는 Python의 데이터 분석,조작 라이브러리입니다.
엑셀이나 데이터베이스에서 데이터를 불러오고, 수정하거나 변환하 는 데 사용됩니다.
데이터프레임(DataFrame)이라는 2차원 구조를 사용해 데이 터를 테이블 형식(행과 열)으로 다룹니다.
- numpy란 무엇인가?
고성능 다차원 배열 제공:
numpy.array는 리스트와 비슷하지만, 더 빠르고 메모리 효율적입니다.
다차원 데이터를 쉽게 처리할 수 있습니다(예: 2D 행렬, 3D 텐서).
벡터 연산 지원:
배열 간의 덧셈, 곱셈 같은 연산을 반복문 없이 빠르게 수행합니다.
수학 및 통계 기능 제공:
평균, 분산, 행렬 곱셈 등 고급 수학 연산을 지원합니다.
데이터 전처리:
정규화, 표준화, 차원 축소 등 데이터 변환을 효율적으로 수행할 수 있습니다.
+딥러닝 모델은 데이터를 다룰 때 주로 숫자로 이루어진 배열을 사용.
+ scikit-learn 머신러닝 모델을 쉽게 구현하고 평가할 수 있는 라이브러리
주요 기능
데이터 전처리 (Scaling, Encoding 등)
지도 학습 모델 (회귀, 분류)
비지도 학습 모델 (클러스터링, 차원 축소)
모델 선택 및 평가 (교차 검증, 성능 측정)
도구: 데이터 분할, 파이프라인 생성 등.
+ train_test_split은 데이터를 학습용 데이터(Training Set)와 테스트용 데이터(Test Set)로 분리하는 함수이다.
머신러닝 및 딥러닝에서 데이터를 나누는 것은 중요
reason
-> 학습 데이터는 모델의 가중치를 학습시키는 데 사용.
-> 테스트 데이터는 학습된 모델이 새로운 데이터에 대해 얼마나 잘 작동하는지 평가.
-> 학습 데이터와 테스트 데이터를 분리하지 않으면, 모델이 학습한 데이터로 평가하게 되어, 성능이 과대평가될 수 있음.
- data 전처리란 무엇인가?
데이터 전처리는 모델 학습에 적합하도록 데이터를 준비하는 과정입니다.
데이터를 정리하지 않으면 모델이 제대로 학습하지 못하거나 잘못된 결과를 도출할 수 있습니다.
- Dataset이란 무엇인가?
PyTorch의 Dataset은 모델 학습을 위한 데이터를 관리하는 도구입니다.
Dataset은 데이터를 저장하고, 특정 위치(인덱스)의 데이터를 반환하는 구조를 제공합니다왜 Dataset이 필요한가?
일반적인 데이터(예: NumPy 배열, Pandas DataFrame)는 모델 학습에 바로 사용할 수 없습니다. PyTorch 모델은 데이터를 Tensor(숫자의 배열) 형태로 받아야 하며, 이 데이터를 한 번에 처리할 수 있도록 관리하는 역할을 Dataset이 수행합니다.Dataset의 핵심 구조
init: 데이터를 초기화.
getitem: 특정 인덱스 데이터를 반환.
len: 데이터셋 크기 반환.
- DataLoader란 무엇인가?
PyTorch의 DataLoader는 Dataset으로부터 데이터를 배치(batch) 단위로 로드하는 도구입니다.
데이터를 한번에 모두 학습시키는 것이 아니라, 작은 묶음(배치)으로 나누어 처리하도록 도와줍니다.왜 DataLoader가 필요한가?
배치 단위 학습: 대량의 데이터를 한번에 모델에 입력하면 메모리 부족 문제가 발생할 수 있습니다.
데이터 셔플링: 데이터를 섞어서 학습 데이터의 편향을 방지합니다.
병렬 처리: 여러 코어를 사용해 데이터를 빠르게 로드합니다.
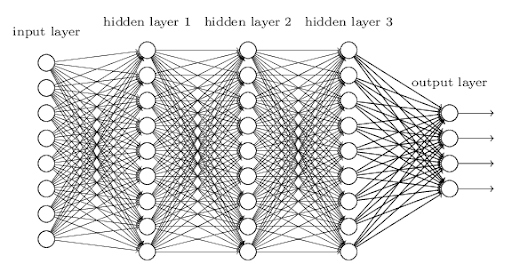
- MLP 모델 정의
하나 이상의 은닉층(hidden layer)을 가진 신경망이다. 각 층의 뉴런(노드)은 이전 층의 모든 노드와 연결된다(완전 연결층).
- MLP (다층 퍼셉트론, Multi-Layer Perceptron)
다층 퍼셉트론(MLP)은 인공 신경망(ANN)의 가장 기본적인 형태로, 입력 데이터에서 복잡한 패턴을 학습하기 위해 여러 개의 은닉층(hidden layers)을 사용합니다. 이를 통해 비선형 문제도 해결할 수 있습니다.
가중치와 바이어스:
각 연결은 학습 가능한 가중치(weight)와 바이어스(bias)를 가진다.
입력값에 가중치를 곱하고 바이어스를 더해 선형 변환을 수행한다.
이 과정에서 데이터의 패턴과 특징을 학습한다.가중치 행렬 (W):
입력 데이터와 출력 데이터 간의 관계를 학습하는 핵심 요소다. 다른 말로 하면 입력값이 출력값에 미치는 영향을 조정한다.
입력값에 곱해져 각 뉴런의 중요도를 조정한다.
학습을 통해 입력 특징의 중요도를 학습한다.바이어스 벡터 (b):
가중치 행렬만으로 설명되지 않는 데이터를 보정하는 역할을 한다.
뉴런의 출력값에 일정 값을 더해주는 역할을 한다.
데이터의 분포를 더 잘 맞추기 위한 일종의 보정 역할을 한다.초기값:
가중치 (W): 일반적으로 작은 난수로 초기화한다.
바이어스 (b): 일반적으로 0으로 초기화한다.업데이트 과정:
가중치와 바이어스는 역전파(Backpropagation)과정에서 손실 함수의 기울기를 기반으로 업데이트된다.
손실 계산 -> 기울기 계산 -> 가중치 및 바이어스 업데이트MLP구조:
입력층 (Input Layer): 모델에 데이터를 입력하는 층.
입력 데이터의 특징(feature) 개수만큼의 노드를 가집니다.
은닉층 (Hidden Layers): 입력 데이터를 처리하고, 복잡한 관계를 학습하는 중간 층.
여러 개의 은닉층을 쌓아 학습 성능을 높일 수 있습니다.
출력층 (Output Layer): 모델의 최종 출력(예: 분류 결과, 회귀값)을 생성하는 층.
출력 노드의 개수는 문제의 목표(클래스 개수, 회귀값)에 따라 달라집니다.MLP의 기본 특징
각 층은 완전히 연결(fully connected)된 구조로 이루어져 있습니다.
각 노드(neuron)는 가중치(weight)와 편향(bias)을 가지고, 입력 신호에 대해 계산을 수행합니다.
MLP 연산
z=W⋅x+b
W는 가중치, x는 입력, b는 편향입니다.활성화 함수 적용:
a=f(z)
비선형 활성화 함수를 사용해 복잡한 관계를 학습.
- 활성화 함수 (Activation Function)
활성화 함수는 뉴런이 출력 값을 결정하는 데 사용하는 비선형 함수입니다. 이를 통해 MLP는 단순한 선형 계산을 넘어 복잡한 문제를 학습할 수 있습니다.(음수 값을 0으로 변환 양수는 그대로 출력 함으로써 비선형성 부여)
활성화 함수의 역할
비선형성 추가: 데이터의 복잡한 패턴 학습 가능.
출력값 범위 제한: 모델 안정성과 학습 수렴 속도 향상.
ReLU (Rectified Linear Unit)
ReLU는 현재 가장 널리 사용되는 활성화 함수 중 하나입니다.
f(x)=max(0,x)
입력이 0보다 작으면 0을 반환하고, 0 이상이면 그대로 반환.특징:
계산이 간단하고 학습 속도가 빠름.
기울기 소실(Vanishing Gradient) 문제를 해결.
단점:
입력값이 계속 음수인 뉴런은 업데이트가 멈출 수 있음(죽은 ReLU 문제).
- 정규화 기법: 드롭아웃(Dropout)
드롭아웃은 과적합(overfitting)을 방지하기 위한 정규화 기법입니다. 학습 과정에서 일부 뉴런을 랜덤하게 비활성화(0으로 설정)하여 모델이 특정 뉴런에 의존하지 않고 일반화 성능을 향상시킵니다.
드롭아웃의 동작 방식
학습 시, 지정된 비율(예: 0.2)만큼의 뉴런을 랜덤하게 선택하여 비활성화.
테스트 시, 모든 뉴런을 활성화하되, 드롭아웃 비율을 고려해 출력값을 조정(가중치 스케일링).드롭아웃의 장점
특정 뉴런에 대한 과도한 의존 방지.
모델의 일반화 성능 향상.드롭아웃의 단점
학습 시간 증가: 랜덤 비활성화로 인해 매번 새로운 뉴런 구성을 학습.
적절한 드롭아웃 비율(보통 0.2~0.5)을 설정해야 함.
- 손실 함수와 최적화
손실 함수로 평균 제곱 오차(MSE), 최적화 알고리즘으로 Adam을 사용하여 모델의 학습 속도와 안정성을 높인다.
- 손실 함수(Loss Function): 평균 제곱 오차(MSE)
손실 함수란?
손실 함수는 모델의 예측값과 실제값의 차이를 측정합니다.
모델이 얼마나 잘 학습했는지 평가하며, 손실값을 줄이는 방향으로 학습이 진행됩니다.MSE (Mean Squared Error)
평균 제곱 오차는 회귀 문제에서 가장 많이 사용되는 손실 함수로, 예측값과 실제값 사이의 오차를 제곱한 값의 평균을 계산합니다.
yi = 실제값
yi^ = 모델의 예측값
n = 데이터 셈플의 개수특징
오차의 제곱:
오차를 제곱하므로 양수로 변환되어 오차의 크기를 강조.
큰 오차에 더 큰 페널티를 부여.
회귀 문제에 적합:
연속적인 값(예: 주택 가격, 온도 예측)에서 잘 작동.
- 최적화 알고리즘: Adam
최적화 알고리즘이란?
최적화 알고리즘은 손실 함수의 값을 최소화하기 위해 모델의 가중치와 편향을 업데이트하는 방법입니다. 경사 하강법(Gradient Descent) 기반의 다양한 변형 알고리즘이 있습니다.Adam (Adaptive Moment Estimation)
Adam은 학습 속도와 안정성을 높이기 위해 설계된 최적화 알고리즘입니다. 경사 하강법의 변형으로, 각 매개변수에 대해 모멘텀(momentum)과 적응 학습률(adaptive learning rate)을 활용합니다.Adam의 작동 방식
모멘텀 기반 업데이트:
이전 기울기를 활용해 매끄럽게 가중치를 업데이트.
빠른 수렴과 안정성을 제공.적응 학습률:
각 매개변수에 대해 학습률을 동적으로 조정.
자주 변화하는 매개변수는 작은 학습률을 사용하고, 천천히 변화하는 매개변수는 큰 학습률을 사용.Adam의 특징
장점:
학습률 조정 없이도 잘 작동.
빠르고 안정적으로 수렴.
희소 데이터 및 고차원 데이터에 적합.
단점:
매우 큰 데이터셋에서 가끔 과적합 발생.
- 모델 학습
에포크(epoch)와 배치(batch)를 기반으로 순전파와 역전파를 반복하며 모델의 가중치를 점진적으로 업데이트한다.
에포크(epoch)란?
정의: 에포크는 전체 데이터셋을 한 번 학습하는 과정을 의미합니다.
데이터를 모델에 여러 번 반복해서 학습시키기 위해 여러 에포크(epoch) 동안 학습을 진행합니다.
일반적으로 에포크가 많을수록 학습이 충분히 진행되지만, 너무 많으면 과적합(overfitting)이 발생할 수 있습니다.배치(batch)란?
정의: 배치는 데이터를 여러 개의 작은 묶음으로 나누는 것입니다.
배치 크기(batch size)는 한 번의 학습에서 모델에 입력되는 샘플의 개수를 뜻합니다.
데이터를 한 번에 모두 학습하지 않고, 배치 단위로 나누어 학습을 진행합니다.
배치 크기의 선택
소형 배치 (Batch size = 1): 한 번에 하나의 데이터만 학습 (온라인 학습).
대형 배치 (Batch size = 전체 데이터): 한 번에 모든 데이터를 학습 (배치 학습).
미니 배치 (Mini-batch, 보통 16~256):
소형과 대형의 절충안으로, 학습 속도와 안정성 간의 균형을 맞춤.순전파(Forward Propagation)
정의: 입력 데이터를 모델에 전달하여 예측값을 계산하는 과정.
역할:
모델이 입력 데이터를 통해 출력값(예측값)을 생성.
손실 함수에 예측값과 실제값을 비교해 손실(Loss)을 계산.
순서:
입력 데이터를 각 계층의 가중치와 편향으로 계산:z=W⋅x+b
활성화 함수 적용:a=f(z)
마지막 층에서 예측값 생성.역전파(Backward Propagation)
정의: 손실 값을 기반으로 모델의 가중치와 편향을 업데이트하기 위해 기울기(Gradient)를 계산하는 과정.
역할:
손실 함수의 값을 최소화하기 위해, 가중치에 대한 손실 함수의 미분값(기울기)을 계산.
가중치를 기울기의 반대 방향으로 업데이트(경사 하강법).
순서:
손실 함수로부터 시작해 출력층 → 은닉층 → 입력층 순으로 역방향으로 계산.
체인 룰(Chain Rule)을 사용해 각 가중치의 기울기 계산.
계산된 기울기를 사용해 가중치 업데이트.
-
에포크와 배치 기반 학습의 동작 과정
학습 단계
- 에포크 반복:
전체 데이터셋을 여러 번 반복 학습. - 배치 단위 학습:
데이터셋을 배치 크기만큼 나누어 처리. - 순전파(Forward Propagation):
각 배치를 모델에 입력하여 예측값 계산. - 손실 함수 계산:
예측값과 실제값을 비교해 손실 계산. - 역전파(Backward Propagation):
손실 값을 기반으로 각 가중치의 기울기를 계산. - 가중치 업데이트:
최적화 알고리즘(예: Adam, SGD)을 사용해 가중치 조정.
- 에포크 반복:
- 모델 평가
RMSE 지표를 통해 학습 데이터와 테스트 데이터에 대한 모델의 성능을 평가하고, 일반화 능력을 확인한다.