푸아송 분포

📍희귀한 사건이 발생할 때 사용하는 분포

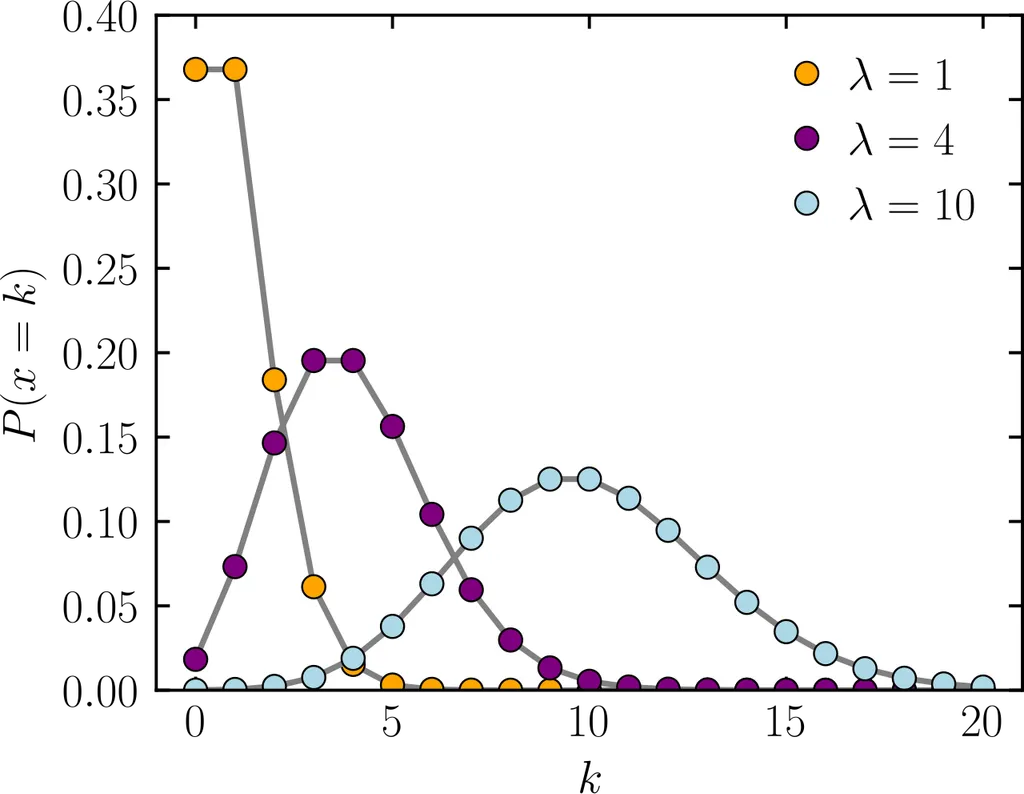
• 단위 시간 또는 단위 면적 당 발생하는 사건의 수를 모델링
• 평균 발생률 $\lambda$를 가진 사건이 주어진 시간 또는 공간 내에서 몇 번 발생하는지 나타냄.
• 이항분포와 마찬가지로 푸아송 분포도 이산형 분포
• 평균 발생률 $\lambda$가 충분히 크다면 정규분포에 근사.

📍 평균 발생률 $\lambda$: 주어진 시간이나 공간에서 사건이 몇 번 발생했는가?

• 단위 시간 또는 단위 면적 당 희귀하게 발생하는 사건의 수를 모델링할 때 적합.
  ex) 특정 시간 동안 콜센터에 도착하는 전화 통화 수
  ex) 특정 도로 구간에서 일정 기간 동안 발생하는 교통사고의 수
  ex) 특정 시간 동안 수신되는 문자 메시지의 수
  ex) 특정 시간 동안 웹사이트에 도달하는 방문자의 수

확률질량함수

$f(k;\lambda) = \frac{\lambda^ke^{-\lambda}}{k!}$

실습

• scipy.stats.poisson.pmf(사건 발생 홧수 범위, 람다) : 푸아송 분포 확률질량함수

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson

# 푸아송 분포 파라미터 설정
lambda_value = 4  # 평균 발생률
x = np.arange(0, 15)  # 사건 발생 횟수 범위 (x축 범위)

# 푸아송 분포 확률 질량 함수 계산
poisson_pmf = poisson.pmf(x, lambda_value)

# 그래프 그리기
plt.figure(figsize=(10, 6))
plt.bar(x, poisson_pmf, alpha=0.6, color='b', label=f'Poisson PMF (lambda={lambda_value})')
plt.xlabel('Number of Events')
plt.ylabel('Probability')
plt.title('Poisson Distribution')
plt.legend()
plt.grid(True)
plt.show()

+) 이항분포와의 관계? 람다(lambda, $\lambda$)란?

• 푸아송 분포의 평균(기댓값) $E(X)$와 $Var(X)$은 모두 $\lambda$로 동일하다.
• 이항분포에서 n이 매우 크고 p가 작은 경우에는 계산이 어렵다. 이 경우 극한값을 확용한 새로운 형태의 분포인 푸아송 분포를 통해 이항분포의 근사 확률을 구해 계산할 수 있다.
• 이항분포의 기댓값 $E(X)= \lambda=np$라고 하면, $p=\frac{\lambda}{n}$이라고 할 수 있다.

참고자료 1
참고자료 2