Scipy
- science + python의 의미
- 공학, 사회과학 등에서 자주 사용하는 기초통계 모듈과 함수를 모아놓은 라이브러리
자주 쓰는 함수
scipy
│
├── stats # 통계 분석과 확률 분포 관련 함수 제공
│ ├── norm # 정규분포 관련 함수 (PDF, CDF, 랜덤 샘플링 등)
| |── uniform * # 균등분포
| |── bernoulli * # 베르누이 분포
| |── binom * # 이항분포
│ ├── ttest_ind # 독립 두 표본에 대한 t-검정
│ ├── ttest_rel # 대응표본 t-검정
│ ├── mannwhitneyu # Mann-Whitney U 비모수 검정
│ ├── chi2_contingency # 카이제곱 독립성 검정
│ ├── shapiro # Shapiro-Wilk 정규성 검정
│ ├── kstest # Kolmogorov-Smirnov 검정 (분포 적합성 검정)
│ ├── probplot # Q-Q plot 생성 (정규성 시각화)
│ ├── pearsonr # Pearson 상관계수 계산
│ ├── spearmanr # Spearman 순위 상관계수 계산
│ └── describe # 기술 통계량 제공 (평균, 표준편차 등)- 대부분 'stats' 모듈 쪽에 분표 관련 함수들이 존재.
scipy.stats
scipy.stats.norm - SciPy v1.15.0 manual
- 주로 아래와 같이 불러온다
import scipy.stats as stats
scipy.stats.norm - 정규 분포
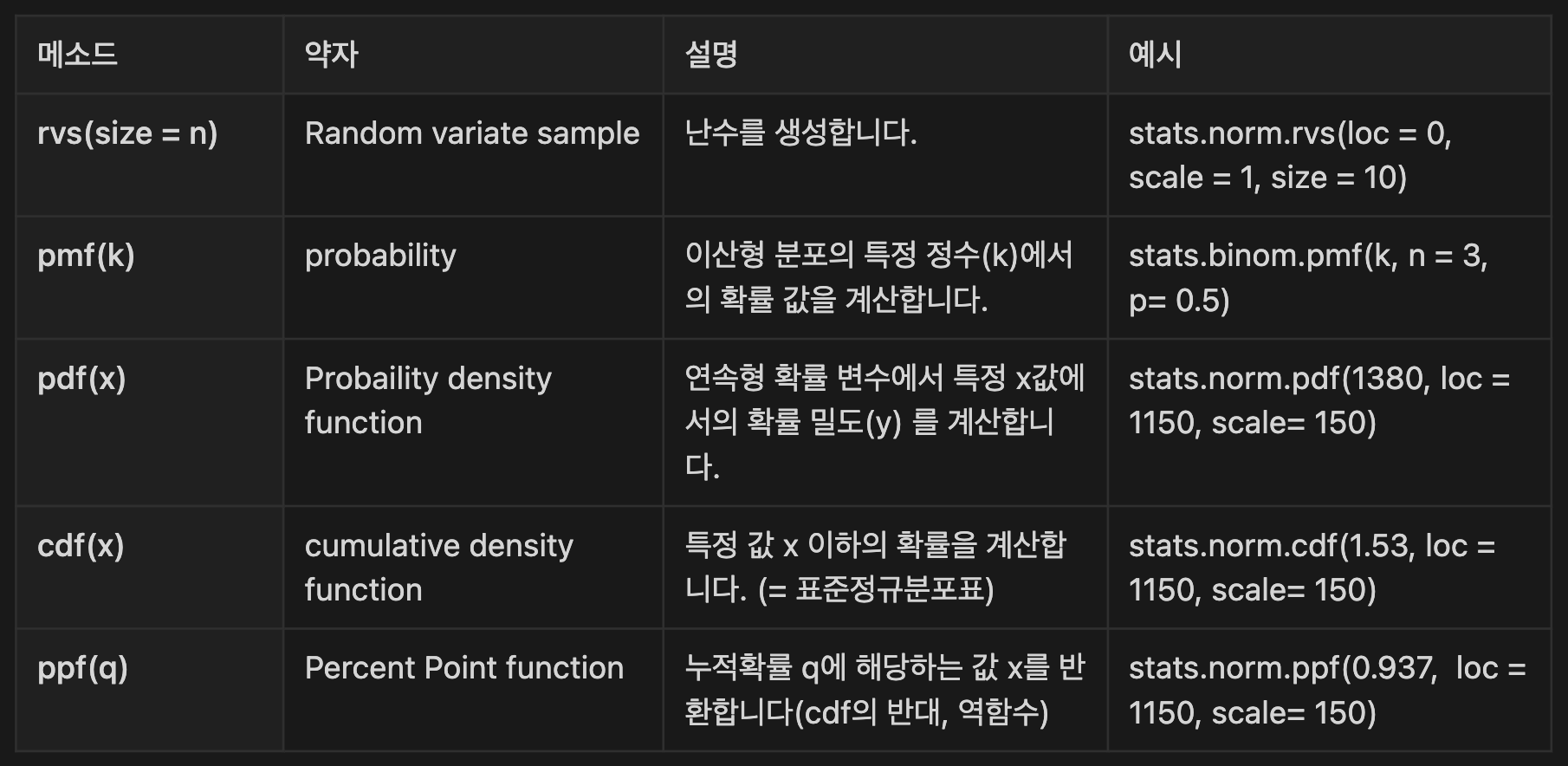
rvs: 난수 생성
scipy.stats.norm.rvs(loc, scale, size, random_state)- numpy의 random 모듈에 대응
- loc: 평균
- scale: 표준편차
- size: 생성할 데이터 개수
- random_state: 시드 설정
import scipy.stats as stats
import matplotlib.pyplot as plt
my_data = stats.norm.rvs(loc = 1150, scale = 150, size = 1000000)
plt.hist(my_data, bins = 100)
pdf: 특정 위치의 확률 구하기
scipy.stats.norm.pdf(x, loc, scale)- pdf = Probability Density Function, 즉, 확률밀도함수
- x: 확률을 구하고자 하는 x축 값
- loc: 평균
- scale: 표준편차
stats.norm.pdf(x = 1380, loc = 1150, scale = 150)
# 0.0008208834801723304- 평균이 1150, 표준편차가 150인 정규분포에서 '1380'일 확률 = 0.0008208834801723304
cdf: 누적 확률 분포 구하기
scipy.stats.norm.cdf(x, loc, scale)- cdf = Cumulative Density Function, 즉, 누적밀도함수
- pdf(확률밀도함수)의 적분값.
- x: 구하고자 하는 x축 값
- loc: 평균
- scale: 표준편차
stats.norm.cdf(x = 1380, loc = 1150, scale = 150)
# 0.9374031272090931- 평균이 1150, 표준편차가 150인 정규분포에서 '1380'는 백분율 93.74%
ppf: 백분율을 알 때 거꾸로 x 값 구하기
scipy.stats.norm.ppf(q, loc, scale)- ppf = Percent Point Function
- cdf의 역함수
- 평균이 loc이고, 표준편차가 scale인 정규분포에서 백분율이 q일 때, 확률변수가 몇인지 구함.
- q: 백분율
- loc: 평균
- scale: 표준편차
stats.norm.ppf(0.937, loc = 1150, scale = 150)
# 1379.5101382206744- 평균이 1150이고 표준편차가 150인 정규분포에서 백분율이 0.937에 해당하는 값은 1379.5101...
scipy.stats.uniform - 균등 분포
uniform.rvs(size, loc, scale)
- size: 반환할 개수
- loc: 0부터
- scale: 1 사이
from scipy.stats import uniform
# 균등 분포 생성 (예시: 0에서 1 사이)
uniform_dist = uniform.rvs(size=10, loc=0, scale=1)
# 결과 출력 (선택 사항)
uniform_dist결과:
array([0.83322308, 0.51922008, 0.02131206, 0.43868753, 0.00472524,
0.34721848, 0.23020302, 0.93142512, 0.83851749, 0.92177397])scipy.stats.bernoulli - 베르누이 분포
bernoulli.rvs(p, size)
- p: 확률
- size: 샘플 개수 (경우의 수)
from scipy.stats import bernoulli
# p는 성공 확률 (0과 1 사이)
p = 0.5
# size는 생성할 샘플의 개수
size = 10
# 베르누이 분포 샘플 생성
samples = bernoulli.rvs(p, size=size)
samples결과:
array([0, 0, 0, 1, 0, 1, 0, 0, 0, 0])scipy.stats.binom - 이항 분포
binom.pmf(k, p, n)
- pmf = Probability Density Function, 즉, 확률 밀도 함수
- 특정 값에서의 확률 계산
- k: 성공 횟수 (ex. 클릭한 유저가 2명인 경우)
- p: 성공 확률 (ex. 클릭을 할 확률)
- n: 시행 횟수 (ex. 3명의 유저)
from scipy.stats import binom
# n: 시행 횟수 (3명)
# p: 성공 확률 (클릭 확률, 0.5로 가정)
# k: 성공 횟수 (클릭한 유저 2명 나올 경우)
n = 3
p = 0.5
k = 2
# 이항 분포 확률 계산
probability = binom.pmf(k, n, p)
probability
# 결과: 0.3750000000000001