t 분포
- n이 30보다 충분히 큰 경우는 중심극한정리의 가정을 통해 모평균의 추론을 전개.
- 하지만 데이터의 수가 작은 경우에는 중심극한정리가 제한됨.
정의
- 모표준편차 를 알 수 없기 때문에 표본표준편차 로 대체
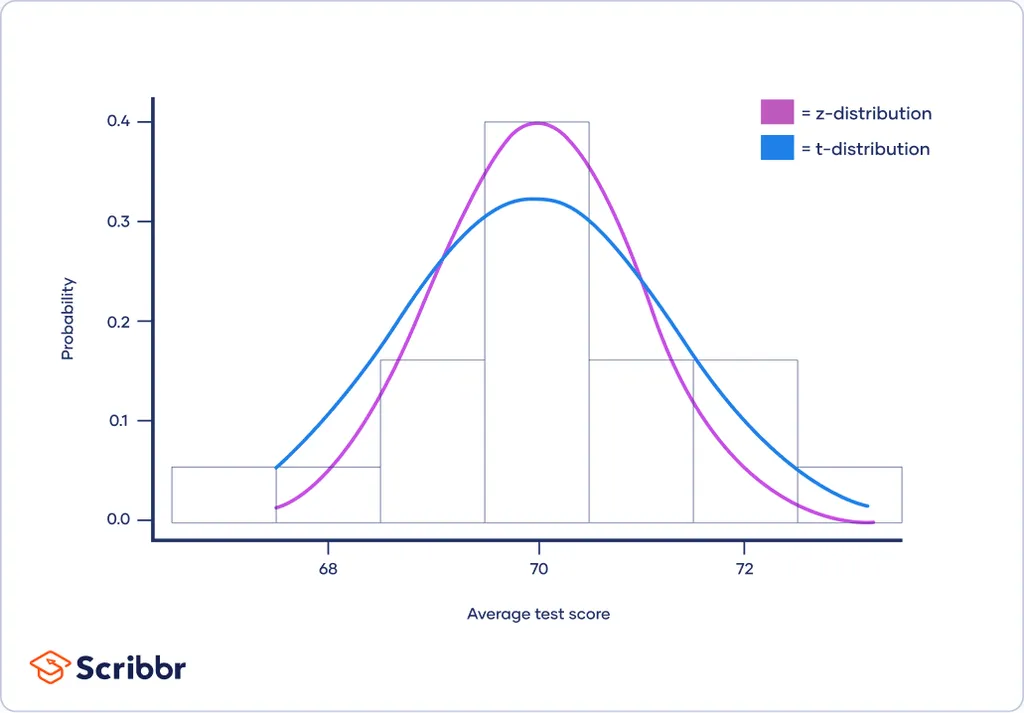
특징
- 표준정규분포처럼 평균 0을 기준으로 좌우대칭의 종모양
- 꼬리는 표준정규분포보다 두꺼움
- 자유도(degree of freedom)가 커짐에 따라 표준정규분포에 수렴함

자유도 degree of freedom
- 자유롭게 사용할 수 있는 데이터의 개수. 링크 참조!
- 모평균과 표본평균은 중심극한정리에 따라 매우 근사하여 대체 가능함
- 하지만 모표준편차와 표본표준편차는 구하는 공식이 완벽히 같지는 않다
- 모표준편차 - n으로 나눈다
- 표본표준편차 - n-1로 나눈다
예제 2) 전구의 수명시간 검정 (일표본 t검정)
Q. 한 회사에서 생산하는 전구의 평균 수명이 1000시간이라고 알려져 있습니다. 이 회사에서 생산된 전구 25개를 샘플링하여 전구의 평균 수명이 980시간이고, 표본 표준편차가 50시간이라고 할 때, 이 회사의 주장을 검증해보세요.
[요구사항]
1. 5%의 유의수준에서 t-검정을 수행하고, 귀무가설을 기각할 수 있는지 결정하세요.
2. t-통계량과 자유도를 계산하세요
3. p-value를 계산하고 이를 바탕으로 결론을 내세요.
- 가설 설정
- 귀무가설 : 전구의 평균 수명이 1000시간이다.
- 대립가설 : 전구의 평균 수명이 1000시간이 아니다.
- 표본 크기 = 25
- 표본 평균 = 1000
- 표본 표준편차 = 50
- 모평균 = 1000
- 유의수준
- t 통계량 계산
- 자유도: 25 - 1 = 24
- t = -2
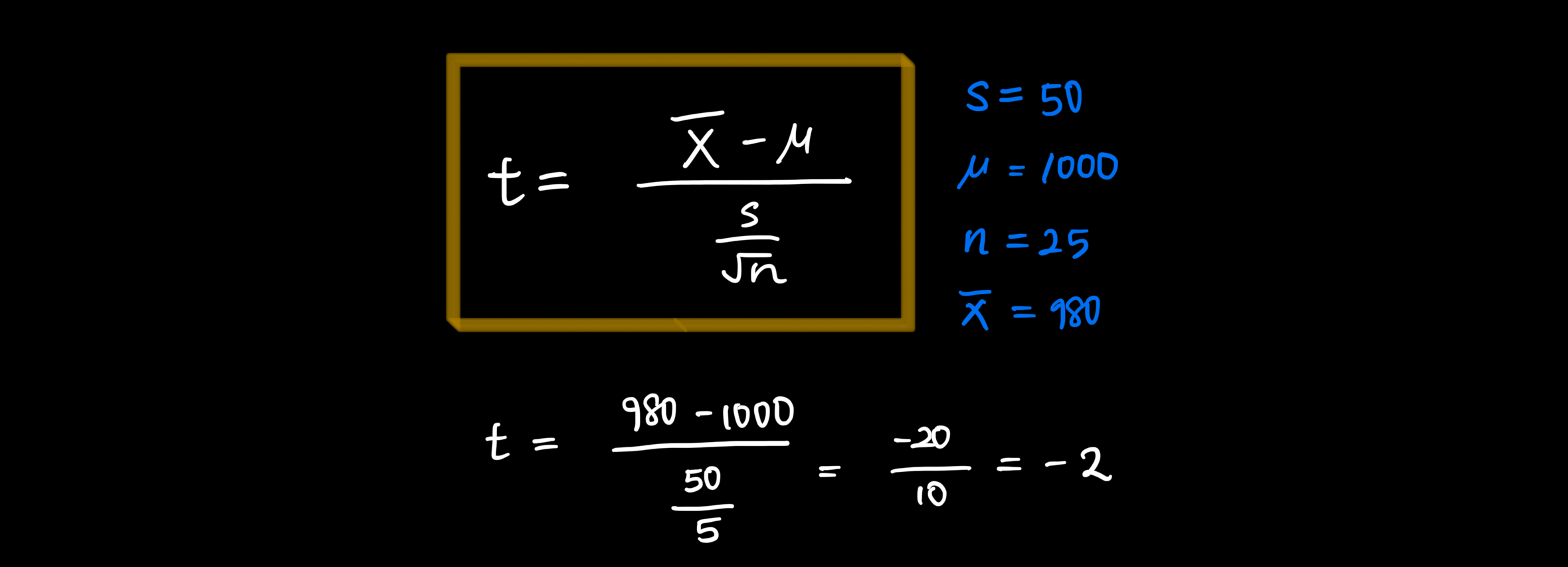
- p-value = 0.056
- 결론
- p-value > 0.05이므로 귀무가설 채택.
- 전구의 평균 수명은 1000시간이다.
실습 코드
import scipy.stats as stats
# 주어진 값들
n = 25 # 표본 크기
x_bar = 980 # 표본 평균
mu_0 = 1000 # 모집단 평균
s = 50 # 표본 표준편차
alpha = 0.05 # 유의수준
# t-통계량 계산
t_stat = (x_bar - mu_0) / (s / (n ** 0.5))
# 자유도 계산
df = n - 1
# p-value 계산
p_value = 2 * stats.t.cdf(-abs(t_stat), df)
# 결과 출력
print(t_stat, p_value)
alpha = 0.05
if p_value < alpha:
print("귀무가설을 기각합니다.전구의 평균수명은 1000시간이 아니다.")
else:
print("귀무가설을 기각하지 못합니다. 전구의 평균 수명은 1000시간 입니다.")결과:
-2.0 0.056939849936591666
귀무가설을 기각하지 못합니다. 전구의 평균 수명은 1000시간 입니다.
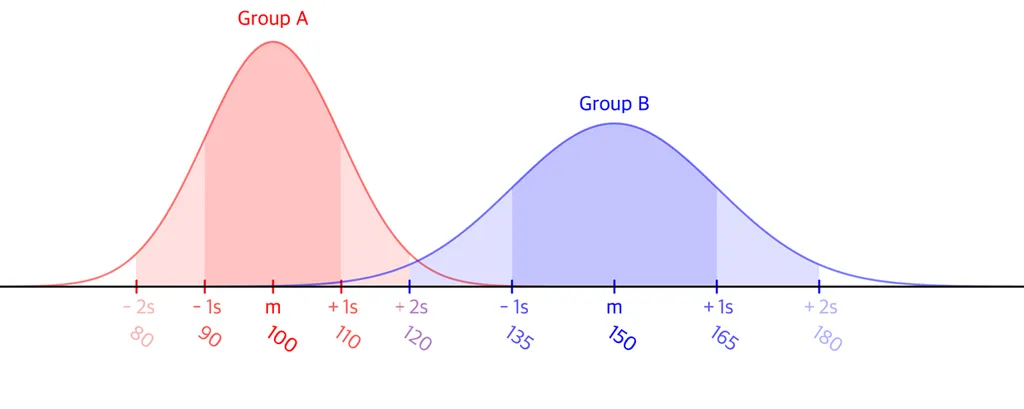
독립 표본 t 검정 (이표본 t검정)
- 두 표본 간 평균의 차이가 통계적으로 유의한지 확인
절차
-
각 표본에서 대응되는 값을 빼 차이를 정의.
-
차이 값의 평균과 표준편차를 구한다.
-
검정 통계량에도 적용시킨다.
다시 풀어쓰면
- 평균은 빼기
- 독립표본 t-검정은 두 집단의 평균 차이를 검정하기 위해 시행하는 것이기 때문! - 분산은 더하기
- 두 집단의 변동성을 나타내기 위해서!
예제 3) 전환율 비교
Q. 회사에서 두 가지 그룹에 대한 광고 캠페인을 진행했고, 전환율 데이터를 구했다. 유의수준 0.05에서 두 그룹의 전환율 데이터가 통계적으로 유의미한지 확인하라
- 가설 설정
- 귀무가설 : 두 그룹의 전환율에 차이가 없다.
- 대립가설 : 두 그룹의 전환율에 차이가 있다.
- 코드
import numpy as np
from scipy.stats import ttest_ind
# 그룹 A와 그룹 B의 전환율 데이터
group_a = np.array([0.045, 0.052, 0.048, 0.055, 0.049, 0.051, 0.047, 0.053, 0.050, 0.046,
0.054, 0.049, 0.052, 0.048, 0.055, 0.051, 0.047, 0.053, 0.050, 0.046,
0.054, 0.049, 0.052, 0.048, 0.055, 0.051, 0.047, 0.053, 0.050, 0.046])
group_b = np.array([0.056, 0.060, 0.052, 0.058, 0.054, 0.057, 0.053, 0.059, 0.056, 0.052,
0.061, 0.055, 0.058, 0.054, 0.060, 0.057, 0.053, 0.059, 0.056, 0.052,
0.061, 0.055, 0.058, 0.054, 0.060, 0.057, 0.053, 0.059, 0.056, 0.052])
# 독립 이표본 t-테스트 수행
t_stat, p_value = ttest_ind(group_a, group_b, equal_var=True) # 등분산 가정
# 결과 출력
print(f"t-통계량: {t_stat:.4f}")
print(f"p-value: {p_value:.4f}")
# 유의수준 설정
alpha = 0.05
if p_value < alpha:
print("귀무가설을 기각합니다. 두 그룹 간 평균에 통계적으로 유의미한 차이가 있습니다.")
else:
print("귀무가설을 기각하지 못합니다. 두 그룹 간 평균에 통계적으로 유의미한 차이가 있다는 증거가 부족합니다.")결과:
t-통계량: -7.9099
p-value: 0.0000
귀무가설을 기각합니다. 두 그룹 간 평균에 통계적으로 유의미한 차이가 있습니다.
