통계적 추론

가설검정의 용어

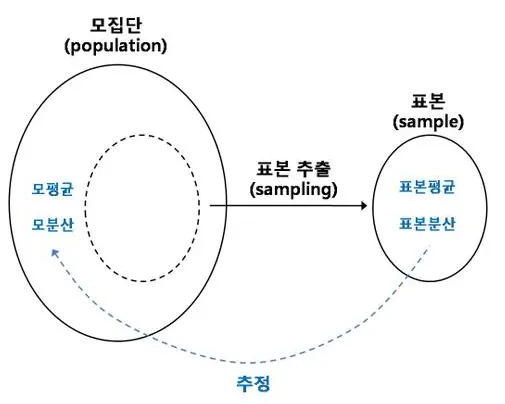
추정 Estimation

점 추정 Point Estimation

• 모수를 특정한 수치로 표현하는 것.
  ex) 남성의 평균 키는 170cm이다.

구간 추정 Interval Estimation

• 추정 값에 대한 신뢰도를 제시하면서 모수를 추정하는 방법.
  ex) 남성의 평균 키는 0~200cm이다. (정답이지만 명확하지 않음)
  남성의 평균 키는 16cm부터 177cm에 있을 확률이 95%이다. (구체적인 정보를 줌)
  

신뢰 구간 Confidential Interval

• 모수가 포함될 것이라고 예상되는 구간
• 전체 데이터 95%가 들어가 들어오는 구간을 많이 사용.

가설 검정 Hypothesis test

• 모집단의 특징에 대한 가설을 세우고 표본에서 얻는 정보를 통해 옳은지 판정하는 과정
  • 귀무가설 $H_0$: 현재 믿어지고 있는 가설. 실험과 연구를 통해 기각하고자 하는 가설
  • 대립가설 $H_1$: 새롭게 주장하는 가설

통계학은 일단 '귀무가설이 맞다'라고 생각하고, 이후에 모순이 발견되면 기존의 가정인 귀무가설을 기각하는 방식으로 증명 수행 $\rightarrow$ 귀류법, 반증법

이미지 출처

검정 통계량 Test Statistics

• 가설을 검정할 목적으로 정의하는 통계량
• 가설을 기각하는 지표.

ex) Z검정에 대한 검정 통계량

$Z=\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}$

$\frac{특정값 - 진리}{불확실성}$

표준 오차 Standard Error, SE, $\frac{\sigma}{\sqrt{n}}$

• 표본 평균 $\overline{X}$들의 표준편차
• 표본의 크기 n이 클수록, 표준 오차는 작아짐.
  • 더 많은 정보는 더 정확한 정보. 데이터를 많이 뽑을수록 오차가 줄어들테니까!
• 모표준편차$\sigma$가 작을수록, 표준오차는 작아짐.
  • 원본 데이터가 촘촘할수록 더 정확한 정보. 원본 자체가 편차가 적으니까!

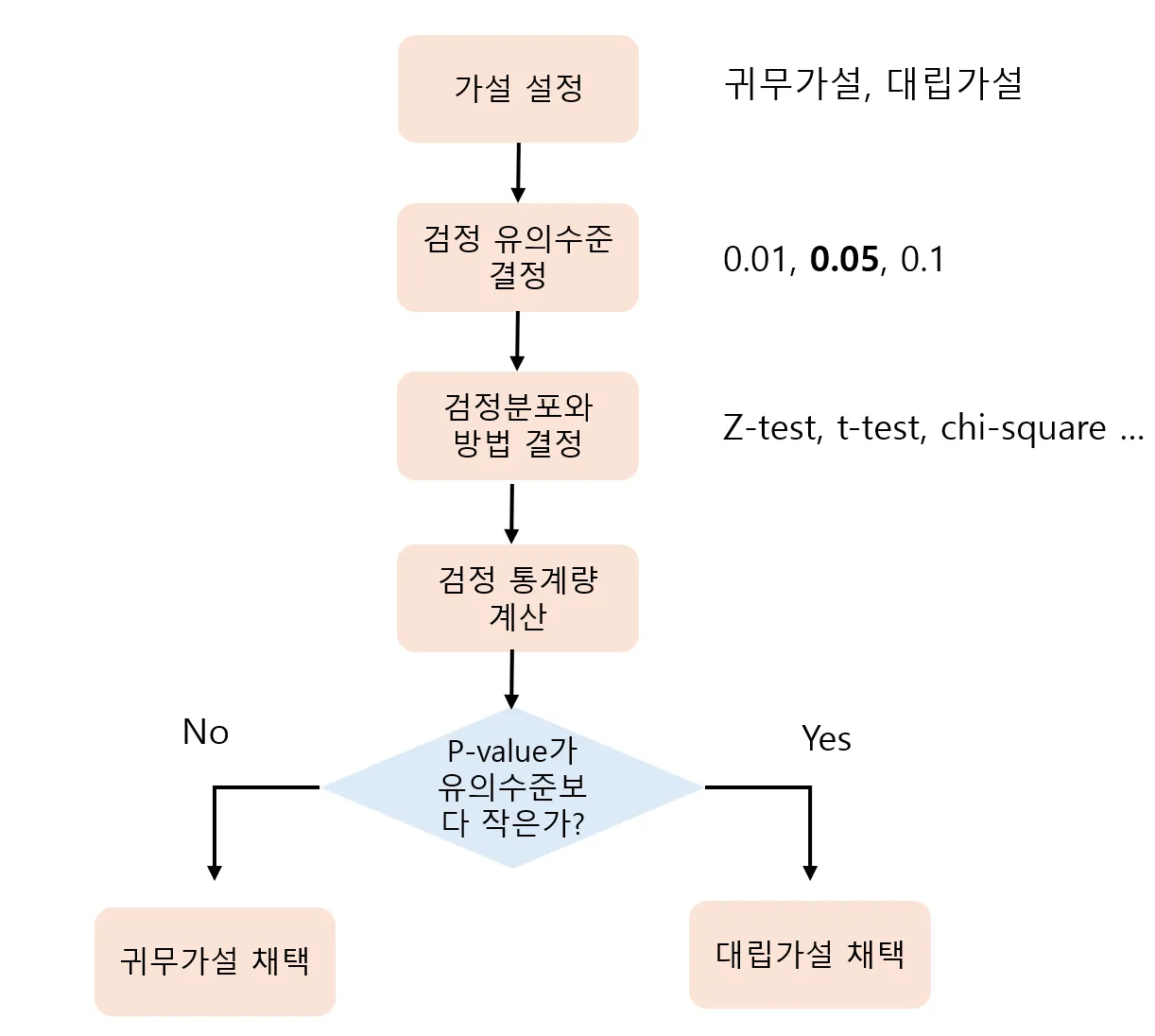
유의 수준 Sigmificant level, $\alpha$

• 귀무가설이 참임에도 잘못 기각할 오류를 범할 최대 허용 한계. (산업 표준 5%)
• 100번의 검증 중 5번은 틀릴 수 있다고 양해하고 관리하는 것.

p-value

• 귀무가설이 옳다고 가정할 때, 관측한 값(검정통계량)이 등장할 확률
• 만약 p-value < 0.05 (유의수준)이라면 귀무가설 기각, 대립가설 채택.
• 만약 p-value >= 0.05라면, 귀무가설 채택. 해당 결과는 우연에 의한 산물.

가설 설정 절차

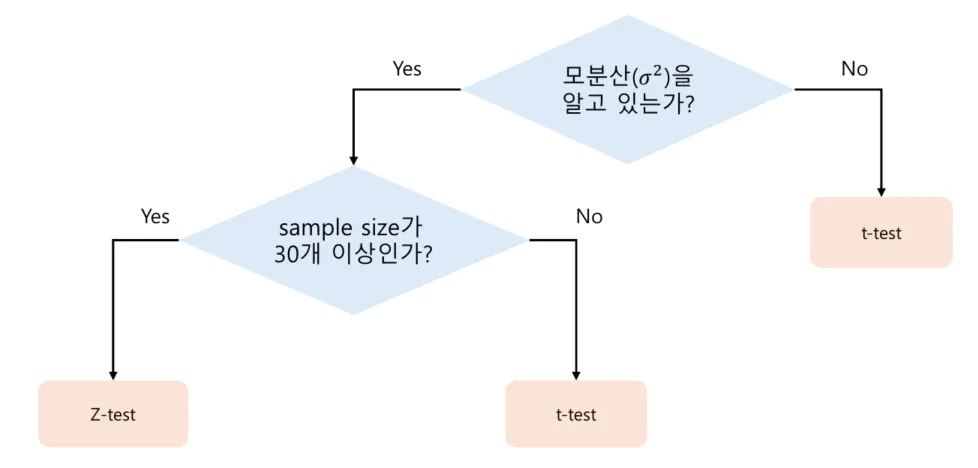
Z 검정 사용 조건

• 모집단의 표준편차 $\sigma$를 알고 있거나 표본의 크기가 충분히 클 때 (N > 30)
• 모집단이 정규분포임을 가정하고 검정.

예제 1) 고객 만족도 조사

• 한 회사의 고객 평균 만족도가 8점, 표준 편차는 1.5점으로 알려져있다.
• 새로운 서비스 도입 후 100명의 고객을 대상으로 표본 조사를 했더니 평균 만족도가 8.2점이 나왔다.
• 새로운 서비스로 인해 고객의 만족도가 유의미하게 달라졌는가? 유의수준 0.05를 기준으로 검정하라.

---

• $\mu=8$, $\sigma=1.5$ (모집단)
• $\overline{x}=8.2$

1. 가설 설정

• 귀무가설: $\mu=8$,고객의 만족도는 8이다.
• 대립가설: $\mu\neq8$,고객의 만족도는 8이 아니다.

2. 검정 유의수준을 0.05로 설정
3. 검정 분포: 모평균과 모표준편차가 알려져 있으므로 정규분포 사용
4. 검정 통계량 계산

   $Z=\frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}}$

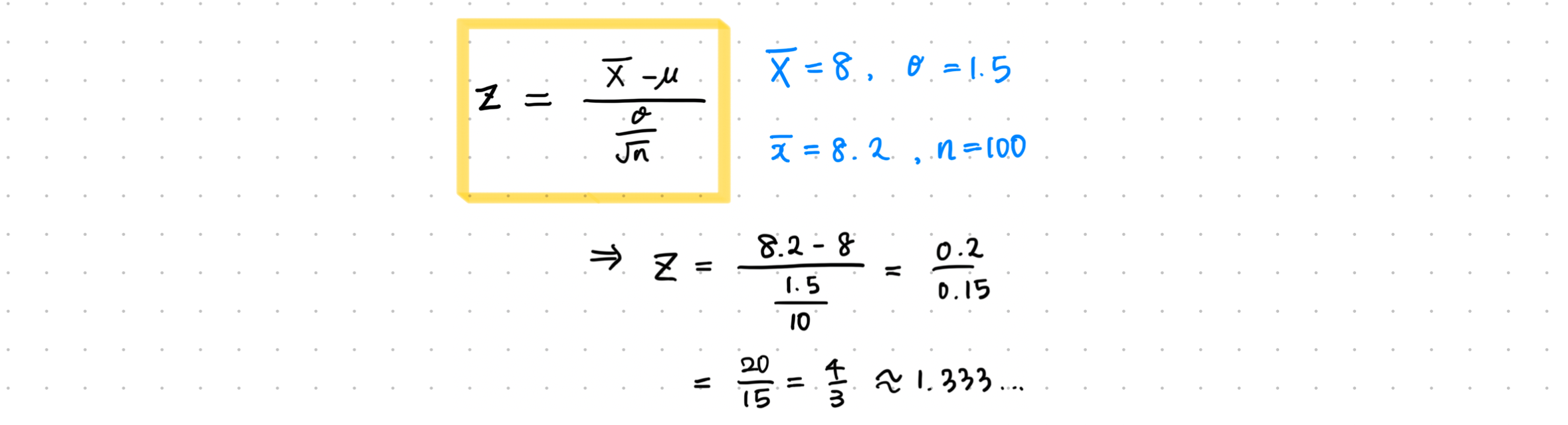
5. 결과 해석

• Z 검정 통계량은 1.33, p-value는 0.18
• p-value가 0.05보다 크기 때문에 귀무가설 채택.
• 즉, 새로운 서비스의 도입은 평균 만족도에 영향이 없다.

양측검정 vs 단측 검정

실습 코드

from scipy.stats import norm
import numpy as np

# 데이터 설정
mu_0 = 8  # 모집단 평균
sigma = 1.5  # 모집단 표준편차
n = 100  # 표본 크기
x_bar = 8.2  # 표본 평균

# 표준오차 계산
SE = sigma / np.sqrt(n)

# Z-통계량 계산
z_stat = (x_bar - mu_0) / SE

# 양측 검정 p-value 계산
p_value = 2 * (1 - norm.cdf(abs(z_stat))) # 확률밀도함수를 이용하여

# 결과 출력
print(f"Z-통계량: {z_stat:.2f}")
print(f"P-value: {p_value:.4f}")

# 유의수준 설정
alpha = 0.05
if p_value < alpha:
    print("귀무가설을 기각합니다. 새로운 정책이 만족도에 유의미한 영향을 미칩니다.")
else:
    print("귀무가설을 기각하지 못합니다. 새로운 정책이 만족도에 유의미한 영향을 미친다는 증거가 부족합니다.")

중심극한정리 Central Limit Theory, CTL

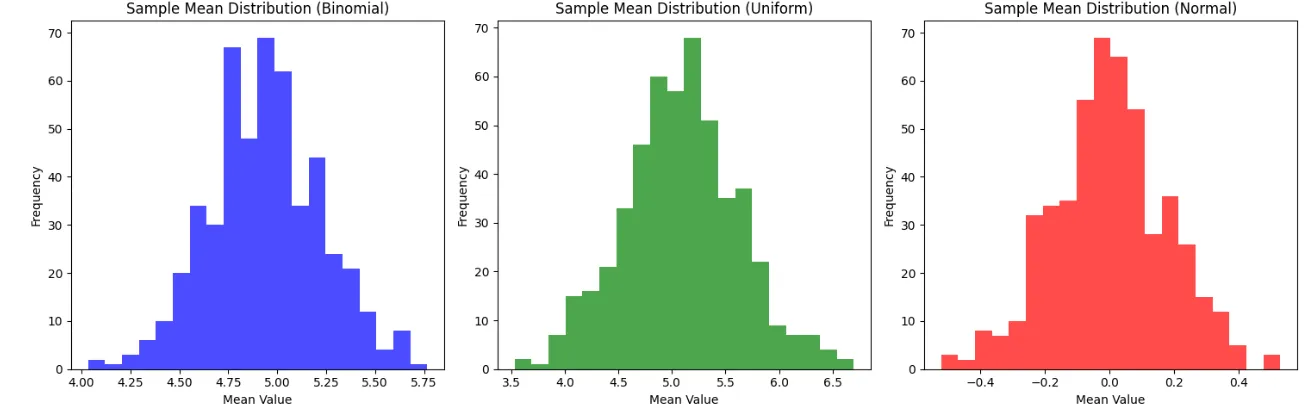
• 정규분포 모집단 $N(n, \sigma^2)$에서 뽑아낸 n개의 임의의 표본 평균 $\bar{X}$이 $n$과 같고, 표준편차는 $\frac{\sigma}{\sqrt{n}}$이다.
• n이 충분히 크다면 모집단의 분포에 상관 없이 표본 평균의 분포가 정규분포를 따른다는 것이 중심극한정리

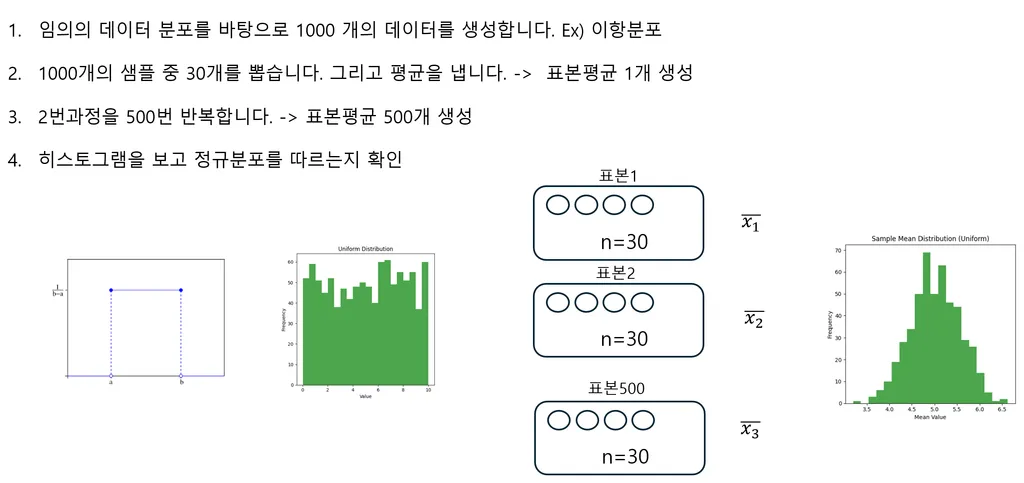
• 이를 이용하면 모집단에 대한 전수조사를 하지 않아도 표본들로부터 모평균에 근사할 수 있음

$\overline{X}\sim N(\mu, \frac{\sigma^2}{n})$

• 이때 표본 평균의 표준편차를 표준오차, Standard Error라고 함.

---

• 임의 생성한 모집단
  
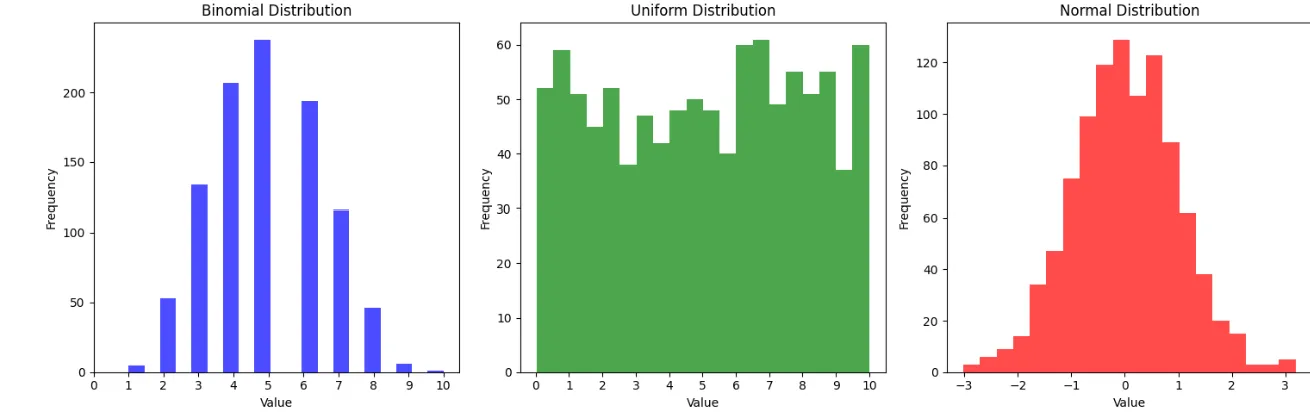
• 각 표본들의 평균