범주형 변수 분석 - one-way

범주형 변수는 어떻게 비교할까?

퇴직한 A씨는 상점을 매수하려는 상황입니다. 전 주인이 월~토에 대한 고객의 방문비율에 대한 정보를 전달했습니다. 이를 확인하고자 매일 실 고객을 세보았습니다. 전 주인이 말하는 비율이 맞을까요?

• 위 형태의 가설 검정을 적합도 검정 Goodness of fit이라고 함.
• 귀무가설 $H_0$: 요일별 방문객 수는 주장된 비율과 차이가 없다.
• 대립가설 $H_1$: 요일별 방문객 수는 주장된 비율과 차이가 있다. 다르다!

	월	화	수	목	금	토	합계
주장하는 방문 비율 (%)	10	10	15	20	30	15	100
관측한 방문 수 (명)	30	14	34	45	57	20	200

카이제곱 검정 $\chi^2$

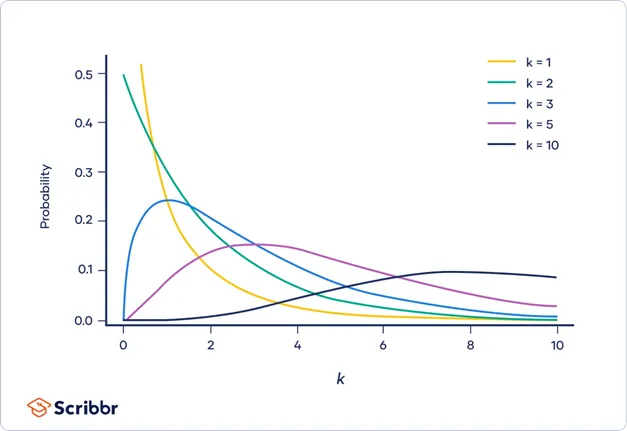
• 위 예제와 같은 횟수 검정에 사용하기 위해 고안된 분포
• 카이제곱 분포는 표준정규분포 확률 변수의 제곱합으로 정의

$\sum_{i=1}^{n}Z_{i}^{2} = \sum_{i=1}^{n}[\frac{X_i-\mu}{\sigma}] = \chi^2$

• 관측한 것에 비해 얼마나 맞았는가를 측정하기 위해서 다음의 검정 통계량 제시

$\chi^2 = \sum\frac{(O-E)^2}{E}$

• $O$: 관측 도수. Observed.
• $E$: 기대 도수. Expected.

분자는 관측한 값이 얼마나 떨어져있냐에 대한 지표이고 -값도 존재할 수 있으니 제곱으로 모두 양수로 바꾼다.
그리고 크기를 보정시켜주기 위해서 분자를 기대값으로 한번 나눠준다.

적합도 검정 Goodness of fit

	월	화	수	목	금	토	합계
주장하는 방문 비율 (%)	10	10	15	20	30	16	100
관측한 방문 수 (명)	30	14	34	45	57	20	200
(주장에 따른) 기대 방문 수 (명)	20	20	30	40	60	30	200
계산식	200 * 0.1	200 * 0.1	200 * 0.15	200 * 0.2	200 * 0.3	200 * 0.15	200

$\chi^2 = \\\,\\\frac{(30-20)^2}{20} + \frac{(14-20)^2}{20} + \frac{(34-30)^2}{30} + \frac{(45-40)^2}{40} + \frac{(57-60)^2}{60} + \frac{(20-30)^2}{30} \\\,\\= 11.442$

• 월~토 데이터 개수는 6개
• 카이제곱은 n-1의 자유로에 따르기 때문에 자유도는 5
• 자유도 5인 카이제곱 분포와 검정 통계량 시각화

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2

# 자유도 설정
df = 5

# 카이제곱 분포 범위 생성
x = np.linspace(0, 20, 500)
y = chi2.pdf(x, df)

# 카이제곱 검정 통계량
chi2_stat = 11.442

# 그래프 그리기
plt.figure(figsize=(8, 5))
plt.plot(x, y, label=f'Chi-Square Distribution (df={df})', color='blue')
plt.axvline(x=chi2_stat, color='red', linestyle='--', label=f'Chi-Square Stat = {chi2_stat}')
plt.title('Chi-Square Distribution and Test Statistic', fontsize=14)
plt.xlabel('x', fontsize=12)
plt.ylabel('Probability Density', fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
plt.show()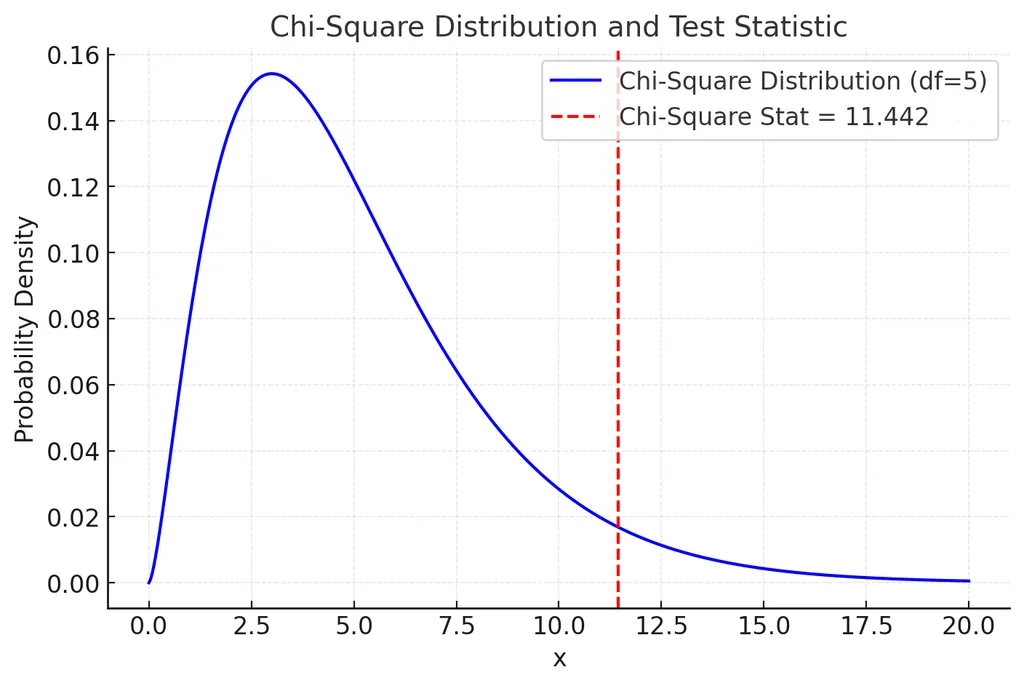

적합도 검정

• scipy.stats.chisquare(f_obs, f_exp, ddof)
  • f_obs: 관측된 값 (개수)
  • f_exp: 기대값
  • ddof: 자유도. 전체 범주 개수 - 1
• 리턴값
  - statistic: 카이제곱 통계량
  • p-value

# 주장하는 방문 비율(%)을 기반으로 기대값을 계산
expected_ratios = np.array([10, 10, 15, 20, 30, 15])
total_visits = 200
expected_counts = (expected_ratios / 100) * total_visits

# 관찰된 방문 수
observed_counts = np.array([30, 14, 34, 45, 57, 20])

# 카이제곱 적합도 검정을 수행
chi2_stat, p_val = stats.chisquare(f_obs=observed_counts, f_exp=expected_counts)

# 결과 출력
print(f"Chi-squared Statistic: {chi2_stat:.3f}") # 11.442
print(f"P-value: {p_val:.3f}") # 0.043

# 결론 도출
alpha = 0.05  # 유의수준
if p_val < alpha:
    print("귀무가설 기각: 관찰된 방문 비율은 주장하는 비율과 다르다.")
else:
    print("귀무가설 채택: 관찰된 방문 비율은 주장하는 비율과 같다.")
   

결과:

Chi-squared Statistic: 11.442
P-value: 0.043
귀무가설 기각: 관찰된 방문 비율은 주장하는 비율과 다르다.

+)

카이제곱 검정은 비모수 검정, 즉 정규분포가 아니더라도 가능한 검정.
단, 각 카테고리의 빈도수가 5를 넘어야함.
5가 넘지 않으면 피셔의 정확 검정 (exact test)을 수행해야 함.

범주형 변수 분석 - two-way

• 카이제곱의 세 가지 검정 방법
  • 적합도 검정: 1차원 데이터
  • 독립성 검정: 2차원 데이터
  • 동질성 검정: 2차원 데이터

독립성 검정 Test of Independence

두 변수의 독립유무를 확인하는 과정

예시) 흡연과 성별 사이에 관계가 있을까?

• $H_0$: 흡연과 성별은 독립적이다.
• $H_1$: 흡연과 성별은 독립적이지 않다.

귀무가설과 대립가설 설정에 의문을 가질 수 있지만, 세상에 랜덤한 어떤 변수를 갖다대었을 때 두 변수는 독립적일 경우가 훨씬 많다.

	흡연	비흡연	합계
남성	40	60	100
여성	30	70	100
합계	70	130	200

• 흡연의 기댓값: 35
• 비흡연 기댓값: 65

관측(기대)	흡연	비흡연	합계
남성	40(35)	60(65)	100
여성	30(35)	70(65)	100
합계	70	130	200

• 카이제곱 통계량

  $\chi^2 = \frac{(40-35)^2}{35} + \frac{(30-35)^2}{35} + \frac{(60-65)^2}{65} + \frac{(70-65)^2}{55} = 2.1978$

• 자유도: 2차원이기 때문에 (행의 수 - 1) * (열의 수 - 1) = 1

• p-value 결과 = 0.138로, 0.05보다 크기 때문에 귀무가설을 기각하지 못함.

• 즉, 성별과 흡연의 관계는 독립적이다.

코드

# 관찰된 데이터: 성별과 흡연 여부에 따른 빈도수
data = np.array([
    [40, 60],  # 남성: 흡연자, 비흡연자
    [30, 70]   # 여성: 흡연자, 비흡연자
])

# 카이제곱 통계량, p-value, 자유도, 기대값을 계산
chi2_stat, p_val, dof, expected = stats.chi2_contingency(data, correction=True)

# 결과 출력
print(f"Chi-squared Statistic: {chi2_stat:.3f}") #1.780
print(f"P-value: {p_val:.3f}") #0.182
print(f"Degrees of Freedom: {dof:.3f}") #1.000
print("Expected frequencies:")
print(expected)

# 결과:
[[35. 65.]
 [35. 65.]]


# 결론
alpha = 0.05  # 유의수준
if p_val < alpha:
    print("귀무가설 기각: 성별과 흡연 여부는 독립적이지 않다.")
else:
    print("귀무가설 채택: 성별과 흡연 여부는 독립적이다.")

Chi-squared Statistic: 1.780
P-value: 0.182
Degrees of Freedom: 1.000
Expected frequencies:
[[35. 65.]
[35. 65.]]
귀무가설 채택: 성별과 흡연 여부는 독립적이다.

동질성 검정 Test of Homogeneity

두 집단의 분포가 동일한지 확인

예시) 학교별 과목 선호도가 같을까?

• $H_0$: 각 학교의 과목별 선호도는 동일하다.
• $H_1$: 각 학교의 과목 선호도는 동일하지 않다. 다르다!

과목	학교A	학교B	학교C	합계
수학	50	60	55	165
과학	40	45	50	135
문학	30	35	40	105
합계	120	140	145	405

• 기대값 계산

  학교 전체의 수학:과학:분학 선호도 비율 = 165:135:105
  각 학교의 합계를 위 비율로 나누면 학교별 해당 과목의 기댓값을 구할 수 있음
  예) 학교 A의 수학 선호도 기대값 = 120 * (165/405) = 48.888...

관측수(기대값)	학교A	학교B	학교C	합계
수학	50(48.89)	60(57.04)	55(59.07)	165
과학	40(40.0)	45(46.67)	50(48.33)	135
문학	30(31.11)	35(36.30)	40(37.60)	105
합계	120	140	145	405

• 자유도: (3-1) * (3-1) = 4
• 카이제곱 통계량: 0.817
• p-value: 0.936으로 0.05보다 크기 때문에 귀무가설 기각하지 못함.
• 즉, 각 학교의 과목 선호도는 동일하다.

코드

# 관찰된 데이터: 각 학교에서 학생들이 선호하는 과목의 빈도수
data = np.array([
    [50, 60, 55],  # 수학 선호
    [40, 45, 50],  # 과학 선호
    [30, 35, 40]   # 문학 선호
])

# 카이제곱 통계량, p-value, 자유도, 기대값을 계산
chi2_stat, p_val, dof, expected = stats.chi2_contingency(data)

# 결과 출력
print(f"Chi-squared Statistic: {chi2_stat:.3f}")# 0.817
print(f"P-value: {p_val:.3f}") # 0.936
print(f"Degrees of Freedom: {dof:.3f}") # 0.400
print("Expected frequencies:")
print(expected.round(3))

'''
[[48.889 57.037 59.074]
 [40.    46.667 48.333]
 [31.111 36.296 37.593]]
'''

# 결론
alpha = 0.05  # 유의수준
if p_val < alpha:
    print("귀무가설 기각: 각 학교에서 과목 선호도는 동일하지 않다.")
else:
    print("귀무가설 채택: 각 학교에서 과목 선호도는 동일하다.")

결과:

Chi-squared Statistic: 0.817
P-value: 0.936
Degrees of Freedom: 4.000
Expected frequencies:
[[48.889 57.037 59.074]
[40. 46.667 48.333]
[31.111 36.296 37.593]]
귀무가설 채택: 각 학교에서 과목 선호도는 동일하다.

독립성 검정과 동질성 검정의 차이

• 모두 chisquare 검정 진행
• 검정의 목적과 해석의 차이가 존재

	독립성 검정	동질성 검정
공통점	카이제곱 검정	카이제곱 검정
목적	두 범주형 변수 간 독립성 여부	여러 집단의 분포가 동일한지 검정
가설	$H_0$: 두 변수는 독립적이다. $H_1$: 두 변수는 독립적이지 않다.	$H_0$: 두 변수는 분포가 동일하다. $H_1$: 두 변수는 분포가 동일하지 않다.