검정과 오류

새로운 고혈압약을 개발하는 제약사가 있습니다. 식약처는 국민의 건강을 고려하여 승인을 해야합니다. 고혈압을 개발한 제약사는 자신들의 개발한 약이 엄청난 효과가 있다라고 주장하지만 글쎄? 이 과정에서 일어 날 수 있는 통계적 오류에 대해서 알아봅시다.

• 식약처는 엄격한 허가 과정이 필요하므로 다음과 같이 가설을 설정
  • 귀무가설($H_0$): 고혈압 약이 효과가 없음
  • 대립가설($H_1$): 고혈압 약이 효과가 있음(제약사가 주장하는 가설)

• 만약 아주 엄격한 기준으로 약을 허가한다면 -> 국민들의 편익이 적음
  • 허가받을 수 있는 약이 적어짐!
• 만약 널널한 기준으로 약을 허가한다면 -> 국민들에게 위해가 될 수 있음
  • 효과가 없는 약이 유통될 수 있음!

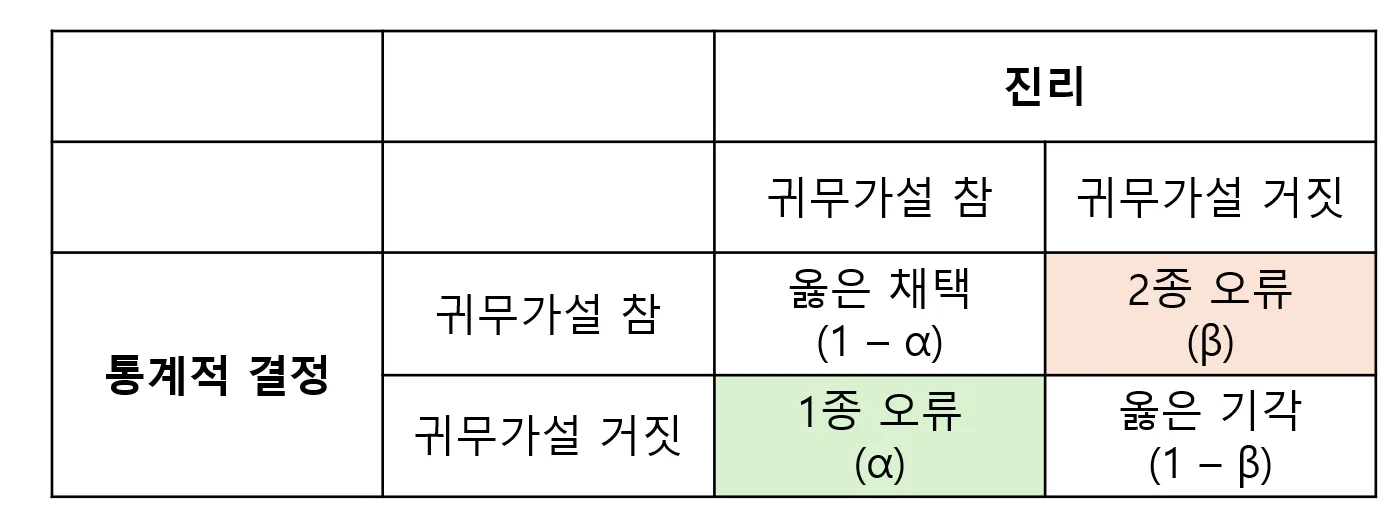
• Case 1 - 1종 오류 $\alpha$
  • 귀무가설이 참인데도 귀무가설을 기각하고 대립가설을 채택하는 경우
  • ex) 고혈압 약이 효과가 없는데도 있는 것으로 판단.
  • 국민들의 위해가 우려되는 상황.

• Case 2 - 2종 오류 $\beta$
  • 귀무가설이 거짓이라 기각해야 하는데 귀무가설을 채택하는 경우
  • ex) 고혈압 약이 효과가 있는데 없다고 하는 경우.

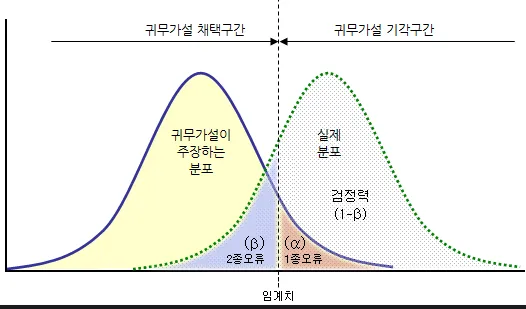
• 옳게 판단할 영역인 $1-\beta$를 검정력이라고 부르며, A/B 테스트에서 중요하게 다룸
• 실제로는 1종 오류가 더 큰 위험이라고 판단하기 때문에 이를 유의수준으로 정의하고 관리

데이터 분석에서의 검정 절차

현실 세계에서는 모집단이 정규성을 따른다는 가정을 확인하기 어려울 수 있습니다. 이런 상황에서 적용할 수 있는 비모수적 방법을 포함한 절차를 알아봅시다.

검정의 가정

• Z 검정과 T 검정 모두 데이터가 정규 분포를 따른다는 가정이 있음
• 이를 모수적 검정 (parametric 검정)이라 함

Z 검정

• 모집단의 분산 혹은 표준편차를 알고 있음
• 표본의 크기가 충분히 커야 함 (N >= 30)
• 데이터가 정규 분포를 따라야 함

t 검정

• 모집단의 분산을 알지 못함
• 표본의 크기가 충분히 크지 않음 (N < 30)
• 데이터가 정규 분포를 따라야 함

2표본 검정 절차

• 그룹이 2개인 경우 대응 표본인지 확인
  • 정규분포를 따르는지 확인 (ex. Shapiro 검정) - 모집단이 정규분포를 따르는지 확인하기 위해
  • 등분산성 확인 (ex. levene 검정)

실습

정규성 검정

• $H_0$: 데이터가 정규 분포를 따른다.
• $H_1$: 데이터가 정규 분포를 따르지 않는다.

1. shapiro-wilk: 작은 표본에 적합
2. Kolmogorov-Smirnov: 표본이 클 때 (N >= 50)

# 정규성 검정 - Shapiro-Wilk
from scipy.stats import shapiro
statistic, p_value = shapiro(data)

# 정규성 검정 - Kolmogorov-Smirnov 검정 
from scipy.stats import kstest
statistic, p_value = kstest(data, 'norm')

print(f"Test Statistic: {statistic}")
print(f"p-value: {p_value}")

if p_value > alpha:
    print("정규성을 따른다고 볼 수 있습니다.")
else:
    print("정규성을 따른다고 볼 수 없습니다.")

등분산 검정

• $H_0$: 두 집단의 분산이 같다.
• $H_1$: 두 집단의 분산이 다르다.

1. Levene: 여러 그룹의 분산이 동일한지 검정. 정규성 검정 불필요.
2. Bartlett: 데이터가 정규 분포를 따른다는 가정. 정규성이 만족될 때 Levene보다 검정력 높음

from scipy.stats import levene, bartlett, fligner

statistic, p_value = levene(data1, data2)

# statistic, p_value = bartlett(data1, data2)
# statistic, p_value = fligner(data1, data2)