표본 오차 Sampling Error
- 표본에서 계산된 통계량과 모집단의 진짜 값 사이의 차이
- 표본의 크기가 클수록 표본 오차는 작아짐.
- 표본이 모집단을 완벽하게 대표하지 못하기 때문에 발생.
- 표본의 크기와 표본 추출 방법 등에 따라 달라질 수 있음.
- 표본의 크기: 클수록 표본 오차는 줄어든다. 더 많은 데이터를 수집할수록 모집단을 더 잘 대표한다.
- 표본 추출 방법: 무작위 추출 방법을 사용하면 표본 오차를 줄일 수 있다. 모든 모집단의 요소가 선택될 기회를 동등하게 가지도록 해야 한다.
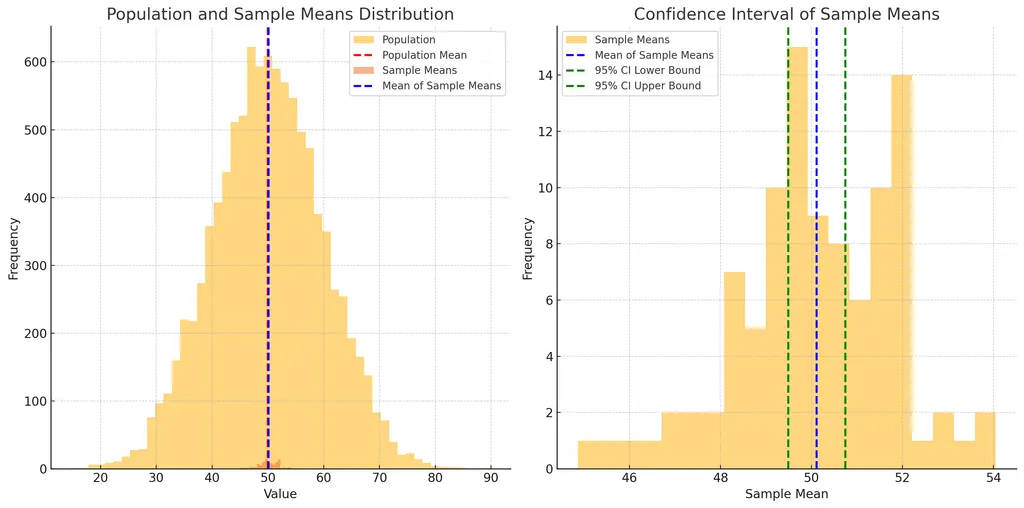
신뢰구간 Confidence Interval
- 모집단의 특정 파라미터(평균, 비율 등)에 대한 추정된 값이 포함될 것으로 기대되는 범위.
- 계산 방법
- 신뢰구간 = 표본 평균 z * 표준 오차
- z는 선택된 신뢰 수준에 해당하는 z값.
- ex) 95% 신뢰수준의 z값은 1.96
- 일반적으로 95% 신뢰수준을 많이 사용.
실습
import scipy.stats as stats
# 표본 평균과 표본 표준편차 계산
sample_mean = np.mean(sample)
sample_std = np.std(sample)
# 95% 신뢰구간 계산
conf_interval = stats.t.interval(0.95, len(sample)-1, loc=sample_mean, scale=sample_std/np.sqrt(len(sample)))
print(f"표본 평균: {sample_mean}")
print(f"95% 신뢰구간: {conf_interval}")결과:
표본 평균: 170.22077103284354
95% 신뢰구간: (168.10640026634232, 172.33514179934477)scipy.stats.t.interval(alpha, df, loc=0, scale=1)
- (추후 공부할) t 분포를 사용하여 신뢰구간을 계산.
- alpha: 신뢰 수준. 만약 95% 신뢰구간을 원한다면 alpha = 0.95
- df: 자유도. 일반적으로 표본 크기에서 1을 뺀 값. df = n-1
- loc: 표본의 평균
- scale: 표본의 표준 오차. 표본 평균들의 편차. 모집단의 표준편차()를 표본 크기의 제곱근으로 나눈 값. scale = sample_std/sqrt(n)
