다항회귀
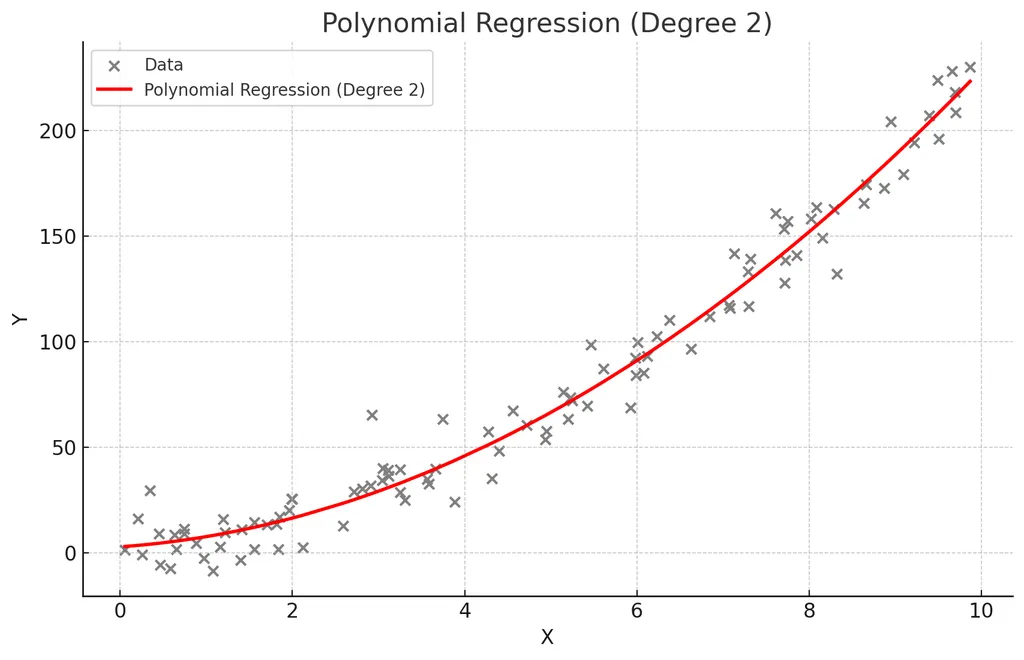
- 독립 변수와 종속 변수간의 관계가 선형이 아닐 때, 독립 변수에 다항식을 사용하여 종속 변수 예측
- 데이터가 곡선적 경향을 따를 때 사용.
- 비선형 관계를 모델링
- 고차 다항식의 경우 과적합(overfitting)의 위험이 있음.
스플라인 회귀
- 독립 변수의 구간별로 다른 회귀식을 적용하여 복잡한 관계를 모델링
- 구간마다 다른 다항식을 사용하여 전체적으로 매끄러운 곡선을 생성
- 데이터가 국부적으로 다른 패턴을 보일 때 사용
- 복잡한 비선형 관계를 유연하게 모델링
- 적절한 매듭점(knots) 선택이 중요

실습
- np.newaxis: 1D array를 row vector나 column vector로 사용하도록
참고자료 - PolynomialFeatures(degree): 기본 다항식 형태 만들기
- fit_transform(data): 데이터를 다항 형태로 변형
from sklearn.preprocessing import PolynomialFeatures
# 예시 데이터 생성
np.random.seed(0)
X = 2 - 3 * np.random.normal(0, 1, 100) # X.shape = (100,)
y = X - 2 * (X ** 2) + np.random.normal(-3, 3, 100)
X = X[:, np.newaxis] # X.shape = (100,1)
# 다항 회귀 (2차)
polynomial_features = PolynomialFeatures(degree=2) # 다항식 형태
X_poly = polynomial_features.fit_transform(X) # 데이터 X를 다하익 형태로 변형
model = LinearRegression()
model.fit(X_poly, y)
y_poly_pred = model.predict(X_poly)
# 모델 평가
mse = mean_squared_error(y, y_poly_pred)
r2 = r2_score(y, y_poly_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)
# 시각화
plt.scatter(X, y, s=10)
# 정렬된 X 값에 따른 y 값 예측
sorted_zip = sorted(zip(X, y_poly_pred))
X, y_poly_pred = zip(*sorted_zip)
plt.plot(X, y_poly_pred, color='m')
plt.title('polynomial regerssion')
plt.xlabel('area')
plt.ylabel('price')
plt.show()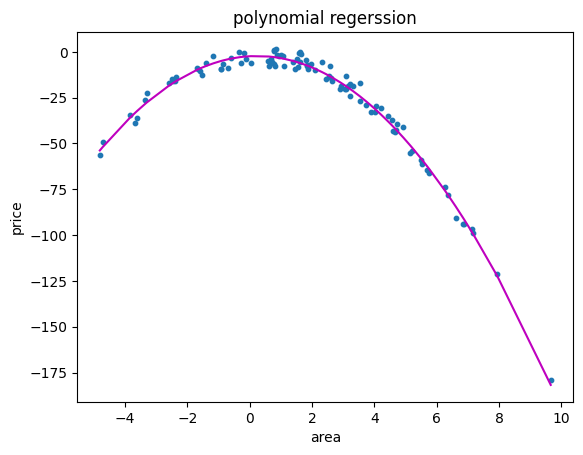
X_poly.shape
# 결과: (100, 3) -> 2차식으로 정의
1열: 절편항
2열: 1차항
3열: 2차항

