6. 자료구조

Elenaljh·2023년 6월 20일

CS50

목록 보기

9/14

6. 자료구조

1. malloc과 pointer 복습

1. 포인터변수와 쓰레기값(garbage value)

#include  <stdio.h>
#include  <stdlib.h>

int  main(void)
{
	int *x;
	int *y;

	x = malloc(sizeof(int)); // 주석1

	*x = 42;
	*y = 13;  // 주석2
}

주석
1. malloc: 할당된 메모리의 첫 바이트 주소를 되돌려줌, 메모리가 부족한 경우 NULL 반환.
2. 컴파일시 여기에서 문제 발생. error: variable 'y' is uninitialized when used here 포인터 y는 선언했으나, malloc을 이용해 메모리를 할당하지 않았기 때문에 쓰레기값(garbage value)이 저장된다. 이건 굉장히 위험한 상황인데, 그림으로 표현해보면 다음과 같다.

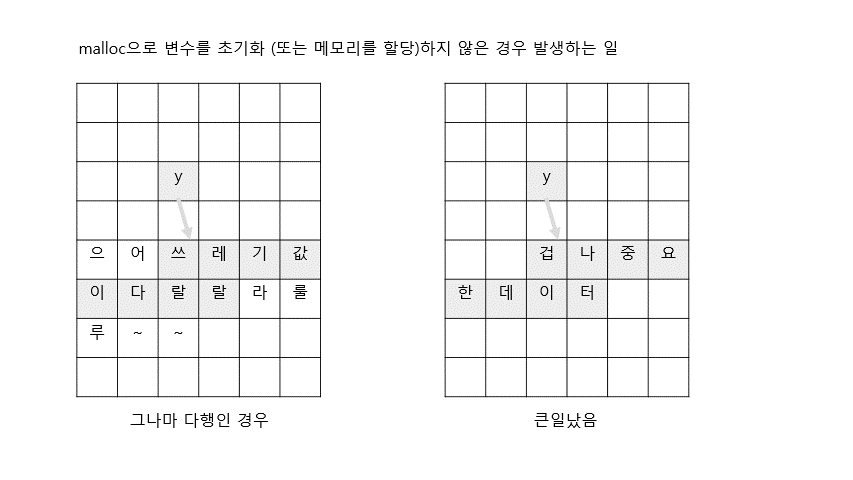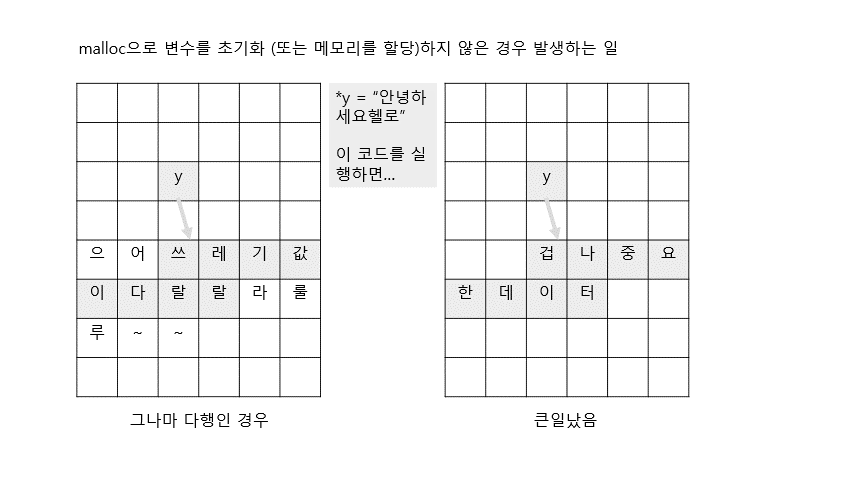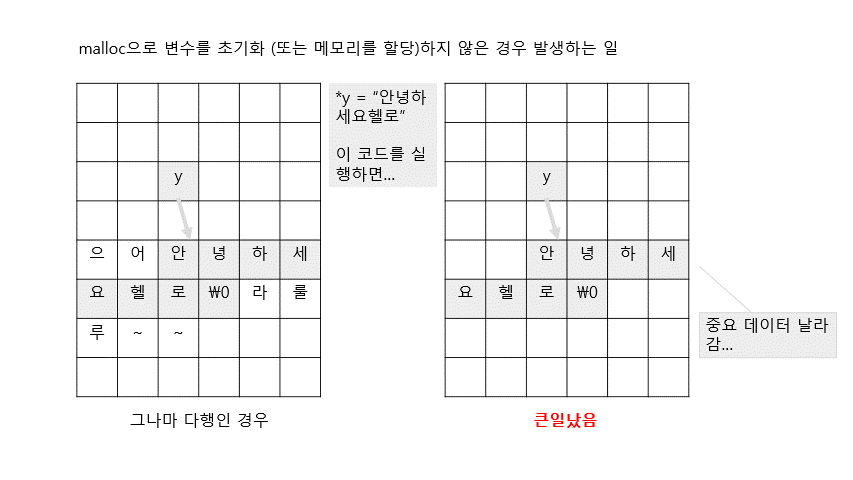
위의 코드를 옳게 바꾸면 다음과 같음.

#include  <stdio.h>
#include  <stdlib.h>

int  main(void)
{
	int *x;
	int *y;

	x = malloc(sizeof(int)); 

	*x = 42;
	y = x; //추가 
	*y = 13; 
}

이 경우 x와 y는 동일한 메모리 주소값을 가지게 됨. 따라서 x에는 42가 저장되었다가 13이 다시 저장되게 된다 (y때문에). 어쨌든 오류는 발생하지 않음.

2. 쓰레기값 방지하는 법

malloc을 이용해 따로 메모리를 할당하고 거기에 포인터 연결 ex. int *a = malloc(sizeof(int));
포인터변수 선언시 NULL을 이용해 값을 초기화하기 ex. int *a = NULL;

3. 참조와 역참조

참조(&)
포인터에 메모리 주소를 저장하는 것
역참조(*)
포인터에 저장된 주소로 가서 그 곳에 저장된 값에 접근하는 것.

4. 생각해보기

:bulb: 포인터를 초기화시키지 않고 값을 저장하면 어떤 오류가 발생할 수 있을까요?
포인터변수에 메모리 주소가 랜덤으로 저장되는데(쓰레기값), 운이 나쁘면 운영체제파일같은 중요한 정보가 저장된 메모리 주소가 포인터변수에 저장될 수 있다. 그 정보를 다른 정보로 덮어쓰기하는 경우 시스템에 중대한 오류가 발생할 수 있다.

2. 배열의 크기 조정하기

:pushpin: 핵심 단어: malloc, realloc

1. 배열의 크기 키우기

일정한 크기의 배열이 주어졌을 때, 그 크기를 키우려면 어떻게 해야할까?
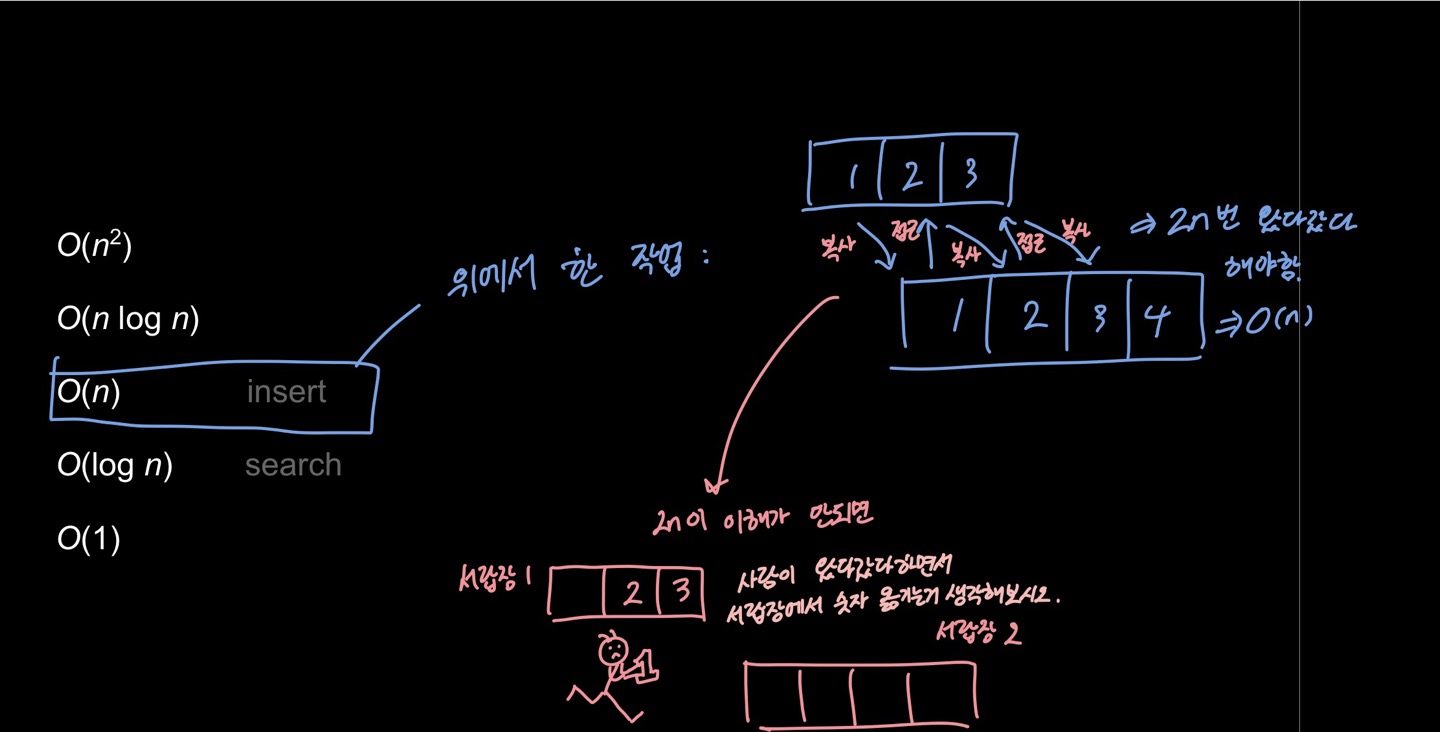
단순히 현재 배열이 저장되어있는 메모리 위치의 바로 옆에 일정 크기의 메모리를 더 덧붙이면 되는 것 같지만, 실제로는 그 옆에 다른 데이터들이 저장되어있을 확률이 높다. 따라서 안전하게 새로운 공간에 메모리를 다시 할당하고 기존 배열의 값들을 하나씩 옮겨줘야 한다.

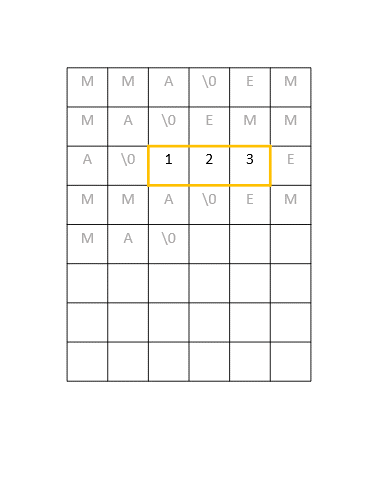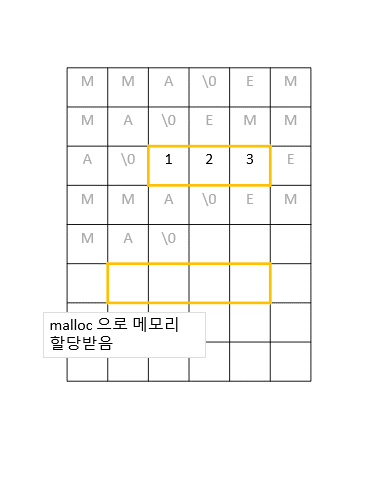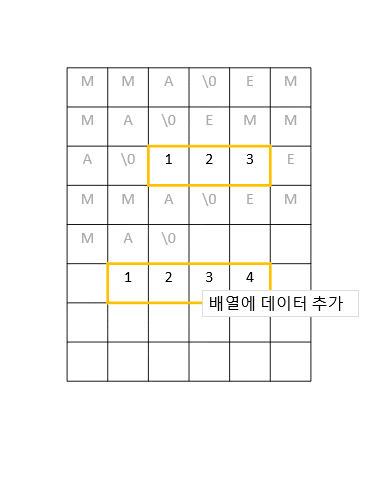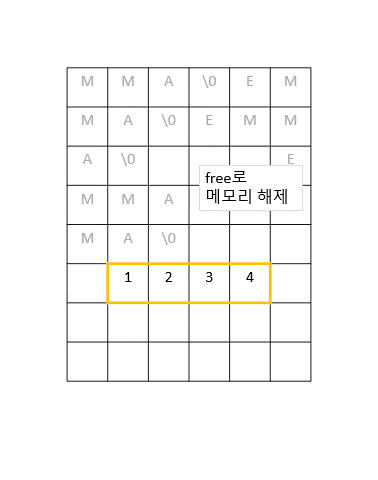
이 작업은 O(n), 즉 배열의 크기 n만큼의 실행 시간이 소요된다.

2. malloc을 이용해 배열의 크기 키우기

#include  <stdio.h>
#include  <stdlib.h>  //malloc, free 함수가 저장되어있음

int  main(void)
{
	//int 자료형 3개로 이루어진 list라는 포인터를 선언하고 메모리 할당
	int *list = malloc(3 * sizeof(int));

	//안전성 점검(malloc은 메모리가 부족하면 NULL을 반환한다)
	if (list == NULL)
	{
		return  1; // 만약 malloc이 NULL을 반환했다면(메모리가 부족) 프로그램을 종료한다
	}

	//list배열의 각 인덱스에 값 저장
	list[0] = 1; //각주 4 참고
	list[1] = 2;
	list[2] = 3;

	//int 자료형 4개 크기의 tmp라는 포인터를 선언하고 메모리 할당	
	int *tmp = malloc(4 * sizeof(int));  //주석 5 참고

	if (tmp == NULL)
	{
		return  1;
	}

	//list의 값 tmp로 복사
	for (int i = 0; i < 3; i++)
	{
		tmp[i] = list[i]; //할당된 새 메모리 덩어리(tmp)를 배열처럼 대괄호 써서 사용 가능
	}

	//tmp배열의 네 번째 값도 저장
	tmp[3] = 4;

	//기존 메모리(list) 해제
	free(list);

	//tmp 이름 계속 쓰는건 좀 바보같으니까 list로 이름 바꾸기
	list = tmp; 

	//새로운 배열 list의 값 확인
	for (int i = 0; i < 4; i++)
	{
		printf("%i\n", list[i]);
	}

	//프로그램이 끝나기 전 list의 메모리 초기화
	free(list); 
}

헤더 파일 안넣으면 나오는 에러: implicitly declaring library function 'malloc' with type 'void * 어쩌고 저쩌고..
malloc은 포인터를 반환하지만 메모리 덩어리를 할당하기 때문에 배열과 비슷하게 대괄호 기호[]를 사용할 수 있다. 그 이유는 배열도 메모리 덩어리이기 때문이다. 이렇게 보면 포인터 개념(malloc)과 배열이 동일한 것이라고 착각할 수 있다.
그러나 배열은 자동으로 free(기존 메모리 해제)가 되지만 malloc은 그렇지 않기 때문에 이런 차이점은 주의해야 한다.
malloc이나 realloc으로 메모리를 할당받을 때마다 널이 반환되었는지 확인해보는 습관을 들여야 한다.
포인터 이름 옆에 대괄호를 쓰면 (ex. a[i]) 컴퓨터는 자동으로 (포인터 주소 + i*sizeof(자료형)) 주소로 이동.
ex. int의 크기는 4바이트 -> 따라서 list[1] 주소 = list[0] 주소 + 4bytes
만약 임시변수(tmp)를 안만들고 바로 list = malloc~~ 이라는 코드를 넣으면 기존 정보는 포인터를 잃고 컴퓨터 메모리 안을 떠돌게 된다.. 물론 우린 이제 그 정보들을 찾을 수 없음ㅋㅋㅋ

솔직히 위의 코드는 너무 길다. tmp에 메모리 할당하고, list의 원소들을 tmp에 옮기고, 내용 추가하고, 마지막에 기존 메모리 free하는 과정을 하나로 합친 함수가 있다: realloc (re-allocate the chunk of memory)

3. realloc을 이용해 배열의 크기 키우기

#include  <stdio.h>
#include  <stdlib.h>

int  main(void)
{
	int *list = malloc(3 * sizeof(int));
	if (list == NULL)
	{
		return  1;
	}

	list[0] = 1;
	list[1] = 2;
	list[2] = 3;

	//tmp포인터에 메모리를 할당하고 list의 값 복사
	int *tmp = realloc(4 * sizeof(int)); //realloc 사용 - 각주 참고
	
	// 안전장치 - 메모리 있는지 검사
	if (tmp == NULL)
	{
		return  1;
	}

	//tmp 변수명을 list로 변경
	list = tmp;

	//새로운 list의 네 번째 값 저장
	list[3] = 4;
  
	//list의 값 확인
	for (int  i = 0; i < 4; i++)
	{
		printf("%i\n", list[i]);
	}
 
	//list의 메모리 초기화
	free(list);
}

realloc은...
1. 이미 할당받은 기존 메모리 덩어리를 새롭게 가져오고 원래보다 크든 작든 새롭게 설정된 크기로 바꾸는 일을 한다.
2. realloc은 기존 배열에서 새로운 배열로 데이터를 복사해주고, 기존 메모리는 자동으로 해제해줌-free(기존 배열)
3. 우리들은 뭔가 잘못되지는 않았는지(realloc이 NULL값을 반환하는지) 체크하고 잘못된 것이 없다면 새로운 배열에 새로운 값을 추가적으로 저장하면 됨

4. 생각해보기

:bulb: 이미 할당된 메모리의 크기를 조절할 때 임시 메모리를 새로 할당해줘야 하는 이유는 무엇인가요?
만약 임시변수(tmp)를 안만들고 바로 list = malloc~~ 이라는 코드를 넣으면 기존 정보는 포인터를 잃고 컴퓨터 메모리 안을 떠돌게 된다. 그럼 우린 이제 그 정보들을 찾을 수 없게 된다..

3. 연결 리스트: 도입

:pushpin: 핵심 단어: 연결 리스트
:pushpin: 복습: 구조체, 포인터

1. 데이터 구조란

데이터구조는 우리가 컴퓨터 메모리를 더 효율적으로 관리하기 위해 새로 정의하는 구조체(structure)이다. C에서 자료구조(데이터구조)는 아래 3가지 문법으로 이뤄진다.
|문법|설명|
|---|---|
|struct|구조체. 비트맵이나 비트맵 헤더 등과 관련된 문제에서도 구조체 사용|
|.|구조체의 속성값에 접근할 때 사용|
|*|역참조 연산자|

2. 연결 리스트 (Linked list)

1. 배열

배열은 1. 데이터 수정시 느리지만 2. 데이터에 접근할 때는 빠르다.
우선, 배열의 길이를 늘리거나 줄이기 위해서는 앞에서 배운대로 malloc이나 realloc을 이용해 메모리를 새로 할당받고, 기존 배열의 내용을 복사해서 새로운 배열에 붙여넣은 후 새 내용을 추가하거나 지우고, 마지막으로 기존 배열은 free를 통해 메모리를 해제시켜줘야 한다. 이 과정의 시간복잡도는 O(n) 으로 느리다.
그러나, 배열은 쉽게 인덱싱할 수 있어 값에 접근하는 것이 쉽고 빠르다. 또한 랜덤 접근이라는 방법으로 일정한 시간에 값에 접근할 수 있다(constant time access). 이런 면에서 배열은 매우 빠르다.

**constant time access란?**

"Every point in array is accessible in constant time."
우리는 배열에 포인터(메모리 주소)로 접근한다. 즉, 주소를 알기만 하면 별다른 과정을 거치지 않고도 바로 그 곳으로 갈 수 있는 것이다. 예를 들면
a[3] == *(location of a + n*sizeof(int))
인 것이다. 따라서 배열의 어느 위치에 접근해도 동일한 시간(constant time)이 소요된다.
이에 반해 연결 리스트(Linked list) 는 데이터의 수에 따라 값에 접근하는 시간이 달라진다 (accessible in "linear" time.). 연결 리스트에서 n번째 값에 접근하기 위해서는 n-1개의 원소를 거쳐야 하기 때문이다.

2. 연결 리스트

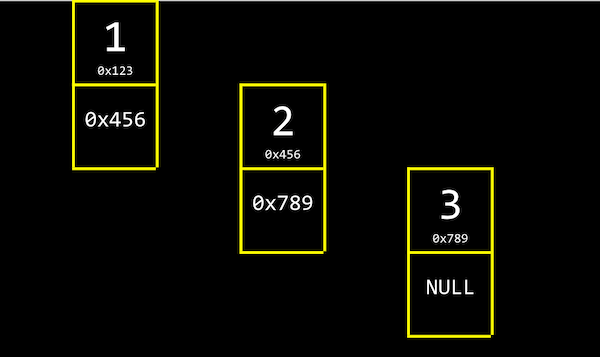연결 리스트의 형태는 위와 같다. 연결 리스트의 값들은 배열처럼 값이 서로 붙어있지 않다.(따라서 배열처럼 대괄호[]를 사용해 값에 접근할 수 없다.)

메모리의 빈 공간에 여기저기 값이 흩어져 있는 대신, 하나의 값에는 다음 값의 주소(포인터) 가 붙어있는 것이 연결 리스트의 특징이다. 포인터의 역할은 연결 리스트의 각 값을 연결하는 것이며, 리스트의 맨 마지막 값에는 NULL 포인터가 붙어있다.

**참고: NULL과 NUL**

종류	자료형	특징
NULL	pointer	값: 0x0
NUL	char	\0(널문자)

위 그림에서 값+포인터를 저장한 두 칸이 한 덩어리로 그려져 있는데, 이 덩어리를 node라고 한다.

3. 구조체로 연결 리스트 정의하기

구조체 복기

typedef struct
{
	string name;
	string number;
}
person;

person이라는 자료형을 만들었었음. 구조체의 멤버 변수(member variable)은 name과 number임.
각 멤버 변수에는 person.name, person.number과 같이 .을 사용해 접근한다.

연결 리스트는 아래 코드와 같이 간단한 구조체로 정의할 수 있다.

typedef struct node  //struct node: 구조체의 정식 명칭 (formal name of structure)
{
    int number;
    struct node *next; //next라는 포인터는 node structure을 가리키도록 정의됨
}
node; //구조체의 별명(alias). typedef가 하는 일은 프로그램의 다른 부분에서 사용하기 쉽도록 node를 node structure의 별칭으로 사용하도록 정의하는 것이다. (It gives you an alias from struct node to just 'node')

node라는 이름의 구조체는 number와 next 두 개의 필드가 함께 정의되어 있다.
number은 각 노드가 가지는 값, next는 다음 node를 가리키는 포인터가 된다.
여기에서 typedef struct 대신 typedef struct node라고 'node'를 함께 명시해주는 것은, 구조체 안에서 node를 사용하기 위해서이다.

참고

typedef struct x
{
	int number;
	struct x *next;
}
node;  //struct x의 별칭

이런 식으로 코드를 작성해도 위의 struct node를 정의한 것과 동일한 결과가 나온다.

4. 생각해보기

:bulb: 연결 리스트를 배열과 비교했을 때 장단점은 무엇이 있을까요?
데이터의 접근, 탐색이 중요하다면 배열을 쓰자.
데이터의 추가, 삭제가 중요하다면 연결리스트를 쓰자.

1. 배열 vs 연결리스트

	배열	연결 리스트
개념	정적(static)인 자료구조로, 연속된 메모리 주소를 할당받음. 스택에 메모리가 할당됨. 크기 수정이 불가하고, 배열 크기 이상의 데이터 저장 불가. 그러나 데이터가 순차적으로 저장되기 때문에 인덱스를 사용할 수 있어 임의 접근(random access) 가 가능해짐	크기를 정할 필요가 없어 동적(dynamic)인 자료구조임. 힙에 메모리가 할당됨. 메모리 상 흩어진 노드들의 묶음인데, 각 노드에는 데이터와 다음 데이터를 가리키는 포인터(메모리 주소)가 저장됨. 크기에 제한이 없어 데이터 추가, 삭제가 굉장히 자유롭다. 그러나 배열처럼 연속적인 메모리 주소를 할당받지 않기 때문에 임의접근이 불가능하고, 순차 접근(sequential access) 방식으로 데이터를 탐색함. 트리구조를 만들때 많이 사용됨.
읽기	O(1)	O(N)
검색	O(N)	O(N)
삽입	O(N)/ 앞:O(N), 뒤:O(1)	O(N)/앞:O(1) , 뒤:O(N)
삭제	O(N)/ 앞:O(N), 뒤:O(1)	O(N)/앞:O(1) , 뒤:O(N)

읽기: 배열은 인덱스(주소)만 찾아가면 되므로 딱 한 단계만 필요하고, 연결 리스트에서는 각 노드를 거치면서 주소를 찾아야 하므로 최악의 경우 N단계가 필요함.
검색: 검색은 어떤 데이터를 찾고 그 인덱스를 얻는 것이다. 배열과 리스트 모드 검색하고 있는 값을 찾을 때까지 모든 셀(노드)를 확인해야 한다.
삽입
- 배열
  - 맨 뒤가 아닌 자리에 삽입할 때는 자료를 오른쪽으로 옮겨야 하므로 N단계가 필요함.
  - 맨 끝에 자료를 삽입할 때는 단순히 삽입하면 되므로 1단계만 필요
- 연결리스트 (데이터 삽입 자체는 O(1))
  - 맨 앞이 아닌 자리에 삽입할 때는 원하는 자리에 갈때까지의 노드를 거쳐야 하기 때문에 N단계를 거침.
  - 맨 앞에 삽입할 때는 그냥 삽입하면 되므로 1단계만 필요.
삭제
- 배열
  - 맨 뒤를 삭제하는 것은 O(1)
  - 맨 뒤가 아닌 자료를 삭제할 때는 나머지 데이터를 모두 왼쪽으로 옮겨야 함. O(N)
- 연결리스트
  - 맨 앞을 삭제하는 것은 O(1)
  - 맨 앞이 아닌 자료를 삭제할 때는 그 노드까지 가려면 앞의 모든 노드를 거쳐야 함. O(N)

연결리스트는 노드 덕분에 데이터의 추가, 삭제로부터 자유롭지만 탐색이 느림
배열은 데이터가 연속적이므로 탐색이 빠르지만 데이터의 추가, 삭제로부터 자유롭지 못함. 따라서 결론은 다음과 같다.
데이터의 접근, 탐색이 중요하다면 배열을 쓰자.
데이터의 추가, 삭제가 중요하다면 연결리스트를 쓰자.

cf. 일반적인 알고리즘 문제를 풀 때는 배열이 더 빠르고 편하다.(문제에서 N의 크기가 주어지기 때문) 또한 배열의 크기를 초반에 MAX로 잡는다면 배열이 더 빠르고 편리함(연결리스트는 요소를 삽입, 삭제할 때마다 메모리의 할당, 해제가 일어나는데, 시스템 콜(System call)을 사용하는 경우 시간이 꽤 소요되기 때문)

2. 연결리스트의 종류

일반적인 연결리스트 (Linear/Singly linked list)
- 뒤로만 탐색 가능
- 각 노드에 데이터와 다음 노드의 주소 저장
이중 연결 리스트 (Doubly linked list)
- 전/후로 탐색 가능
- 각 노드에 데이터, 이전 노드의 주소, 다음 노드의 주소 저장
- 얻고자 하는 데이터의 위치가 tail에 가깝다면 tail에서부터 역방향으로 탐색 가능하기 때문에 탐색시간을 줄일 수 있다.
원형 연결 리스트 (Circular linked list)
- 마지막 노드가 null을 저장하는 대신 처음 노드의 주소를 저장
- head에서부터 순회를 진행하다보면 다시 head로 돌아오는 구조.
- 이중 연결 리스트 + 원형 연결 리스트 = 이중 원형 연결 리스트

4. 연결리스트: 코딩

1. 연결리스트 순차적으로 추가하기

다른 사람의 코드 참고

segfault 오류 나는 코드

#include  <stdio.h>
#include  <stdlib.h>

int  main(void)
{
	//node 구조체 정의
	typedef  struct  node
	{
		int  number;
		struct  node *next;
	}
	node;

	//리스트의 첫번째 노드 가리킬 포인터(list) 정의하기
	node *list = NULL;
  
	//리스트의 첫번째 노드 만들고 값 입력하기
	node *n = malloc(sizeof(node));
	if (n == NULL)
	{
		printf("메모리 부족");
		return  1;
	}
	n  -> number = 2; //(*n).number = 2;와 동일한 의미
	n  -> next = NULL;

	//list에 첫번째 노드 주소 입력
	list = n;
	printf("%i->",n->number);
	free(n);  //이것때문에 segfault 발생

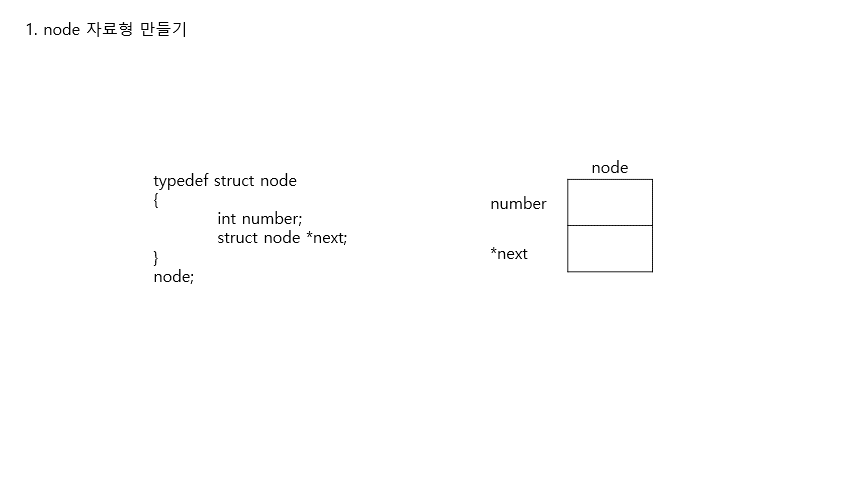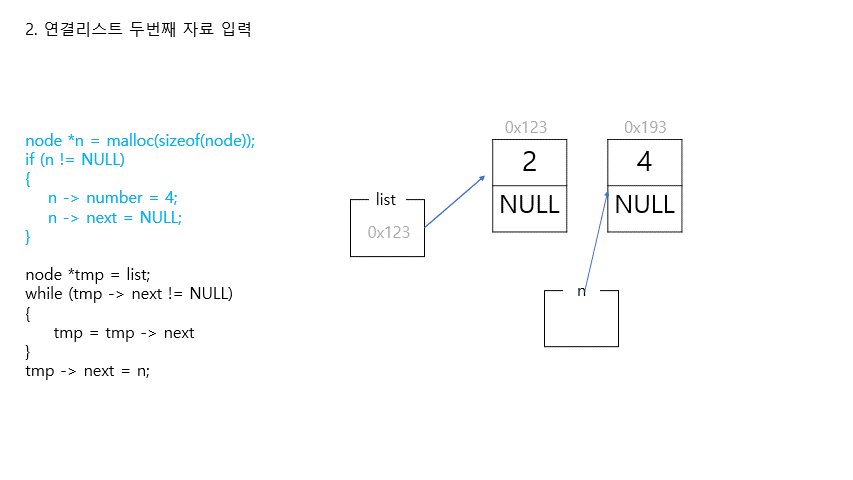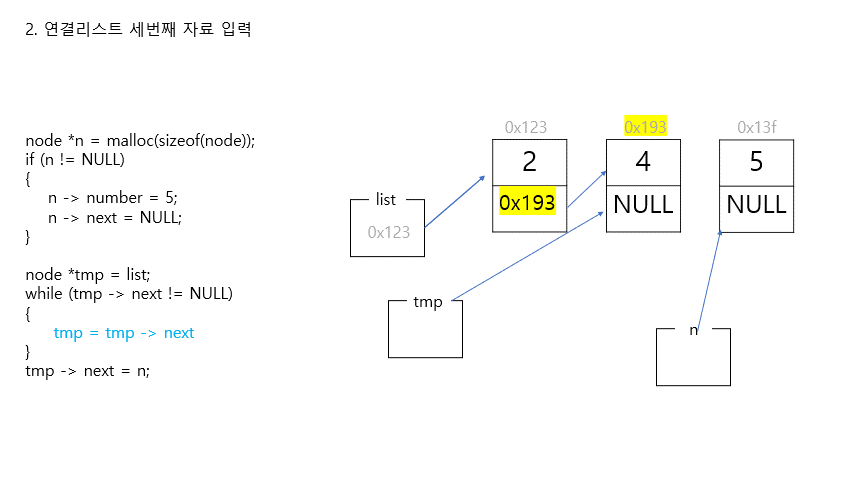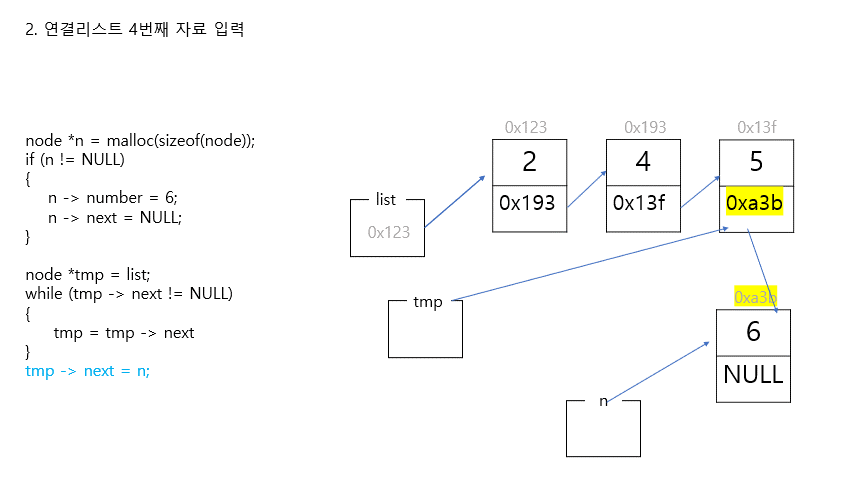
	//리스트의 두번째 노드 만들고 값 입력하기
	n = malloc(sizeof(node));
	if (n == NULL)
	{
		printf("메모리 부족");
		return  1;
	}
	n  -> number = 4;
	n  -> next = NULL;

	//첫번째 노드와 두번째 노드 연결하기
	//step1. 첫번째 노드에서 출발해서 추가한 노드의 직전 노드에 방문하기(순차적 접근)
	node *tmp = list;
	while (tmp->next != NULL)
	{
		tmp = tmp->next;
	}

	//step2. 직전 노드와 추가한 노드 이어주기
	tmp->next = n;
	printf("%i->",n->number);
	free(n);   //이것때문에 segfault 발생
}

망한 이유: malloc으로 할당한 메모리 n을 노드 하나 만들고 바로 free로 풀면 다음번에 malloc으로 메모리를 할당할 때, 전에 할당한 메모리를 다시 할당해버린다. 따라서 노드가 새로 만들어지는 것이 아니라 전에 만들었던 노드 위에 새로운 정보를 덮어쓰는 것이 되어버린다. 그래서 노드를 아무리 많이 만들어도 결과적으로 하나밖에 존재하지 않게 되고, 해당 노드의 next 필드는 NULL을 가리키게 된다. 그리고 3번째 노드(실제로는 존재하지 않지만 내가 생각하기에 3번째 노드)에 접근하려고 while문이나 for문을 돌렸을 때, n->next에 저장된 NULL값으로 가게 되어 segfault가 생긴다.
결론적으로 동적할당한 메모리를 해제하는 free는 프로그램이 끝나기 전에 넣거나 아예 해당 변수를 이후에 쓰지 않게 될 때 넣는 것이 좋다.

segmentation fault가 발생하는 이유

보호된 메모리에 접근할 때
읽기 권한이 없는 프로세스가 읽거나 쓰려고 할 때
할당된 메모리 이외 메모리에 접근할 때

잘 되는 코드

#include  <stdio.h>
#include  <stdlib.h>

int  main(void)
{
	//node 구조체 정의
	typedef  struct  node
	{
		int  number;
		struct  node *next;
	}
	node;
  
	//리스트의 첫번째 노드 가리킬 포인터(list) 정의하기
	node *list = NULL;
  
	//리스트의 첫번째 노드 만들고 값 입력하기
	node *n = (node*)malloc(sizeof(node));
	if (n == NULL)
	{
		printf("메모리 부족");
		return  1;
	}
	n  -> number = 2; //(*n).number = 2;와 동일한 의미
	n  -> next = NULL;

	//list에 첫번째 노드 주소 입력
	list = n;
	printf("%i->",n->number);

	//리스트의 두번째 노드 만들고 값 입력하기
	n = (node*)malloc(sizeof(node));
	if (n == NULL)
	{
		printf("메모리 부족");
		return  1;
	}
	n  -> number = 4;
	n  -> next = NULL;

	//첫번째 노드와 두번째 노드 연결하기
	//step1. 첫번째 노드에서 출발해서 추가한 노드의 직전 노드에 방문하기(순차적 접근)
	node *tmp = list;
	while (tmp->next != NULL)
	{
		tmp = tmp->next;
	}

	//step2. 직전 노드와 추가한 노드 이어주기
	tmp->next = n;
	printf("%i->",n->number);

2. 연결리스트 중간에 자료 삽입

//리스트 중간에 새로운 노드 삽입하기
//새로운 노드 만들기 (첫번째 노드와 두번째 노드 사이에 삽입할 것)

n = (node*)malloc(sizeof(node));
if (n == NULL)
{
	return  1;
}
n  -> number = 1;
n  -> next = NULL;

//포인터 연결하기
//step1. 새로운 노드와 그 다음 노드 연결하기
tmp = list;
for (int  i = 0; i < 1; i++)
{
	tmp = tmp->next;
}
n->next = tmp;
  
//step2. 새로운 노드와 그 전 노드 연결하기
tmp = list;
tmp->next = n;

//잘 연결됐나 확인
printf("\n");
for (tmp = list; tmp != NULL; tmp = tmp->next)
{
	printf("%i ->", tmp->number);
}
printf("NULL\n");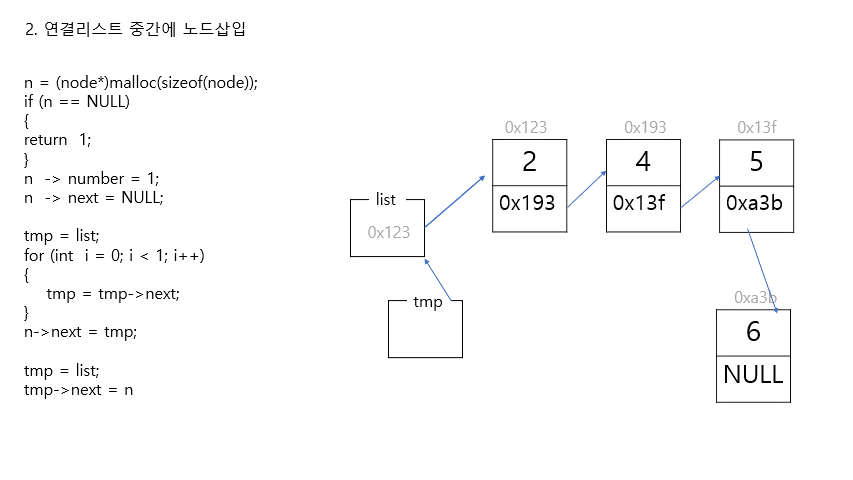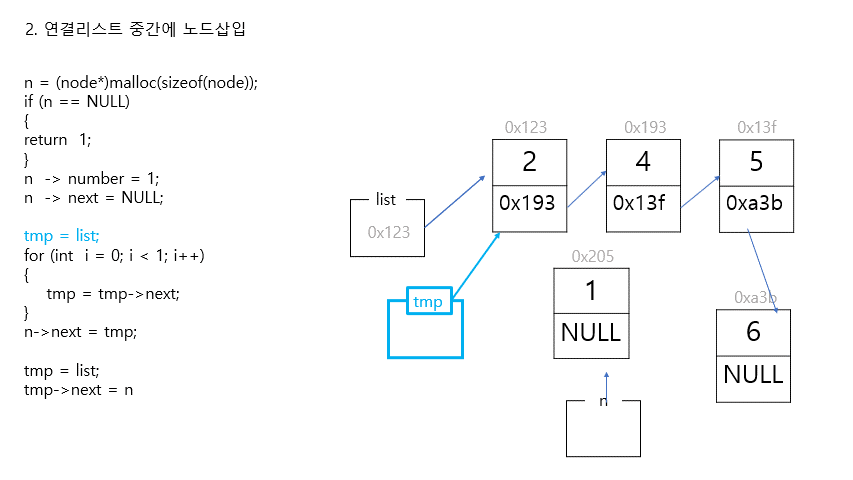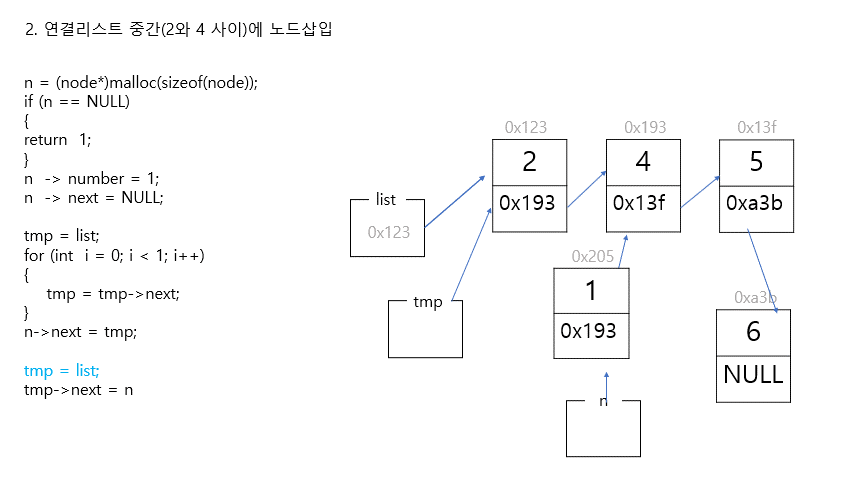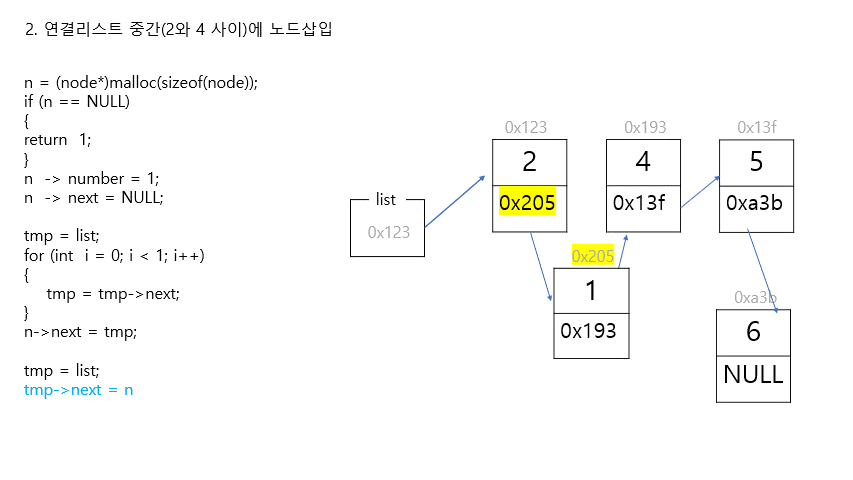

:pushpin:주의
노드를 중간에 삽입할 때는 무조건 뒷 노드를 연결한 후에 앞 노드와 연결해야 함. 다짜고짜 앞 노드부터 연결하면 앞 노드와 뒷 노드의 연결이 끊겨서 뒤쪽 리스트 전체가 날라간다. => 메모리 누수(Memory leak)

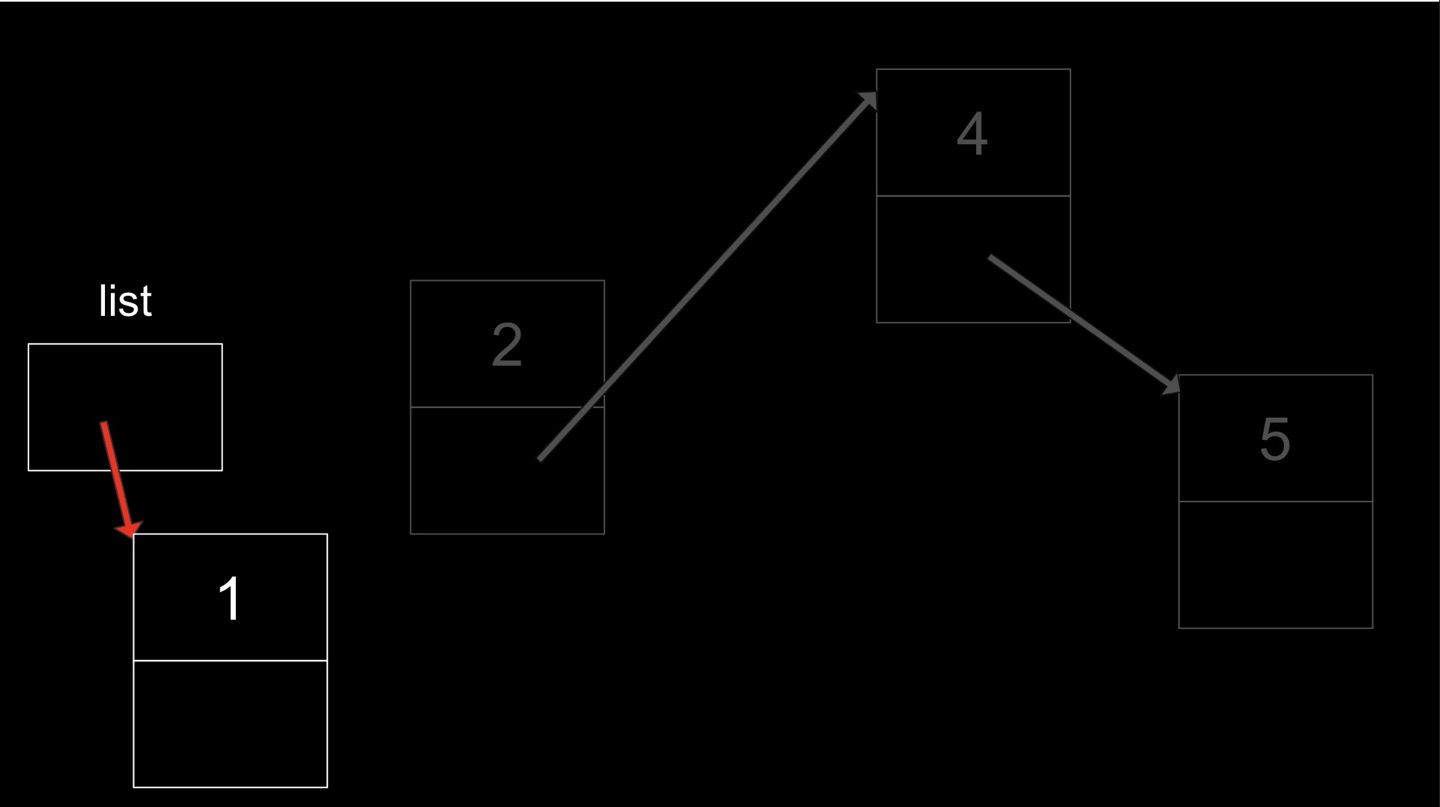
3. 연결리스트 중간에 추가했던 노드(두번째 노드) 삭제

//두번째 노드 삭제하기
node *pre = list;
node *remove = list;

// for (int i = 0; i < n-2; i++){pre = pre->next} => 지우고자 하는 (n번째)노드 바로 전의 노드를 pre가 가리키도록 함. 지금의 경우 n=2여서 이 과정 생략
remove = pre->next;
pre->next = remove->next; //n-1번째 노드와 n+1번째 노드 연결
free(remove); //n번째 노드 삭제

//잘 됐는지 확인해보기
printf("\n노드 삭제 결과: ");
for (tmp = list; tmp != NULL; tmp = tmp->next)
{
	printf("%i ->",tmp->number);
}
printf("NULL\n");

4. 생각해보기

:bulb: 연결 리스트의 중간에 node를 추가하거나 삭제하는 코드는 어떻게 작성할 수 있을까요?
3번에서 작성한 코드 참고

5. 연결 리스트: 시연

1. 연결 리스트의 장점과 단점

배열과 달리 연결리스트는 새로운 값을 추가할 때 다시 메모리를 할당하지 않아도 된다. 그러나 그 대가로 임의접근(Random access)이 불가하다. 따라서 이진탐색(binary search)도 할 수 없고, 순차적인 탐색(Sequential search)만 가능하다.
배열의 경우 정렬되어 있을 때 이진탐색이 가능하기 때문에 O(log n) 의 실행시간이 소요된다. 이에 반해 연결리스트는 찾는 것이 나올 때까지 각 위치를 순차적으로 탐색해야 하므로 O(n) 의 실행시간이 소요된다. 따라서 데이터를 탐색할 때 연결리스트는 다소 불리하다.
이처럼 여러 데이터 구조는 각각 장단점이 있으므로 경우에 따라 목적에 부합하는 가장 효율적인 데이터 구조를 고민해서 사용하는 것이 중요하다.

2. 연결 리스트의 node에 사용된 메모리 free하기

연결리스트를 만든 후 프로그램이 종료되기 전 malloc으로 할당받은 메모리를 모두 free해야 한다. 즉, 연결 리스트의 각 노드들을 모두 해제해야한다는 것이다. 코드는 다음과 같다.

//Free list: 연결리스트 만든다고 할당받은 메모리들을 다 free해야 한다. 
while (list != NULL)
{
	node *tmp = list->next;
	free(list);
	list = tmp;
}

이해 안가면 그려서 이해하셈. 얼마 안걸림.

3. 생각해보기

:bulb: 배열이 정렬되어 있지 않은 경우의 검색 소요 시간을 연결 리스트의 검색 시간과 비교해보세요.
배열이 정렬되어있지 않은 경우 검색시간: O(n)
연결리스트의 검색시간: O(n)
둘 다 비슷한 수준이다.

6. 연결 리스트: 트리

:pushpin:핵심 단어: 트리, 루트

1. 이진탐색트리 (Binary Search Tree)

아래 그림은 이진탐색트리(Binary Search Tree) 이다.

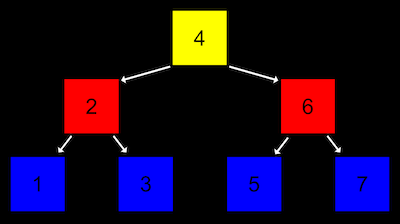
맨 위의 노란색 노드에서 트리가 시작되는데, 이 노드를 루트라고 한다. 루트 노드가 가리키는 하위 노드들을 자식 노드라고 한다.

이진 탐색 트리는 하나의 노드가 2개의 자식 노드를 가지는데, 1. 왼쪽 자식 노드는 자신의 값보다 작고, 2. 오른쪽 노드는 자신의 값보다 크다고 재귀적으로 정의할 수 있다.
따라서 이런 트리 구조는 이진 검색(Binary Search) 를 수행하는데 유리하여 검색하는데 소요되는 시간은 O(log n) 이다. 또한 포인터를 이용했기 때문에 연결리스트처럼 역동성도 가진다. 따라서 이진탐색트리는 탐색시간이 빠른 배열(이진탐색의 경우)의 장점과, 자료의 삽입/삭제가 쉬운 연결리스트의 장점을 모두 가진 자료구조라고 볼 수 있다.

2. 이진검색함수 코드

(실제로 돌아가는 코드는 아니다.. main()이 없기 때문에..)

#include <stdio.h>
#include <stdbool.h>   //boolean값 여기에 들어있음

//이진검색트리 노드구조체
typedef  struct  node
{
	int  number; //데이터
	struct  node *right; //오른쪽 자식 노드
	struct  node *left; //왼쪽 자식 노드
}
node;

//이진검색함수 (*tree는 이진검색트리를 가리키는 포인터) - 재귀함수 사용
bool  search(node *tree) //이 함수는 boolean을 반환한다.
{
	//Base case: 트리가 비어있는 경우 false 반환후 함수 종료
	if (tree == NULL)
	{
		return  false;
	}

	//현재 노드의 값이 50보다 크면 왼쪽 노드 검색
	else  if (50 < tree->number)
	{
		return  search(tree->left);
	}

	//현재 노드의 값이 50보다 작으면 오른쪽 노드 검색
	else  if (50 > tree->number)
	{
		return  search(tree->right);
	}

	//위 모든 조건 만족 X == 현재 노드의 값이 50
	else
	{
		return  true;
	}
}

cf. 이진 검색 트리를 활용했을 때 검색 실행 시간과 노드 삽입 시간은 모두 O(log n) 이다. 그 이유는 자료가 n개일 때
$\ 트리의 층 = log_2 n$ 이기 때문이다. 따라서 루트에서 가장 멀리 떨어진 자식노드에 찾고 있는 자료가 있는 최악의 경우에도 O(logn) 시간이 소요된다.

3. 생각해보기

:bulb: 값을 검색할 때 이진 검색 트리가 기본 연결 리스트에 비해 가지는 장점과 단점은 무엇이 있을까요?
장점: 정렬과 검색이 쉽고 빠르다 (검색 시간복잡도 - BST: O(log n), 연결: O(n))
단점: 연결리스트에 비해 코드가 복잡하다. 특히 자료를 삭제하거나 메모리를 free하는 과정이 복잡하다. 또한 메모리 공간을 더 많이 차지한다.

연결리스트 vs 이진검색트리

연결리스트는 이진트리의 일종이라고 한다(자식노드가 1개일 때의 트리)
||이진검색트리|연결리스트|
|---|---|---|
|포인터 수|0~2개|1개|
|검색|O(log n)-general/ O(n) - worst case|O(n)|
|삽입|O(log n) - general(balanced)/O(n) - worst case(unbalanced)|O(1)|
|삭제|O(log n) - general / O(n) - worst case|O(1)|
|정렬|정렬됨(노드의 왼쪽 트리는 항상 값이 작고 오른쪽 트리는 항상 값이 큼)|정렬X|
|장점|정렬과 검색이 쉽고 빠르다. 자료간 위계를 표현한다.|적용하기 쉽고 여러 적용사례도 많다.|
|단점|코드가 복잡하다. 특히 자료를 삭제하는 것이나 memory freeing이 복잡하다.|random access를 필요로 하는 유용한 정렬 알고리즘을 사용할 수 없다. |

7. 해시 테이블

:pushpin: 핵심 단어: 해시 테이블, 해시 함수

1. 인트로

연결리스트나 트리에서는 값을 검색할 때 O(n)또는 O(log n)의 시간이 걸린다. 해시테이블은 이 시간을 더 단축해 검색시간을 거의 O(1)에 가깝게 만들어준다.

2. 해시테이블

해시 테이블은 '연결 리스트의 배열' 이다. 즉, 배열의 장점인 random access와 연결리스트의 장점인 dynamism(정해진 크기가 없음)을 모둔 취한 자료구조인 것이다.
여러 값들을 몇 개의 바구니에 나눠 담는 상황을 생각해보자. 각 값들은 '해시 함수'라는 맞춤형 함수를 통해 어떤 바구니에 담기는지 결정된다. 각 바구니에 담기는 값들은 그 바구니에서 새롭게 정의되는 연결 리스트로 이어진다. 이렇게 연결 리스트가 담긴 바구니가 여러 개 있는 것이 '연결 리스트의 배열', 즉 해시테이블이 된다.

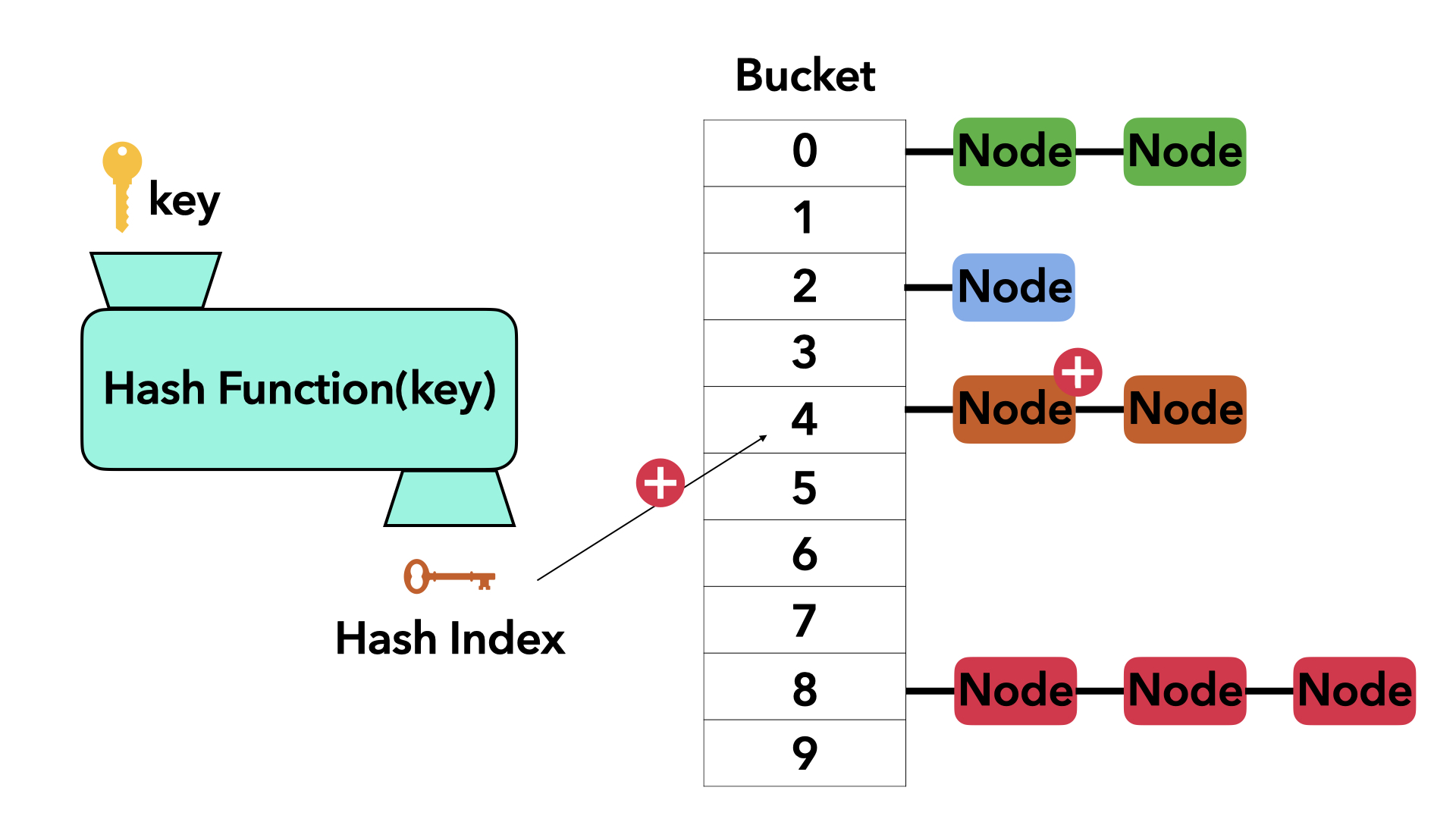
해시테이블을 사용하는 방법은 간단하다. key를 해시 함수에 넣으면, 해시인덱스(또는 해시코드-non integer value-)가 나오고, 해당 인덱스를 통해 빠르게 데이터를 찾아 들어간다.

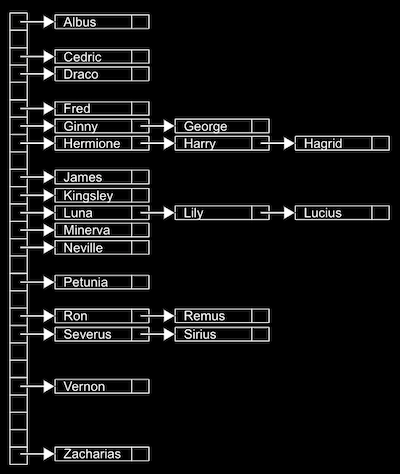위 그림을 보면 세로로 길게 연결된 칸들이 이름이 담길 바구니이다. 각 바구니는 이름의 가장 첫 글자에 따라 분류되는데, 이 때 **이름의 첫 글자가 해시 함수**이다. 이 해시테이블에는 알파벳 개수에 해당하는 총 26개의 **포인터**들이 있고, 각 포인터는 그 알파벳을 시작으로 하는 이름들을 저장하는 **연결리스트를 가리킨다.** H가 담긴 바구니에는 Hermione, Harry, Hagrid로 구성된 연결리스트가 들어있어 다른 연결리스트보다 길다. Vernon은 리스트의 원소가 하나기 때문에 한번에 찾을 수 있지만(각 바구니는 배열을 구성하므로 V 바구니는 O(1), 즉 바로 찾을 수 있다.) Hagrid를 찾으려면 앞의 Hermione, Harry도 검사해야 하므로 3번의 검사과정이 추가적으로 필요하다. 따라서 모든 사람들의 이름이 H로 시작하는 최악의 경우를 생각해본다면 해시테이블의 검색시간은 **O(n)** 으로 늘어날 수 있다.

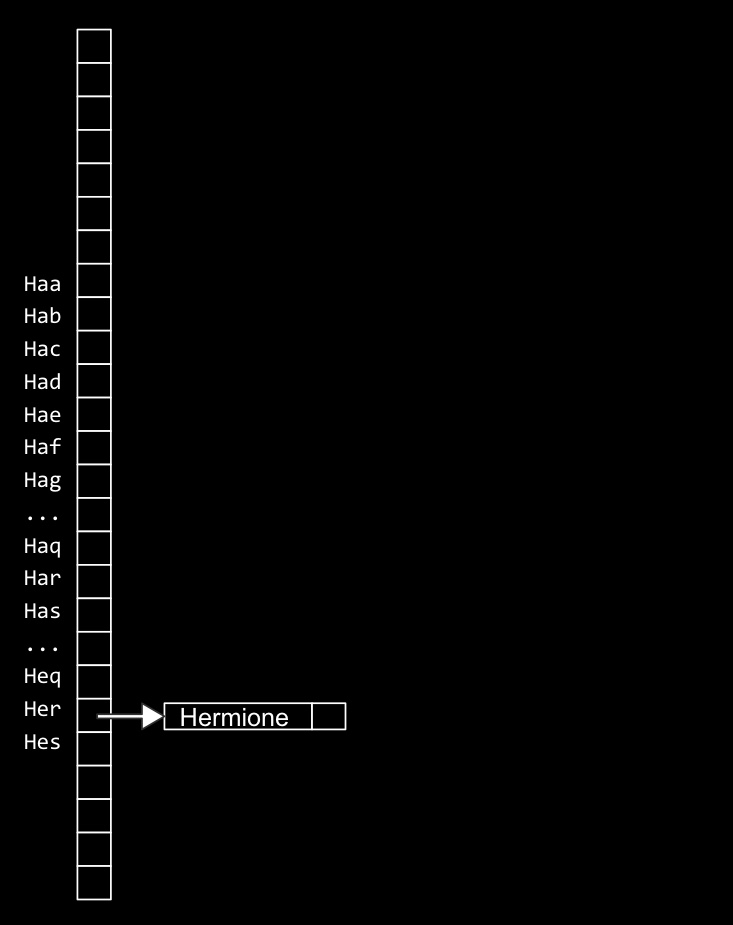
위의 그림을 보자. 처음과 다르게 이름 분류 기준(또는 해시함수)을 최대한 세세하게 나눈 것이다(이름 첫 두 글자 + a,b,c,d,e..) 이 경우 배열이 차지하는 공간이 많아져서 공간복잡도가 늘어나지만, 한 바구니 안에 이름이 많이 들어가지는 않으므로(충돌-collision-이 없다/ 연결리스트가 매우 짧아진다) 이름이 한 개만 들어간 최선의 경우 검색시간은 O(1) 까지 줄어들 수 있다.
일반적으로는 최대한 많은 바구니를 만드는 해시 함수를 사용하기 때문에 해시테이블의 시간복잡도는 거의 O(1)에 가깝다고 볼 수 있다. (해시 테이블은 데이터가 입력되지 않은 여유공간-바구니-가 많아야 제 성능을 유지할 수 있다. 공간 사용률이 70~80%부터 성능 저하가 일어난다.)

3. 좋은 해시함수의 조건

Use only the data being hashed
Use all of the data being hashed
Be deterministic: input값이 같으면 return값도 항상 같아야 함.
Uniformly distribute data: 데이터가 여러 바구니에 골고루 나뉘어 있어야 한다. 즉, 하나의 이름바구니에 모든 이름을 집어넣거나, 특정 바구니에만 쏠리게 넣으면 안된다는 뜻.

3. 충돌(Collision)

가장 이상적인 해시테이블은 한 버켓(바구니)에 딱 한개의 노드(위의 예시에서는 이름)가 있는 경우이다. 하지만 현실은 그렇게 하기가 힘든데, 한 버켓에 여러개의 노드(이름)가 있는 경우를 충돌이라고 한다.
충돌을 해결하는데에는 크게 2가지 방법이 있다.

체이닝(Chaining): 각 해시코드에 연결리스트를 저장하는 방법. 그럼 위의 이미지와 같은 자료구조가 탄생한다.
- 개방주소방법의 문제점(clustering, infinite loop 해결)
- 해시테이블에 null 상태의 포인터들을 저장. 각 포인터들은 그에 맞는 연결리스트의 주소를 저장한다.
- 만드는 방법
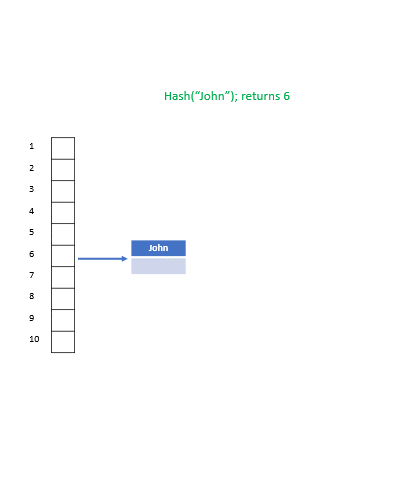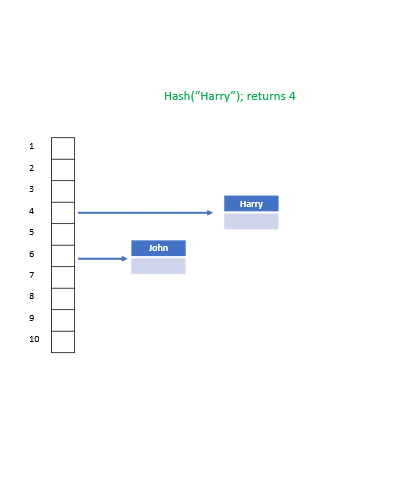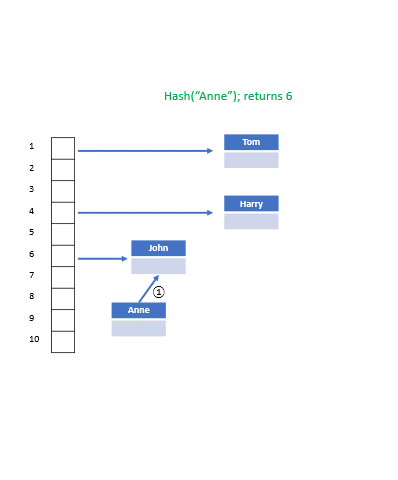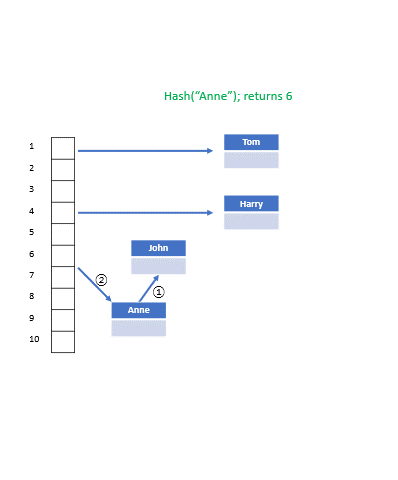
개방주소방법-선형조사 (Linear probing): 인덱스에 이미 다른 노드가 있다면 바로 앞뒤의 인덱스(hashcode+1,2,..n)를 탐색해서 빈 인덱스에 삽입하는 방법 $$ h_i(x) = (h(x) + i) mod m $$

- 장점1. 체이닝처럼 포인터가 필요없고, 지정한 메모리 외 추가적인 저장공간도 필요 없다. 삽입, 삭제시 오버헤드가 적고 저장할 데이터가 적을 때 유리하다.
- 문제1. Clustering - 예를 들어 John, Mary, Ethan, Harry,.. 등 여러 이름을 입력한 결과 hashcode가 모두 7이 나왔다고 하자. 그럼 개방주소법에 따라 hashcode 6,8에 저장하고, 5,9에 저장하고.. 이런 과정을 반복하게 된다. 그 결과 데이터가 한 군데에 몰려있게 된다. 이 현상을 clustering이라고 한다.
- 문제2. Infinite loop: 입력 데이터는 100개인데 해시코드는 10개일 경우, 10개의 데이터를 다 입력하면 빈 해시코드는 없게 된다. 그럼 11번째 데이터를 입력하는 과정에서 빈 해시코드를 찾는 코드가 무한루프에 빠지게 된다.
개방주소방법 - 이차원조사
$\ h_i(x) = (h(x) + i^2) mod m $$$ \ h_i(x) = (h(x) + c_1i^2 + c_2i)modm$$
개방주소방법 - 더블 해싱
$\ h_i(x) = (h(x) + if(x)) mod m$
여기서 h(x)와 f(x)는 서로 다른 해시함수다. f(x)의 값은 해시테이블 크기 m과 서로소여야 한다. 권장: h(x) = x mod m, f(x) = 1+(x mod m)

4. 정리

출처
참고: 해시키 계산 - O(1), 인덱스찾기 - O(1)

1. 시간복잡도 (open addressing)

-> linear probing
|작업|best case|average case|worst case|
|---|---|---|---|
|삽입|O(1)|O(1)|O(n)|
|ㄴ|해시키가 빈 인덱스를 가리켜서 그 자리에 바로 자료 삽입|||
|삭제|O(1)|O(1)|O(n)|
|ㄴ|계산한 키로 접근한 인덱스에 자료가 있어서 바로 지움|||
|검색|O(1)|O(1)|O(n)|
|ㄴ|해시키 계산하고 바로 데이터 찾음||해시맵이 모두 찬 경우, 해시키를 통해 해시맵의 인덱스에 접근했어도 그 자리에 찾는 자료가 없을 수 있음. 이 때 해시맵을 전부 돌아다니면서 자료를 찾아야 함 = O(n) (n=데이터 개수)|
|공간복잡도|O(n)|O(n)|O(n)|

2. 시간복잡도 (chaining)

O(1) = O(c) = constant time complexity
|작업|best case|average case|worst case|
|---|---|---|---|
|삽입|O(1)|O(1)|O(n)|
|ㄴ||모든 연결리스트가 동일한 길이 - 따라서 리스트의 마지막 노드에 도달하는 것 = O(1), 그 뒤에 새로운 노드를 추가하면 됨: O(1)|모든 자료가 단 하나의 인덱스의 연결리스트에 저장됨. 그 리스트의 마지막 노드에 가는 것은 O(n). 그 후 삽입 - O(1)|
|삭제|O(1)|O(1)|O(n)|
|ㄴ||삭제할 노드에 도달:O(1), 삭제하는 것 자체는 O(1)|모든 자료가 단 하나의 인덱스의 연결리스트에 저장됨. 그 리스트의 마지막 노드에 가는 것은 O(n). 그 후 삽입 - O(1)|
|검색|O(1)|O(1)|O(n)|
|ㄴ||연결리스트에서 자료 찾기-O(n/m)=O(c)=O(1) (각 연결리스트의 길이가 같다고 가정. 즉, 모든 연결리스트의 n값은 동일)||
|공간복잡도|O(m+n)|O(m+n)|O(m+n)|
m= size of the hash table
n= number of items inserted

2. 단점

데이터를 정렬(ordering and sorting)하는데 시간이 많이 걸린다.
- 해시테이블에서 데이터를 정렬하려고 시도하면, 해시테이블 고유의 장점은 잃고 정렬시간이 n에 가까워진다.
- 따라서 데이터 정렬여부가 중요하지 않은 경우에 해시테이블을 사용한다.
모든 key type에 대해 강력한 해시함수를 요구하기 때문에 다른 자료구조에 비해 (좋은 해시함수를)설계/구현/디버그가 쉽지 않다.

5. 생각해보기

:bulb: 해시 함수는 어떻게 만들 수 있을까?
cf. 조교의 조언: 해시함수는 그냥 인터넷에서 찾아서 써라. 자기만의 해시함수를 만드는건 시간낭비다ㅋㅋ 대신 출처는 표기하셈.
해시함수를 만드는 방법은 대표적으로 두 가지 방법이 있다.
더 많은 방법이 있긴 한데 여기 참고.

이것도 보던가

1.자릿수 선택(digit selection)

: 키값 중, 일부 자릿수 골라내어 인덱스 생성

: h(121234345656) ⇒ 113355 *key값 (예.주민번호) 중 홀수자릿수 선택

2.자릿수 접기(digit folding)

: 키값 각각의 자릿수를 더해 인덱스 생성

: h(123456) = 1+2+3+4+5+6 = 21

3.모듈로 연산(modulo function) - 많이 사용됨.

: 키를 해쉬테이블의 크기로 나눈 나머지를 인덱스로 생성

: h(157) ⇒ mod(157) = 7 *h(KEY) = KEY MOD TABLESIZE

나누기 방법
원소(정수일 경우 그냥 사용, 문자(열)의 경우 아스키코드 사용)를 해시 테이블의 크기로 나누어 나머지의 값을 테이블 주소로 사용해 저장하는 방식. 이 방법은 해시테이블 크기보다 큰 수를 해시 테이블 크기 범위에 들어오도록 수축시킨다.
$ $\ h(x) = xmodm $$
곱하기 방법
입력값을 0과 1 사이의 소수에 대응시킨 후, 해시 테이블 크기 m을 곱해 해시값을 0<h(x)<m에 대응시킨다. 이 방법을 쓰려면 해시함수의 특성을 결정짓는 상수 A(0<A<1)를 미리 준비해야 한다.
$ $\ h(x) = [m(xA mod 1)] $$
(xA mod 1 = xA의 소수부분)

8. 트라이 (Trie)

1. 트라이란?

트라이는 검색(retrieval)의 줄임말로, 기본적으로 트리 형태의 자료구조다. 트리와 구분되는 점은 각 노드가 배열로 이루어져있다는 것이다. Hermione, Harry, Hagrid를 저장해보겠다.

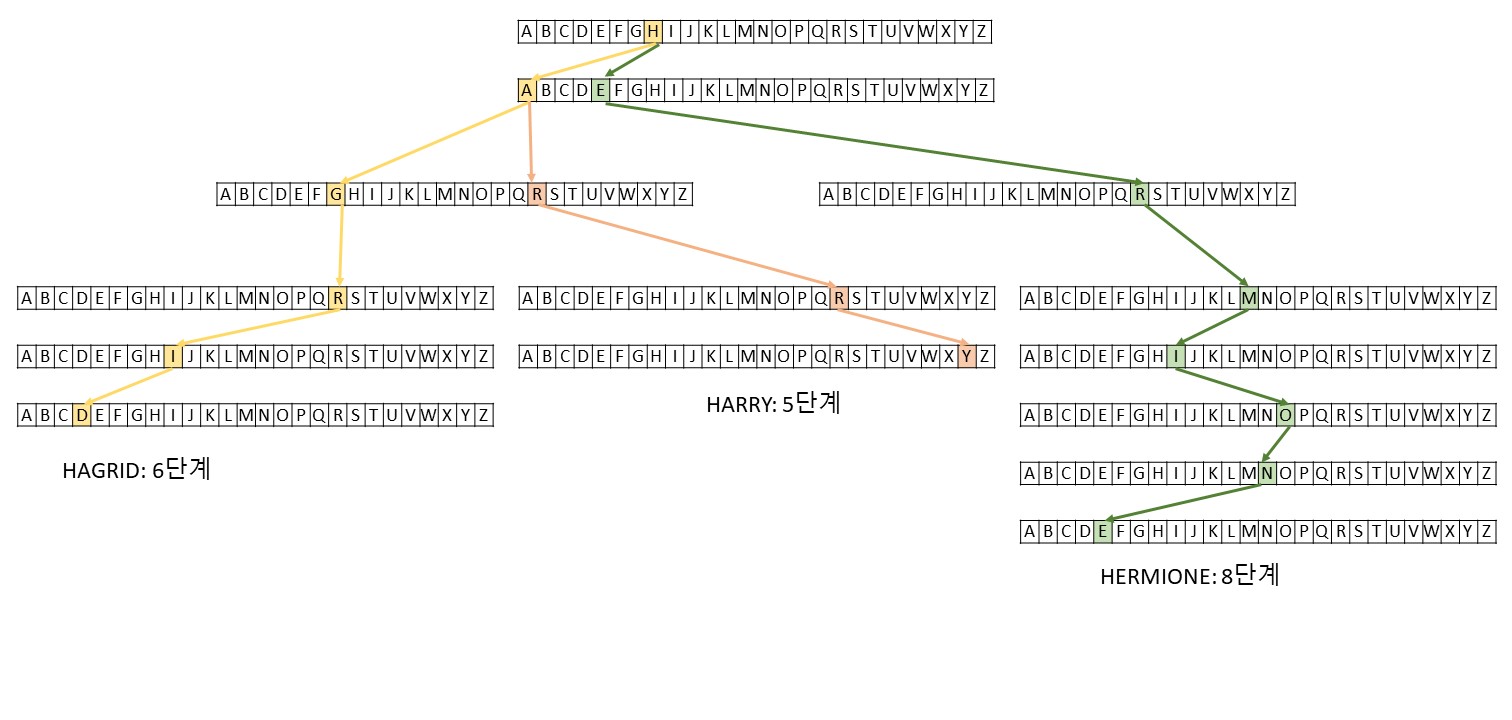
위와 같은 트라이에서 값을 검색하는데 걸리는 시간은 문자열의 길이에 한정된다. 다른 자료구조는 저장된 데이터의 양에 비례해 탐색시간이 늘어나지만, 트라이에서 자료를 탐색하는데 걸리는 시간은 데이터의 양과 관계없다. 대신 저장되는 자료의 길이에 따라 결정된다. 만약 트라이에 영어 이름을 저장한다면, 영어 이름의 길이가 k라고 할 때 O(k)≈O(1) 의 탐색시간이 걸리는 것이다.
트라이를 활용하는 대표적인 예는 텍스트 자동완성이다. bat를 치면 컴퓨터는 트라이의 루트를 타고 검색해서 batman, batch, battlenet 등을 추천해준다.

2. 트라이의 장점과 한계

트라이는 다른 자료구조에 비해 자료를 삽입, 삭제, 검색하는 시간이 매우 빠르다. -> 모두 O(1)
그러나 트라이는 각 노드가 배열로 구성된 매우 커다란 자료구조이므로, 저장되는 자료의 양에 비해 메모리를 많이 차지한다. -> 공간복잡도 O(포인터 자체 크기 한 노드에 포함된 포인터배열 길이 트라이에 존재하는 총 노드의 개수)

3. 해시테이블 vs 트라이

해시테이블: 키(해시코드)와 값(value)이 1:多의 관계가 될 수 있다(이를 충돌이라고 함) -> 이런 점을 트라이가 보완할 수 있음
트라이: 키가 unique하다. 즉, 해시테이블과 다르게 키와 값이 1:1관계이므로 충돌이 일어나지 않는다. 또한 그 어떤 데이터도 두 데이터가 동일하지 않은 이상 트라이 내부에서 로드맵이 동일하지 않다.

4. 트라이 만들기

1. 트라이 구조체 만들기 (키: 설립년도, 값: 대학 이름)

typedef struct _trie
{
	char university[20];
	struct _trie* paths[10];
}
trie;

2. 트라이에 자료 저장하기

1636년에 설립된 하버드를 저장해보자 (키:1636, 값:Havard)

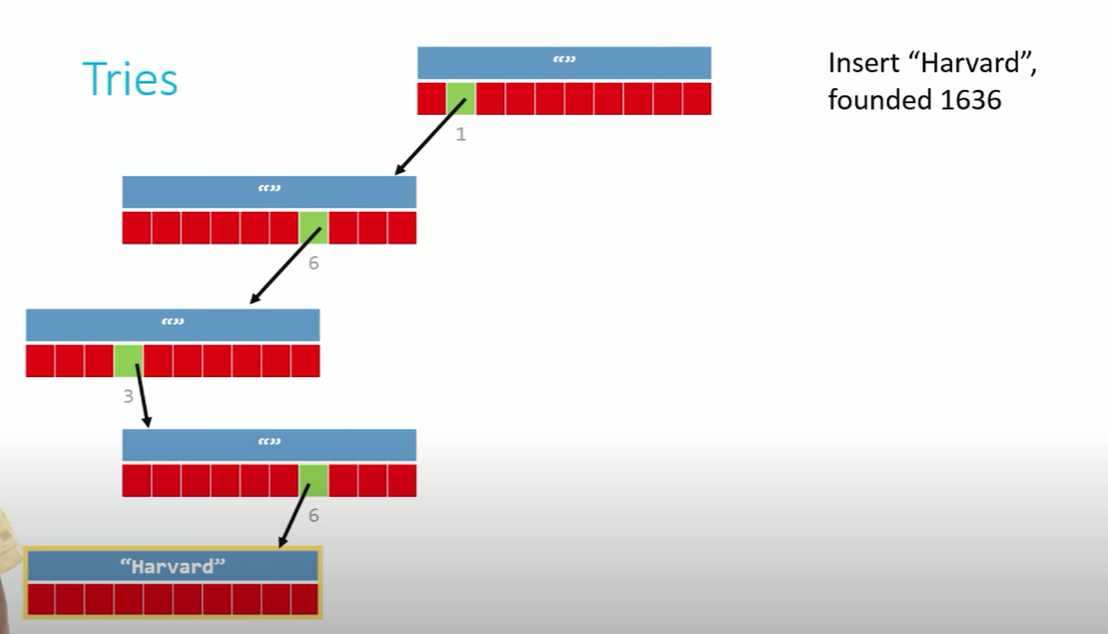
각 노드를 만들고 포인터로 연결하는 방법은 연결리스트를 만드는 방법과 동일하다. (malloc으로 노드 만들고 포인터로 연결)

1701년에 설립된 예일을 저장해보자 (키: 1701, 값: Yale)

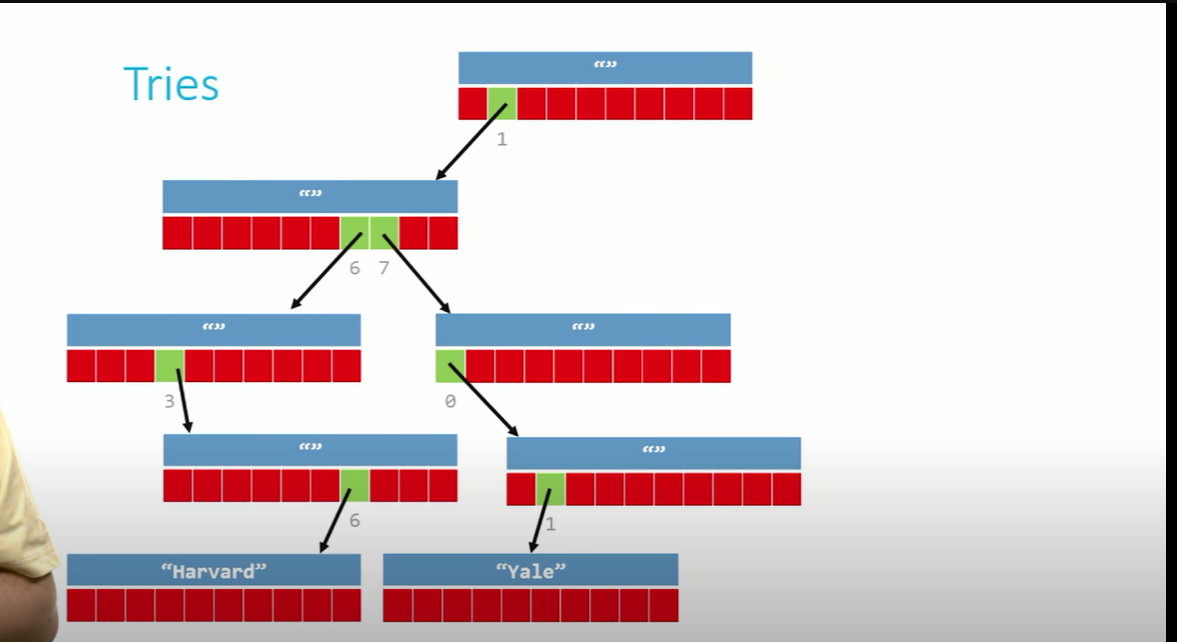
3. 트라이에서 검색하기

루트에서 시작해서 주어진 키를 따라갔을 때 null 포인터가 나오면 실패, 자료를 찾으면 성공.
주의할 점: bat를 찾는데 트리에 저장된 자료는 batch일 수 있음. 근데 batch안에 bat가 있으므로 bat를 찾았다고 착각할 수도 있음. 따라서 꼭 루트의 끝까지 따라간 후에 자기가 진짜 찾는 것이 있는지 확인해야 함.

5. 생각해보기

:bulb: 트라이와 해시테이블 비교
출처
||트라이|해시테이블|
|---|---|---|
|검색 속도|O(1)-특히 같은 자료들의 루트가 겹치거나 같은 요청이 반복적으로 들어와서 CPU cache되어 더 빨라짐.|충돌이 없는 경우 O(1)이지만, 충돌이 있을 때 최악의 경우 시간이 O(n)으로 늘어남|
|충돌(Collision)|없음=> key:value = 1:1|있음=> key:value = 1:多|
|공간복잡도|O(포인터 자체 크기 한 노드에 포함된 포인터배열 길이 트라이에 존재하는 총 노드의 개수)|open addressing: O(n), chaining: O(m+n)|
m: 연결리스트 길이
n: 자료 개수

9. Abstract data structures

1. 큐 (Queues)

선입선출 (FIFO)
배열, 연결리스트를 통해 구현 가능함

2. 스택 (Stacks)

후입선출 (LIFO)
배열, 연결리스트로 구현
ex) 이메일, 식당 트레이

3. 딕셔너리 (Dictionaries)

키 - 값으로 이루어짐
해시테이블과 동일한 개념 (hashkey - value)
키를 어떻게 정의할 것인지가 중요함.

4. 생각해보기

:bulb: 여태까지 배운 개념들을 기반으로 해서 나만의 새로운 자료 구조를 만들어 볼 수 있을까요?

Elenaljh

이전 포스트

5. 메모리

다음 포스트

6. 자료구조

CS50

6. 자료구조

1. malloc과 pointer 복습

1. 포인터변수와 쓰레기값(garbage value)

2. 쓰레기값 방지하는 법

3. 참조와 역참조

4. 생각해보기

2. 배열의 크기 조정하기

1. 배열의 크기 키우기

2. malloc을 이용해 배열의 크기 키우기

3. realloc을 이용해 배열의 크기 키우기

4. 생각해보기

3. 연결 리스트: 도입

1. 데이터 구조란

2. 연결 리스트 (Linked list)

1. 배열

2. 연결 리스트

3. 구조체로 연결 리스트 정의하기

4. 생각해보기

1. 배열 vs 연결리스트

2. 연결리스트의 종류

4. 연결리스트: 코딩

1. 연결리스트 순차적으로 추가하기

2. 연결리스트 중간에 자료 삽입

3. 연결리스트 중간에 추가했던 노드(두번째 노드) 삭제

4. 생각해보기

5. 연결 리스트: 시연

1. 연결 리스트의 장점과 단점

2. 연결 리스트의 node에 사용된 메모리 free하기

3. 생각해보기

6. 연결 리스트: 트리

1. 이진탐색트리 (Binary Search Tree)

2. 이진검색함수 코드

3. 생각해보기

7. 해시 테이블

1. 인트로

2. 해시테이블

3. 좋은 해시함수의 조건

3. 충돌(Collision)

4. 정리

1. 시간복잡도 (open addressing)

2. 시간복잡도 (chaining)

2. 단점

5. 생각해보기

8. 트라이 (Trie)

1. 트라이란?

2. 트라이의 장점과 한계

3. 해시테이블 vs 트라이

4. 트라이 만들기

1. 트라이 구조체 만들기 (키: 설립년도, 값: 대학 이름)

2. 트라이에 자료 저장하기

3. 트라이에서 검색하기

5. 생각해보기

9. Abstract data structures

1. 큐 (Queues)

2. 스택 (Stacks)

3. 딕셔너리 (Dictionaries)

4. 생각해보기

5. 메모리

7. Python

0개의 댓글