AutoEncoder

데이터사이언스 과목 기말 발표 주제를 오토인코더로 정했다.

** '핸즈온 머신러닝' 서적을 참고하여 작성했습니다.

개념

오토인코더란 ?

: 입력 데이터를 압축시켜 압축시킨 데이터로 축소한 후 다시 확장하여 결과 데이터를 입력 데이터와 동일하도록 만드는 일종의 Deep Neural Network 모델

Auto Encoder는 입력 데이터를 일종의 Label(정답)로 삼아 학습하므로 Self-supervised Learning 이라고 부르기도 하지만 어쨋거나 y값이 존재하지 않으며 이용하지 않는다는 점에서 Unsupervised Learning으로 분류되는 모델이다.

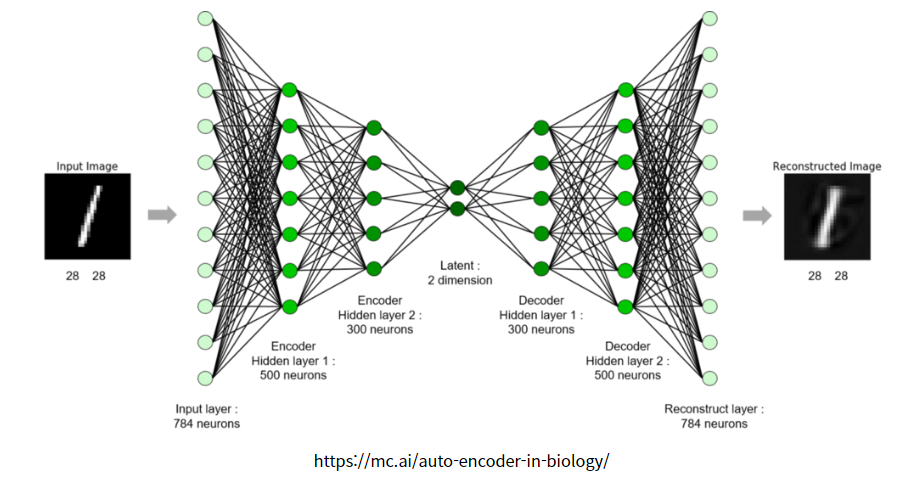
위 그림은 손글씨 이미지 데이터인 숫자 1을 Auto Encoder 모델에 넣은 후 결과값으로 입력 데이터와 비슷한 손글씨 숫자 이미지 1을 출력하는 그림이다. 입력 데이터인 784개의 뉴런들을 500개, 300개, 2개로 압축시킴으로써 입력 데이터의 대표적인 특성을 추출한다. 그리고 이를 기반으로 다시 대칭적인 구조로 300개, 500개 뉴런으로 확장시킨 후 최종적으로 입력 데이터와 똑같은 사이즈인 784개의 뉴런 개수로 최종 값을 출력시킨다. 그렇게 해서 나온 결과 데이터가 그림의 오른쪽에 살짝 희미한 이미지 데이터이다.

Auto Encoder에서 압축시키는 부분은 Encoder 라고 하며 확장시키는 부분은 Decoder라고 부른다. 참고로 Encoder 또는 Decoder 둘 중 하나의 파라미터를 고정시키고 나머지 부분만 학습시키는 경우도 있다. 둘 중 한 부분만을 이용하되 전체적인 Encoder - Decoder 구조는 유지해야 한다.

예를 들어 아래 그림처럼 hidden layer의 뉴런 수를 input layer(입력층) 보다 작게해서 데이터를 압축(차원을 축소)한다거나, 입력 데이터에 노이즈(noise)를 추가한 후 원본 입력을 복원할 수 있도록 네트워크를 학습시키는 등 다양한 오토인코더가 있다. 이러한 제약들은 오토인코더가 단순히 입력을 바로 출력으로 복사하지 못하도록 방지하며, 데이터를 효율적으로 표현(representation)하는 방법을 학습하도록 제어한다.

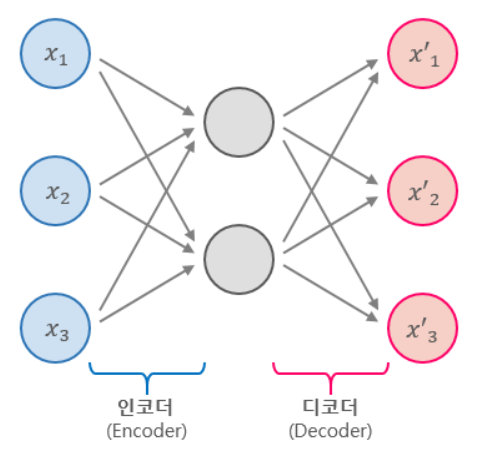
오토인코더는 위의 그림에서 볼 수 있듯이 항상 인코더(encoder)와 디코더(decoder), 두 부분으로 구성되어 있다.

• 인코더(encoder) : 인지 네트워크(recognition network)라고도 하며, 입력을 내부 표현으로 변환한다.
• 디코더(decoder) : 생성 네트워크(generative nework)라고도 하며, 내부 표현을 출력으로 변환한다.
  
  

오토인코더는 위의 그림에서 처럼, 입력과 출력층의 뉴런 수가 동일하다는 것만 제외하면 일반적인 MLP(Multi-Layer Perceptron)과 동일한 구조이다. 오토인코더는 입력을 재구성하기 때문에 출력을 재구성(reconstruction)이라고도 하며, 손실함수는 입력과 재구성(출력)의 차이를 가지고 계산한다.

Undercomplete AE

위 그림의 오토인토더는 히든 레이어의 뉴런(노드, 유닛)이 입력층보다 작으므로 입력이 저차원으로 표현되는데, 이러한 오토인코더를 Undercomplete Autoencoder라고 한다. undercomplete 오토인코더는 저차원을 가지는 히든 레이어에 의해 입력을 그대로 출력으로 복사할 수 없기 때문에, 출력이 입력과 같은 것을 출력하기 위해 학습해야 한다. 이러한 학습을 통해 undercomplete 오토인코더는 입력 데이터에서 가장 중요한 특성(feature)을 학습하도록 만든다.

PCA 구현

위에서 살펴본 Undercomplete 오토인코더에서 활성화 함수를 sigmoid, ReLU같은 비선형(non-linear)함수가 아니라 선형(linear) 함수를 사용하고, 손실함수로 MSE(Mean Squared Error)를 사용할 경우에는 PCA라고 볼 수 있다.


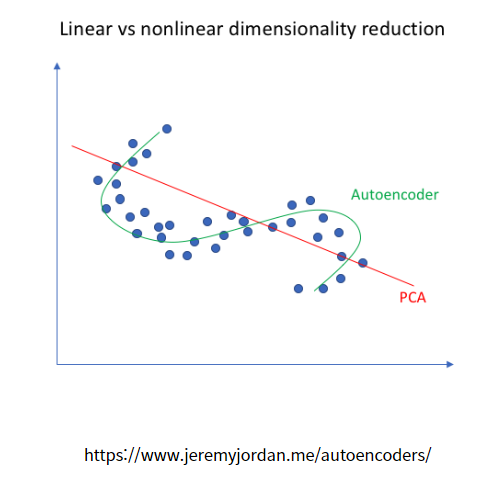
기본적으로 PCA는 선형적으로 데이터 차원을 감소시켜 준다. 위 그림에서 보는 것처럼 빨간색 실선이 PCA를 뜻한다. 데이터가 주어졌을 때 위와 같이 선형적으로 데이터의 차원을 축소시키게 된다. 반면에 초록색 실선인 Auto Encoder의 Encoder는 비선형적으로 데이터의 차원을 줄여줄 수 있다.

PCA는 보통 선형적으로 데이터 차원을 축소하고 비선형적으로 데이터를 축소하기 위해서는 Auto Encoder를 사용한다.



Auto Encoder의 Encoder 부분은 입력 데이터를 압축하는 과정에서 데이터의 차원을 축소시킨다. 차원의 축소 관점에서 Encoder 부분은 주성분 분석인 PCA(Principal Component Analysis)와 유사한 점이 있다. 차원의 축소는 결국 특징을 뽑아낸다는 것을 의미하는데, 다음 그림을 살펴보자.

아래의 예제코드는 가상의 3차원 데이터셋을 undercomplete 오토인코더를 사용해 2차원으로 축소하는 PCA를 수행한 코드이다.

# 3D 데이터셋을 만듦
import numpy.random as rnd

rnd.seed(4)
m = 200
w1, w2 = 0.1, 0.3
noise = 0.1

angles = rnd.rand(m) * 3 * np.pi / 2 - 0.5
data = np.empty((m, 3))
data[:, 0] = np.cos(angles) + np.sin(angles)/2 + noise * rnd.randn(m) / 2
data[:, 1] = np.sin(angles) * 0.7 + noise * rnd.randn(m) / 2
data[:, 2] = data[:, 0] * w1 + data[:, 1] * w2 + noise * rnd.randn(m)

# 데이터 정규화
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train = scaler.fit_transform(data[:100])
X_test = scaler.transform(data[100:])

reset_graph()

################
# layer params #
################
n_inputs = 3
n_hidden = 2  # coding units
n_outputs = n_inputs

# autoencoder
X = tf.placeholder(tf.float32, shape=[None, n_inputs])
hidden = tf.layers.dense(X, n_hidden)
outputs = tf.layers.dense(hidden, n_outputs)

################
# Train params #
################
learning_rate = 0.01
n_iterations = 1000
pca = hidden

# loss
reconstruction_loss = tf.reduce_mean(tf.square(outputs - X))  # MSE
# optimizer
train_op = tf.train.AdamOptimizer(learning_rate).minimize(reconstruction_loss)

with tf.Session() as sess:
    tf.global_variables_initializer().run()
    for iteration in range(n_iterations):
        train_op.run(feed_dict={X: X_train})
    pca_val = pca.eval(feed_dict={X: X_test})

# fig = plt.figure(figsize=(4,3))
# plt.plot(pca_val[:,0], pca_val[:, 1], "b.")
# plt.xlabel("$z_1$", fontsize=18)
# plt.ylabel("$z_2$", fontsize=18, rotation=0)
# print('pca_val.shape :', pca_val.shape)
# plt.show()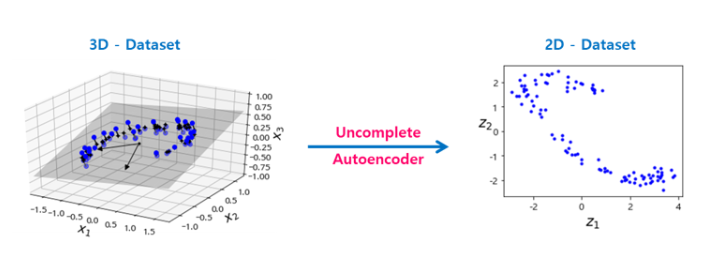

위의 코드에서 입력의 개수(n_inputs)와 출력의 개수(n_outputs)가 동일한 것을 알 수 있으며, PCA를 위해 tf.layers.dense()에서 따로 활성화 함수를 지정해주지 않아 모든 뉴런이 선형인 것을 알 수 있다.

Stacked AE

Stacked 오토인코더 또는 deep 오토인코더는 여러개의 히든 레이어를 가지는 오토인코더이며, 레이어를 추가할수록 오토인코더가 더 복잡한 코딩(부호화)을 학습할 수 있다. stacked 오토인코더의 구조는 아래의 그림과 같이 가운데 히든레이어(코딩층)을 기준으로 대칭인 구조를 가진다.

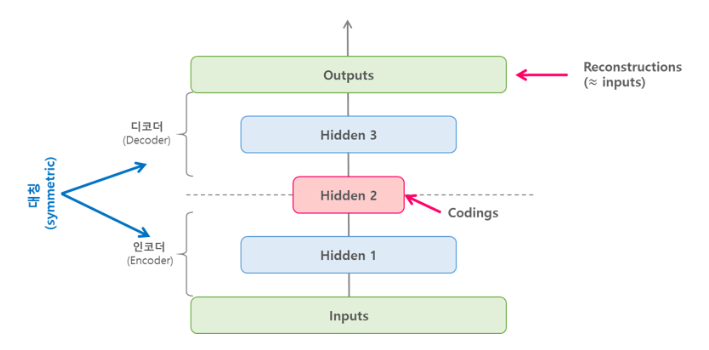
딥러닝 모델을 구축 시에 중요한 것 중 하나는 딥러닝 노드, 레이어의 개수 등 하이퍼파라미터 종류가 다양하다는 것이다. 이 중 Auto Encoder를 모델링할 때는 우선 Encoded layer(codings)의 노드 개수를 1차적으로 적절히 설정한 후 Layer2, Layer1 노드 개수를 설정하는 순서로 진행하는 것이 바람직하다.

• 압축하는 이유

"그렇다면 입력 데이터를 압축하지 않고 사이즈를 유지한 채 출력 데이터로 그대로 내보내면 가장 입력 데이터와 동일하지 않을까?"
물론 그렇게 설정할 수 있다 !
하지만 우리가 원하는 것은 입력 데이터를 압축시킴으로써 얻는 내재된(Latent) 정보를 얻기 위한 것이다. 또한 Auto Encoder는 양이 큰 데이터를 축소시켜 전달하는 역할을 하기도 한다. 따라서 압축을 하지 않는 것은 Auto Encoder의 근본적인 목적에 부합하지 않기 때문에 해당 방법은 고려할 만하지 않다.

Stacked Auto Encoder는 Unsupervised pre-training으로 활용될 수 있다. 여기서는 간단히 소개하고 넘어가겠다. pre-training이란, 이미 학습된 다른 모델의 파라미터를 그대로 가져가서 사용하는 것을 말한다.

구현 with TensorFlow

Stacked 오토인코더는 기본적인 Deep MLP와 비슷하게 구현할 수 있다. 아래의 예제는 He 초기화, ELU 활성화 함수, l2 규제(regularization)을 사용해 MNIST 데이터셋에 대한 stacked 오토인코더를 구현한 코드이다.

• MNIST Data Load

(train_x, train_y), (test_x, test_y) = tf.keras.datasets.mnist.load_data()
train_x = train_x.astype(np.float32).reshape(-1, 28*28) / 255.0
test_x = test_x.astype(np.float32).reshape(-1, 28*28) / 255.0
train_y = train_y.astype(np.int32)
test_y = test_y.astype(np.int32)
valid_x, train_x = train_x[:5000], train_x[5000:]
valid_y, train_y = train_y[:5000], train_y[5000:]

# Mini-batch
def shuffle_batch(features, labels, batch_size):
    rnd_idx = np.random.permutation(len(features))
    n_batches = len(features) // batch_size
    for batch_idx in np.array_split(rnd_idx, n_batches):
        batch_x, batch_y = features[batch_idx], labels[batch_idx]
        yield batch_x, batch_y

• 학습

reset_graph()

from functools import partial

################
# layer params #
################
n_inputs = 28 * 28
n_hidden1 = 300  # encoder
n_hidden2 = 150  # coding units
n_hidden3 = n_hidden1  # decoder
n_outputs = n_inputs  # reconstruction

################
# train params #
################
learning_rate = 0.01
l2_reg = 0.0001
n_epochs = 5
batch_size = 150
n_batches = len(train_x) // batch_size

# set the layers using partial
he_init = tf.keras.initializers.he_normal()  # He 초기화
l2_regularizer = tf.contrib.layers.l2_regularizer(scale=l2_reg)  # L2 규제
dense_layer = partial(tf.layers.dense,
                      activation=tf.nn.elu,
                      kernel_initializer=he_init,
                      kernel_regularizer=l2_regularizer)

# stacked autoencoder
inputs = tf.placeholder(tf.float32, shape=[None, n_inputs])

hidden1 = dense_layer(inputs, n_hidden1)
hidden2 = dense_layer(hidden1, n_hidden2)
hidden3 = dense_layer(hidden2, n_hidden3)
outputs = dense_layer(hidden3, n_outputs, activation=None)

# loss
reconstruction_loss = tf.reduce_mean(tf.square(outputs - inputs))
reg_losses = tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)
loss = tf.add_n([reconstruction_loss] + reg_losses)

# optimizer
train_op = tf.train.AdamOptimizer(learning_rate).minimize(loss)

# Saver
saver = tf.train.Saver(max_to_keep=1)

%%time
with tf.Session() as sess:
    tf.global_variables_initializer().run()
    for epoch in range(n_epochs):
        for iteration in range(n_batches):
            batch_x, batch_y = next(shuffle_batch(train_x, train_y, batch_size))
            sess.run(train_op, feed_dict={inputs: batch_x})
        loss_train = reconstruction_loss.eval(feed_dict={inputs: batch_x})
        print('epoch : {}, Train MSE : {:.5f}'.format(epoch, loss_train))
    saver.save(sess, './model/stacked_ae.ckpt')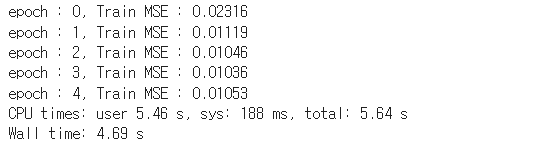

def show_reconstructed_digits(X, outputs, model_path=None, n_test_digits=2):
    with tf.Session() as sess:
        if model_path:
            saver.restore(sess, model_path)
        outputs_val = outputs.eval(feed_dict={inputs: test_x[:n_test_digits]})

    fig = plt.figure(figsize=(10, 4))
    for digit_index in range(n_test_digits):
        plt.subplot(n_test_digits, 2, digit_index * 2 + 1)
        plot_image(test_x[digit_index])
        plt.subplot(n_test_digits, 2, digit_index * 2 + 2)
        plot_image(outputs_val[digit_index])
        
# show_reconstructed_digits(inputs, outputs, './model/stacked_ae.ckpt')

위의 코드를 학습 시킨 후에 테스트셋의 일부를 재구성하였을 때, 아래의 그림과 같은 결과가 나온다.

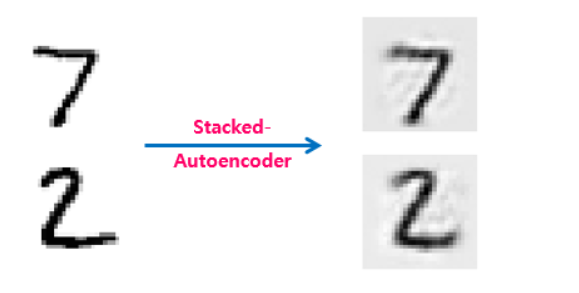
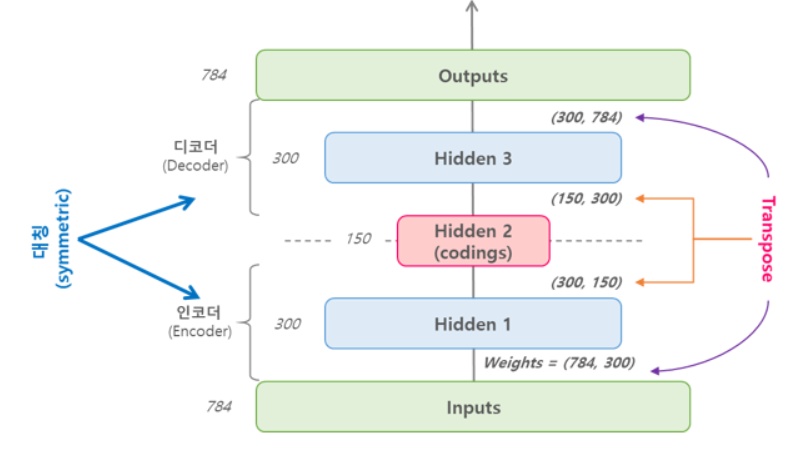
가중치 묶기

위(3.1)에서 구현한 stacked 오토인코더처럼, 오토인코더가 완전히 대칭일 때에는 일반적으로 인코더(encoder)의 가중치와 디코더(decoder)의 가중치를 묶어준다. 이렇게 가중치를 묶어주게 되면, 네트워크의 가중치 수가 절반으로 줄어들기 때문에 학습 속도를 높이고 오버피팅의 위험을 줄여준다.

한 번에 한 층씩 학습하기

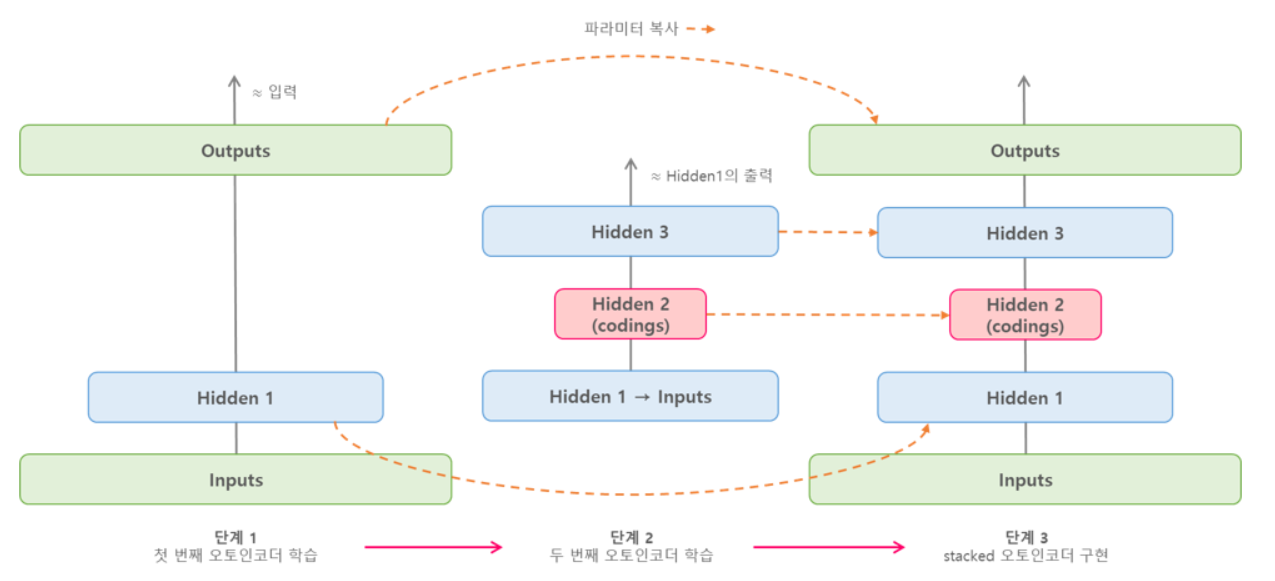
위와 같이 한 번에 전체 오토인코더를 학습시키는 것보다 아래의 그림처럼 한 번에 오토인코더 하나를 학습하고, 이를 쌓아올려서 한 개의 stacked-오토인코더를 만드는 것이 훨씬 빠르며 이러한 방식은 아주 깊은 오토인코더일 경우에 유용하다.

• [단계 1]에서 첫 번째 오토인코더는 입력을 재구성하도록 학습된다.

• [단계 2]에서는 두 번째 오토인코더가 첫 번째 히든 레이어(Hidden 1)의 출력을 재구성하도록 학습된다.

• [단계 3]에서는 단계1 ~ 2의 오토인코더를 합쳐 최종적으로 하나의 stacked-오토인코더를 구현한다.

텐서플로에서 이렇게 여러 단계의 오토인코더를 학습시키는 방법으로는 다음과 같이 두 가지 방법이 있다.

• 각 단계마다 다른 텐서플로 그래프(graph)를 사용하는 방법

• 하나의 그래프에 각 단계의 학습을 수행하는 방법

  
  

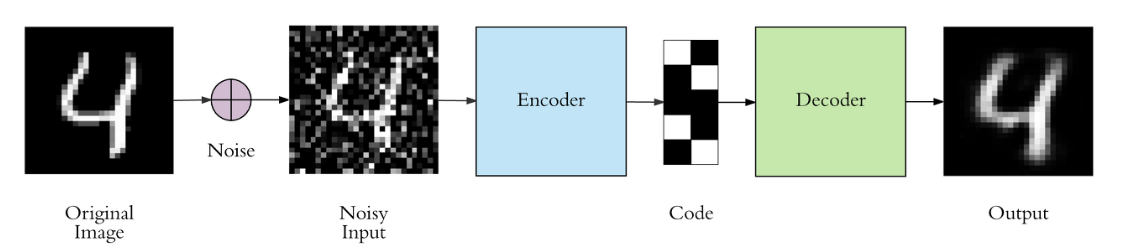
Denoising AE

오토인코더가 의미있는 특성(feature)을 학습하도록 제약을 주는 다른 방법은 입력에 노이즈(noise, 잡음)를 추가하고, 노이즈가 없는 원본 입력을 재구성하도록 학습시키는 것이다. 노이즈는 아래의 그림처럼 입력에 가우시안(Gaussian) 노이즈를 추가하거나, 드롭아웃(dropout)처럼 랜덤하게 입력 유닛(노드)를 꺼서 발생 시킬 수 있다.

가우시안 노이즈 추가

https://towardsdatascience.com/applied-deep-learning-part-3-autoencoders-1c083af4d798?gi=b93263c1ab82

깨끗한 원본 이미지에 Gaussian 분포에서 샘플링한 임의의 노이즈 데이터를 원본 이미지에 첨가한다.

왜 깨끗한 이미지에 일부러 노이즈를 첨가하는 것일까 ?

왜냐하면!

학습 데이터는 위의 Original Image같이 깨끗한 이미지겠지만 실제 낯선 환경의 실제 Test 데이터는 노이즈가 첨가되어 있는 지저분한 데이터일 수 있기 때문이다.

만약 깨끗한 원본 이미지 데이터로만 모델이 학습됐다면 노이즈가 첨가된 데이터가 들어왔을 시 원본 이미지를 제대로 복구시키지 못하는 일종의 Overfitting 문제를 야기할 것이다.

하지만 Gaussian 분포에서 샘플링하는 노이즈는 학습할 때마다 노이즈 데이터가 바뀔 것이고 이렇게 계속적인 학습이 이루어진다면 모델은 다양한 노이즈가 첨가된 데이터들을 학습시키게 된다. 결국 모델의 Regularization(일반화) 효과를 낸다.
따라서 혹여나 '더러운 데이터' 즉, 노이즈가 첨가된 데이터가 들어왔을 경우를 대비해서 모델이 스스로 잘 복구시키도록 일부러 원본 이미지에 노이즈를 첨가한 후 모델을 학습시키는 것이다.

Dropout

Dropout은 사전에 정의한 확률로 노드의 일부 개수를 삭제해버린다. 따라서 이미지 데이터로 예를 들자면 이미지 픽셀의 일부가 사라지는 것이다. 이는 Gaussian 노이즈를 첨가한 후 효과와 동일하게 Overfitting을 예방하는 Regularization(일반화) 효과를 일으킨다.

Sparse AE

오토인코더가 좋은 특성을 추출하도록 만드는 다른 제약 방법은 희소성(sparsity)를 이용하는 것인데, 이러한 오토인코더를 Sparse Autoencoder라고 한다. 이 방법은 손실함수에 적절한 항을 추가하여 오토인코더가 코딩층(coding layer, 가운데 층)에서 활성화되는 뉴런 수를 감소시키는 것이다.

예를 들어 코딩층에서 평균적으로 5% 뉴런만 활성화되도록 만들어 주게 되면, 오토인코더는 5%의 뉴런을 조합하여 입력을 재구성해야하기 때문에 유용한 특성을 표현하게 된다.


이러한 Sparse-오토인코더를 만들기 위해서는 먼저 학습 단계에서 코딩층의 실제 sparse(희소) 정도를 측정해야 하는데, 전체 학습 배치(batch)에 대해 코딩층의 평균적인 활성화를 계산한다. 배치의 크기는 너무 작지 않게 설정 해준다.

위에서 각 뉴런에 대한 평균 활성화 정도를 계산하여 구하고, 손실함수에 희소 손실(sparsity loss)를 추가하여 뉴런이 크게 활성화 되지 않도록 규제할 수 있다.

예를 들어 한 뉴런의 평균 활성화가 0.3이고 목표 희소 정도가 0.1이라면, 이 뉴런은 덜 활성화 되도록 해야한다. 희소 손실을 구하는 간단한 방법으로는 제곱 오차
를 추가하는 방법이 있다. 하지만, Sparse-오토인코더에서는 아래의 그래프 처럼 MSE보다 더 경사가 급한 쿨백 라이블러 발산(KL-divergense, Kullback-Leibler divergense)을 사용한다.

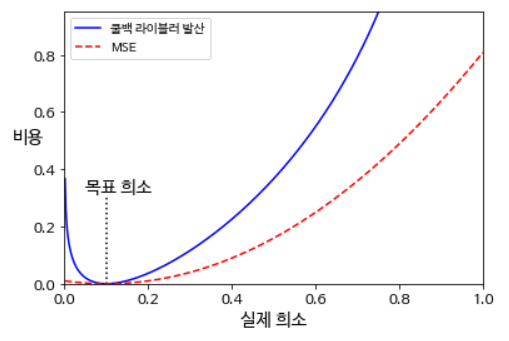
KL-Divergense

쿨백-라이블러 발산(Kullback-Leibler divergence, KLD)은 두 확률분포의 차이를 계산하는 데 사용하는 함수이다. 딥러닝 모델을 만들 때 예로 들면 우리가 가지고 있는 데이터의 분포 P(x)와 모델이 추정한 데이터의 분포 Q(x) 간에 차이를 KLD를 활용해 구할 수 있다. KLD의 식은 다음과 같이 정의된다.

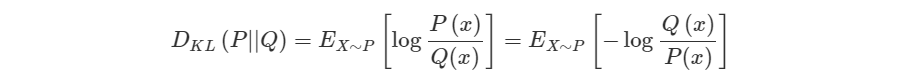
P와 Q가 동일한 확률분포일 경우 KLD는 정의에 따라 그 값이 0이 된다. 하지만 KLD는 비대칭(not symmetric)으로 P와 Q 위치가 뒤바뀌면 KLD 값도 달라집니다. 따라서 KLD는 거리함수로는 사용할 수 없다.

Sparse-오토인코더에서는 코딩층에서 뉴런이 활성화될 목표 확률 와 실제확률 (학습 배치에 대한 평균 활성화) 사이의 발산을 측정하며, 식은 다음과 같다.

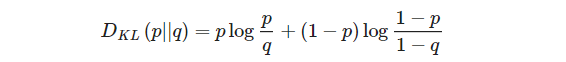
위의 식을 이용해 코딩층의 각 뉴런에 대해 희소 손실을 구하고 이 손실을 모두 합한 뒤 희소 가중치 하이퍼파라미터를 곱하여 손실함수의 결과에 더해준다.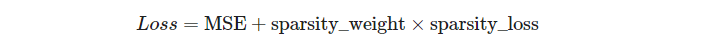

• Tensorflow 구현

reset_graph()

################
# layer params #
################
noise_level = 1.0
n_inputs = 28 * 28
n_hidden1 = 1000 # sparsity coding units
n_outputs = n_inputs

################
# train params #
################
sparsity_target = 0.1  # p
sparsity_weight = 0.2
learning_rate = 0.01
n_epochs = 20
batch_size = 1000

def kl_divergence(p, q):
    # 쿨백 라이블러 발산
    return p * tf.log(p / q) + (1 - p) * tf.log((1 - p) / (1 - q))

inputs = tf.placeholder(tf.float32, shape=[None, n_inputs])

hidden1 = tf.layers.dense(inputs, n_hidden1, activation=tf.nn.sigmoid)
outputs = tf.layers.dense(hidden1, n_outputs)

# loss
hidden1_mean = tf.reduce_mean(hidden1, axis=0)  # 배치 평균  == q
sparsity_loss = tf.reduce_sum(kl_divergence(sparsity_target, hidden1_mean))
reconstruction_loss = tf.losses.mean_squared_error(labels=inputs, predictions=outputs)
loss = reconstruction_loss + sparsity_weight * sparsity_loss

# optimizer
train_op = tf.train.AdamOptimizer(learning_rate).minimize(loss)

# saver
saver = tf.train.Saver()

# Train
with tf.Session() as sess:
    tf.global_variables_initializer().run()
    n_batches = len(train_x) // batch_size
    for epoch in range(n_epochs):
        for iteration in range(n_batches):
            print("\r{}%".format(100 * iteration // n_batches), end="")
            sys.stdout.flush()
            batch_x, batch_y = next(shuffle_batch(train_x, train_y, batch_size))
            sess.run(train_op, feed_dict={inputs: batch_x})
        recon_loss_val, sparsity_loss_val, loss_val = sess.run([reconstruction_loss, 
                                                                sparsity_loss,
                                                                loss], feed_dict={inputs: batch_x})
        print('\repoch : {}, Train MSE : {:.5f},'.format(epoch, recon_loss_val),
               'sparsity_loss : {:.5f}, total_loss : {:.5f}'.format(sparsity_loss_val, loss_val))
    saver.save(sess, './model/my_model_sparse.ckpt')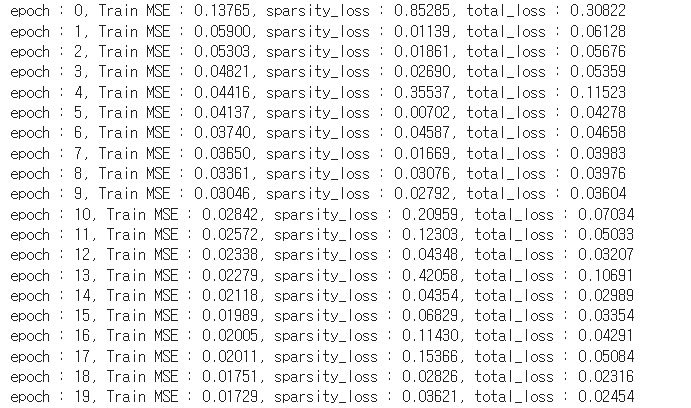

show_reconstructed_digits(inputs, outputs, "./model/my_model_sparse.ckpt")

Variational AutoEncoder (VAE)

VAE(Variational AutoEncoder)는 2014년 D.Kingma와 M.Welling이 Auto-Encoding Variational Bayes 논문에서 제안한 오토인코더의 한 종류이다. VAE는 위에서 살펴본 오터인코더와는 다음과 같은 다른점이 있다.

• VAE는 확률적 오토인코더(probabilistic autoencoder)다. 즉, 학습이 끝난 후에도 출력이 부분적으로 우연에 의해 결정된다.
• VAE는 생성 오토인코더(generative autoencoder)이며, 학습 데이터셋에서 샘플링된 것과 같은 새로운 샘플을 생성할 수 있다.

VAE의 구조는 아래의 그림과 같다.

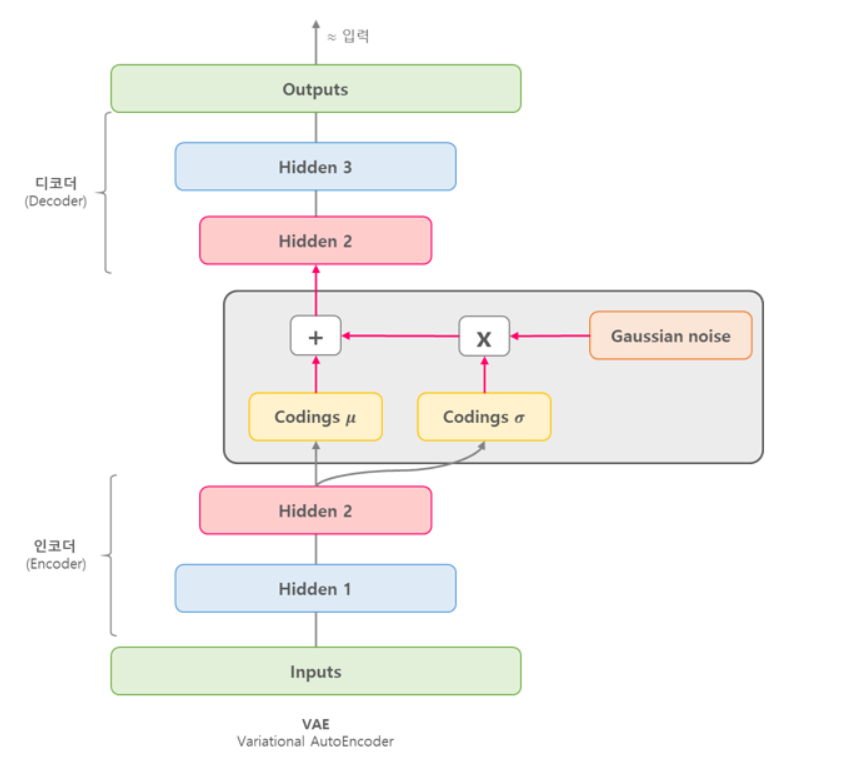
VAE의 코딩층은 다른 오토인코더와는 다른 부분이 있는데 주어진 입력에 대해 바로 코딩을 만드는 것이 아니라, 인코더(encoder)는 평균 코딩 와 표준편차 코딩 을 만든다. 실제 코딩은 평균이 이고 표준편차가 인 가우시안 분포(gaussian distribution)에서 랜덤하게 샘플링되며, 이렇게 샘플링된 코딩을 디코더(decoder)가 원본 입력으로 재구성하게 된다.

VAE는 마치 가우시안 분포에서 샘플링된 것처럼 보이는 코딩을 만드는 경향이 있는데, 학습하는 동안 손실함수가 코딩(coding)을 가우시안 샘플들의 집합처럼 보이는 형태를 가진 코딩 공간(coding space) 또는 잠재 변수 공간(latent space)로 이동시키기 때문이다.

이러한 이유로 VAE는 학습이 끝난 후에 새로운 샘플을 가우시안 분포로 부터 랜덤한 코딩을 샘플링해 디코딩해서 생성할 수 있다.

VAE의 손실함수

VAE의 손실함수는 두 부분으로 구성되어 있다. 첫 번째는 오토인코더가 입력을 재구성하도록 만드는 일반적인 재구성 손실(reconstruction loss)이고, 두 번째는 가우시안 분포에서 샘플된 것 샅은 코딩을 가지도록 오토인코더를 제어하는 latent loss이다.