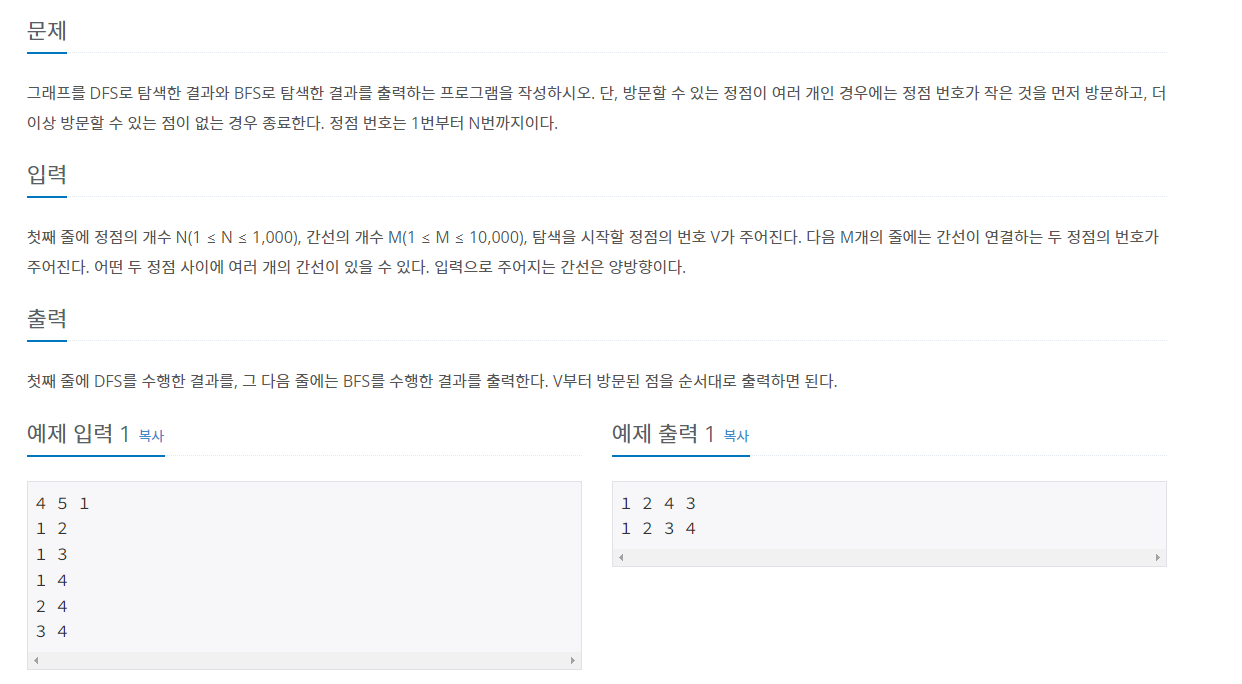
DFS와 BFS를 공부하기 좋은 문제인것 같다.
알고리즘을 공부하면서 DFS와 BFS가 무엇인지는 알았지만 정작, 파이썬으로 구현할줄은 몰랐다.
그래서 이 문제를 통해 DFS와 BFS에 대해 정확히 알아가고 싶다.
먼저 DFS는 깊이우선탐색으로 아래 그림 처럼 연결된 하위 노드가 있으면 우선적으로 하위 노드들을 탐색한다.
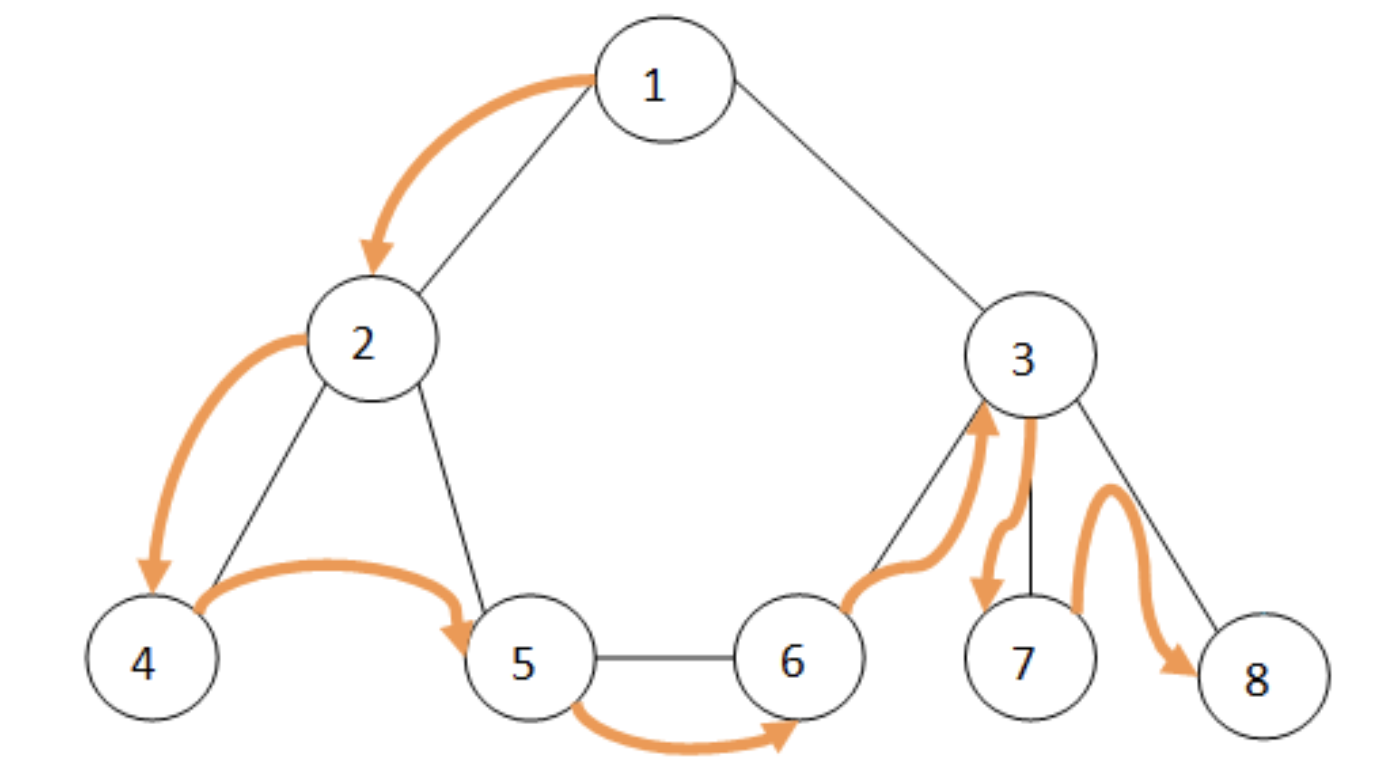
반면에, BFS는 너비우선탐색으로 같은 레벨의 노드를 우선적으로 탐색한다.
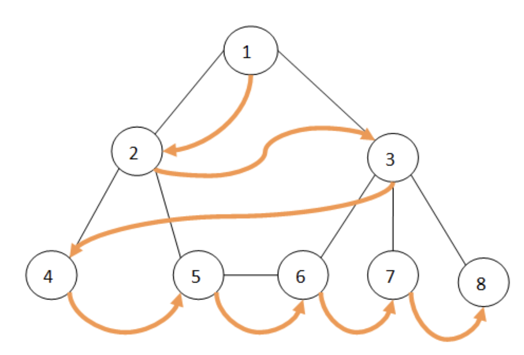
DFS와 BFS를 구현하기에 앞서, 탐색할 트리는 보통 리스트로 구현한다.
tree = [[False] * N for _ in range(M)]tree[N]의 리스트가 M개 존재하는 것이다. 그래서 노드 1번과 연결된 노드는 tree[1]에 저장돼있다.
DFS와BFS 문제를 해결하기에 앞서 먼저 입력된 트리를 리스트에 저장하고 연결된 노드를 표시해야한다. 위에서는 False로 했지만, 1이나 0 .. 등 여러가지로 표현하는 방법이 있다.
BFS
보통 queue를 통하여 구현한다. BFS를 구현한 함수를 bfs라 하고 매개변수로 시작노드를 받는다고 하자.
bfs(시작노드) <시작노드 : 보통 1번 노드>
전달받은 시작노드를 queue(이하 q)에 저장한다.
현재 q 상태는 q = [1]이다
시작 노드를 방문처리한다.
별도의 방문처리를 담당하는 1차원 리스트를 선언하고 False로 처리하며, 방문한 노드의 index를 True로 변경함으로써 방문한 노드를 구별한다.
이제 q에 들어 있는 노드를 popleft(이하 pop)한다. 이하 과정부터는 q가 비워진 상태일까지 한다.
이하 과정은 모두 while q : 에 속해 q가 비워질 때 까지 반복문이 돌아간다.pop하면서 원하는 작업을 실행하면 된다. 이 문제에서는 pop한 노드의 번호를 출력하면 된다.
현재 q 상태는 q = [1]이다
아까 만들어 놓은 트리를 이용하여 bfs를 실시하면 된다 -> tree [ q에서 pop된 노드 번호 ]를 이용하여 for 반복문을 돌린다.
이미 tree에는 노드의 연결 상태가 모두 저장되어있기 때문에 방문처리가 가능하다.
그림을 예로 들면 이미 tree[1]에는 [2,3]의 노드 번호가 저장되어있다.
tree[1]에서 반복문을 돌면서 방문 하지 않은 노드라면 q에 추가하고 방문 처리를 해준다.
대략적으로,
for tree[ q에서 pop된 노드 번호 ] :
if 방문 안함 :
q에 append
해당 노드 방문처리이런 과정을 겪는다.
1번 노드가 pop되고 bfs를 한 번 돌린 q의 상태는 q = [ 2, 3 ] 이다.
현재 방문 처리된 노드는 1, 2, 3번 노드이다.
아직 q에는 값이 들어 있으므로 다시 q에서 pop(popleft)부터 시작하는 과정이 반복된다. q에 저장된 1번 노드와 연결된 노드의 하위 노드들을 bfs하는 것이다.
2번 노드가 pop되고 tree[2]에서 반복문을 돌린다.
! 여기서 방문처리 하는 이유가 나온다. 2번 노드는 1번 노드와도 연결되어 있으므로 현재 tree[2]에 1번 노드가 저장되어 있기 때문에 1번 노드에 대하여 방문처리를 하지않으면 또 다시 1번노드가 q에 append되고 무한루프에 빠지게된다. !
1번 노드는 방문 처리됐으므로 q에 append하지 않는다. 2번과 연결된 4번과 5번 노드는 방문하지 않은 노드이므로 q에 append하고 방문처리한다.
q의 현재 상태는 = [ 3, 4, 5 ]이며,
방문처리된 노드는 1, 2, 3, 4, 5번 노드이다.
이후 과정을 계속 반복한다. q가 FIFO (First In First Out) 구조이므로 같은 레벨의 노드가 먼저 pop되고 하위 레벨의 노드는 나중에 pop되기 때문에 bfs, 너비우선탐색이 가능하다.
DFS
재귀함수를 통하여 구현가능하다. DFS를 구현한 함수를 dfs라하고 매개변수로 시작노드를 받는다고 하자.
dfs(시작노드) <시작노드 : 보통 1번 노드>
전달받은 시작노드를 방문 처리한다. 그리고 BFS와 마찬가지로 tree[ 노드 번호 ]에서 for반복문을 돌린다. 방문 하지 않은 노드라면 방문처리하고 dfs[ 해당 노드 ]를 호출한다.
dfs(1) -> tree[1] = { 2, 3 }
dfs(2) -> tree[2] = { 4 , 5 }
dfs(4) -> tree[4] ={ x }
dfs(5) -> tree[5] = { 6 }
dfs(6) -> tree[6] = { 3 }
dfs(3) -> tree[3] = { 7 , 8 }
dfs(7) -> tree[7] = { x }
dfs(8) -> tree[8] = { x }
위 과정이 그림에 해당하는 dfs호출 순서이며 곧, dfs의 탐색순서이다.
완성된 코드는 여기서 보면 된다.
완성된 코드