백준 - 2178 미로 탐색

2178 미로 탐색

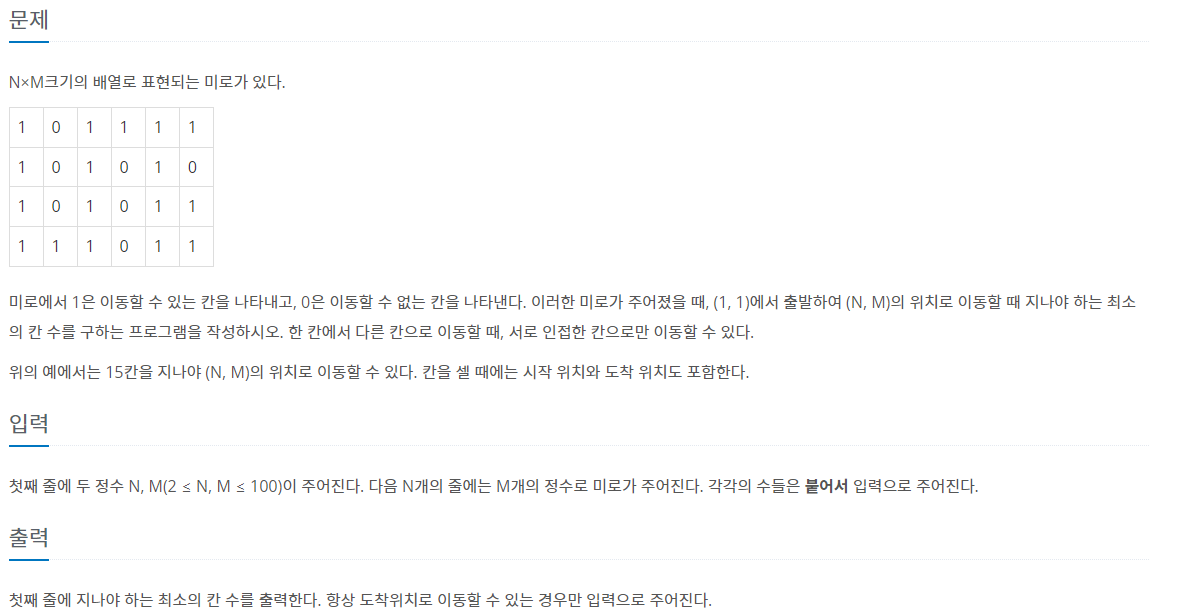
전형적인 길찾기 문제로 최단거리를 구하는 문제이다. 따라서 BFS를 쓰는 것이 좋다

DFS로도 풀 수 있지만 BFS로 했을 때 정답의 경로가 발견이 되자마자 탐색을 종료하기 떄문에 운이 좋으면 같은 완전탐색인 DFS보다 시간을 더 단축시킬 수 있다.

---

위 문제 처럼 격자 칸이 주어지고 사방으로 움직이면서 길을 찾는 문제들은 자주 출제되는 형태의 문제이다.

이 문제를 공부하면서 중요한 포인트라고 생각되는 것은 아래와 같다.

1. dx,dy의 상대좌표를 이용하여 움직이는 좌표 계산하기
2. N x M 격자 좌표에서 유효성 검사하기
3. 격자칸을 좌표계로 대입할 때 주의하기
   • x 좌표계는 dy , y좌표계는 dx이다
     [0][1] -> (1,0)
     [0][2] -> (2,0)
     [1][3] -> (3,1)
     [2][3] -> (3,2)
4. bfs로 탐색하는 것은 좌표의 이동이다 = 위 아래 왼쪽 오른쪽
   -for k in range(4) => 4가지 방향... 8가지 방향이면 8번 반복

---

먼저 격자칸을 리스트에 저장하고 N x M 크기를 가지는 방문 체크 용도의 리스트를 선언하고 False로 초기화한다.

또한 격자칸은 N x M으로 크기가 정해져 있으므로 이 크기를 벗어나면 안된다.

따라서 별도의 격자칸을 벗어나는지 확인해주는 함수를 만들어준다

def vaildBoard(y,x) :
	return 0<=y<N and 0<=x<M

좌표의 움직임을 dx,dy를 이용해서 상대좌표로 나타낼 것이다.

dx = (1,0,-1,0) 
dy = (-1,0,1,0)

BFS를 사용해 문제를 해결할 것이므로 deque(q)를 사용한다.

시작좌표와 최단거리를 구해야하므로 거리(d)를 q에 append하고 시작 좌표를 방문체크한다.

q가 빌 때 까지 반복한다. q에는 현재 (0,0,1)이 저장되어있다.

이 시작 좌표와 거리를 q에서 popleft한다.

해당 좌표가 N,M이면 거리를 출력하면 된다.

아니라면 bfs탐색을 시작한다.

공부했던 bfs는 그래프를 탐색하므로 각 tree[ 노드 번호 ] 였지만 이 문제는 미로의 탐색이다. 사람이 격자칸 미로를 움직인다고 생각하면 이 사람이 미로를 탐색하면서 이동 할 수 있는 방향은 4가지 이다. 따라서 사람이 이동할 수 있는 4가지 방향에 대해서 bfs탐색을 돌린다.

for y,x,d in range(4) : #4가지 방향
	ny = y + dy[k] 
    nx = x + dx[k]
    nd = d + 1

ny와nx는 이동한 후에 좌표이다. 움직이는 좌표를 상대좌표를 이용해서 구한다고 했는데, dy,dx 리스트에 들어있는 1,-1을 이용해서 4가지 방향으로 이동한 좌표를 구한다.

좌표가 이동한 후에 방문을 한 좌표인지, 유효한 좌표인지 확인한다. 후에 q에 움직인 좌표 +1한 거리를 q에 넣어주고 방문체크를 해준다.

백준에 제출한 코드

import sys
from collections import deque

dx = (1,0,-1,0)
dy = (0,1,0,-1)

N,M = map(int, sys.stdin.readline().split())

board = [sys.stdin.readline() for _ in range(N)]
visitChk = [[False] *  M for _ in range(N)]
dq = deque()
dq.append((0,0,1))
visitChk[0][0] = True

def endChk(y,x) :
    return 0<=y<N and 0<=x<M

while len(dq)>0 :
    y,x,d = dq.popleft()

    if y == N-1 and x==M-1 :
        print(d)
        break

    for k in range(4) :
        ny = y + dy[k]
        nx = x + dx[k]
        nd = d + 1
        if endChk(ny,nx) and not visitChk[ny][nx] and board[ny][nx] == "1" :
            visitChk[ny][nx] = True
            dq.append((ny,nx,nd))