벡터와 스칼라의 연산

그림의 x와 c를 파이썬으로 표현해보자.

생성한 배열이 몇행 몇열인지 확인하기
a.shape
튜플로 출력 (2,3) => 2x3
- Array Indexing
파이썬의 리스트와 유사하게 진행
파이썬 리스트의 경우 2차원 행렬의 [0행 1열]을 불러오는 경우 w[0][1] 라고 쓰지만, numpy의 array의 경우 w[0,1] 라고 쓴다.
리스트 : w[0][1] <---> numpy :w[0,1]
- Array Slicing
파이썬의 slicing과 유사하게 진행
w = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
w = 1 2 3 4
5 6 7 8
9 10 11 12
w에서 2,3과 6,7을 추출하고 싶을때,
파이썬 ⏩ w[0: 2][1: 3]
numpy array ⏩w[0:2, 1:3]
📛주의📛 전체 행이더라도 꼭 : 를 써야한다! w[ , 1:3] << : 을 안 쓰면 오류 발생
- Array Broadcasting
numpy의 특수 연산 규칙
1. 차원이 다른 두 행렬의 합
M x N 1 x N
행렬에서 차원이 다른 두 행렬을 더할 수 없다.
하지만 numpy에서는 더할 수 있다.
두 행렬을 더할 때 numpy에서 [1 0 1] 을 M번 복제한 후 원소끼리 더한다.
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
b = np.array([[1, 0, 1]])
a + b
array([[ 2, 2, 4],
[ 5, 5, 7],
[ 8, 8, 10]])
2. 차원이 다른 두 행렬의 곱
M x N 1 x N
행렬에서 차원이 다른 두 행렬을 곱할 수는 있다 (조건이 붙긴 하지만..) numpy에서 * 을 이용해 두 행렬을 곱할 때, 원소의 곱으로 적용이 되지 행렬의 곱을 의미하는 것이 아니다.
numpy의 덧셈과 동일하게 1 0 1 을 복제해 원소끼리 곱한다.
a * b
array([[1, 0, 3],
[4, 0, 6],
[7, 0, 9]])
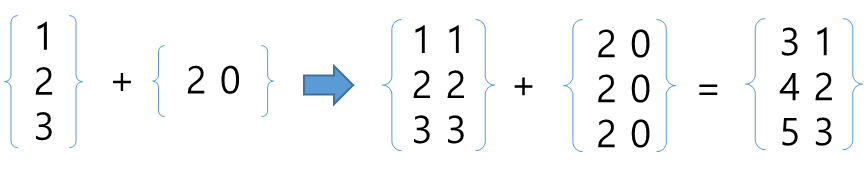
3. M x 1 1 x N 연산
서로 보완하듯이 복제되어 연산한다.
연산 결과 M x N 행렬이 생성된다.
즉 복제되어 M x N + M x N 으로 연산 된다.
c = np.array([1, 2, 3])
d = np.array([2, 0])
c = c[ : , None] # 행벡터를 열벡터로 바꾸기
c + d
array([[3, 1],
[4, 2],
[5, 3]])