방통대 과제 30점(만점) 맞은 기념으로 올리는 글입니다.

다음은 거래된 집값에 대한 자료의 일부이다. 독립변수( X2 , X3 , X4 ) 를 이용하여 집값 Y를 추정하고자 한다. 회귀모형식을 적합하고 결과를 설명하시오.

데이터 불러오기

X1 transaction date 거래일
X2 house age 집년식
X3 distance to the nearest MRT station 가까운 대중교통 역까지의 거리
X4 number of convenience stores 편의점 수
X5 latitude 위도
X6 longitude 경도
Y house price of unit area 집값

회귀모형 적합하기

회귀방정식

추정된 회귀방정식은 Y = 42.977286 - 0.252856 X2 -0.005379 X3 + 1.297443 * X4 입니다.

해석하기

이 모형에 대한 결정계수 R2 = 0.5411로서 중회귀모형이 종속변수 Y의 총변동을 약 54.11% 정도 설명하고 있음을 나타냅니다. 또한 추정값의 표준오차 √MSE = 9.251으로서 잔차의 표준편차(시그마, σ )의 추정값이 9.251입니다.
X2의 t0값 = -0.252856 / 0.040105 = -6.305 로서, 유의확률 p값 = 7.47e-10
이다. 유의수준 a = 0.05에서 귀무가설을 기각한다. 즉, X2인 house age는 Y인 house price of unit area를 설명하는 데 큰 영향을 미친다고 볼 수 있습니다.

추가변수그림 그리기

avPlots(house_lm)

추가변수그림에서는 X2와 X4가 다소 강한 선형성이 보여지며, X3은 보여지지 않습니다. X3에 비해, X2와 X4가 회귀모형에 매우 유의한 변수로 추정됩니다.

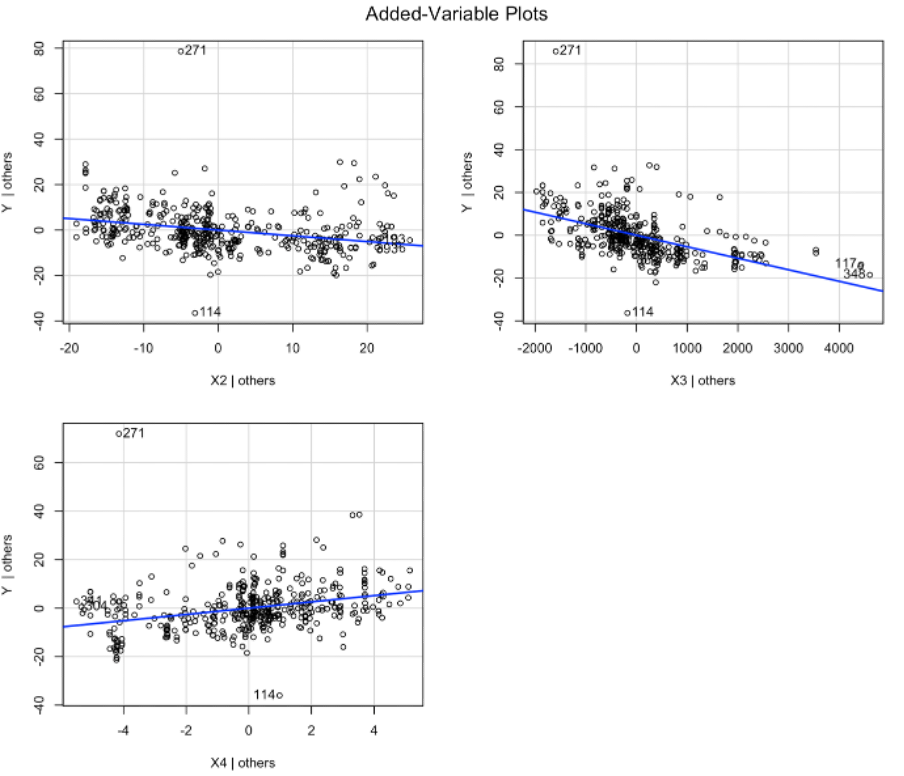
ANOVA 분산분석표

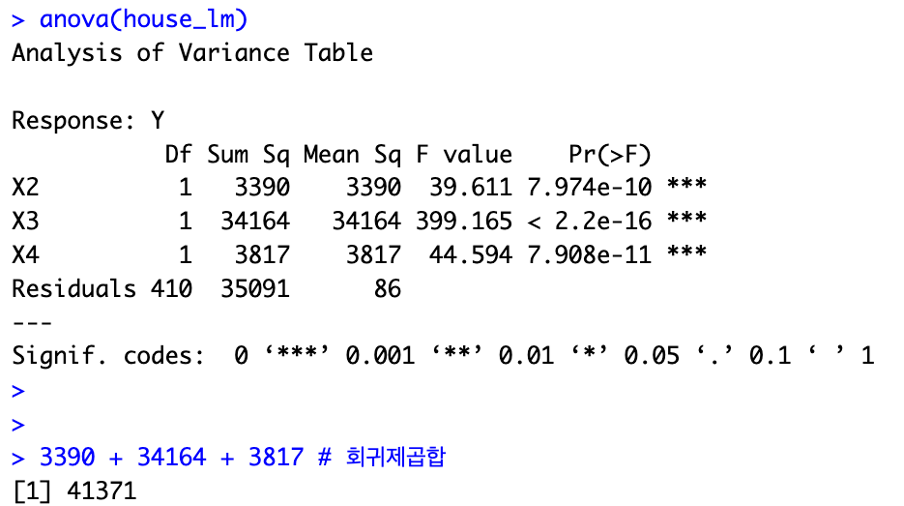
회귀제곱합은 41371
F값은 161.1
p값 2.2e-16 으로서, 매우 작아 중회귀모형이 매우 유의미함을 알 수 있습니다.

또한 오차분산 σ2 의 추정값 MSE = 86 임을 알 수 있습니다.