Python 알고리즘 _이분검색&합병정렬

📍 이분검색(Binary Research)

정렬된 리스트에서 주어진 키 존재

• 분할정복
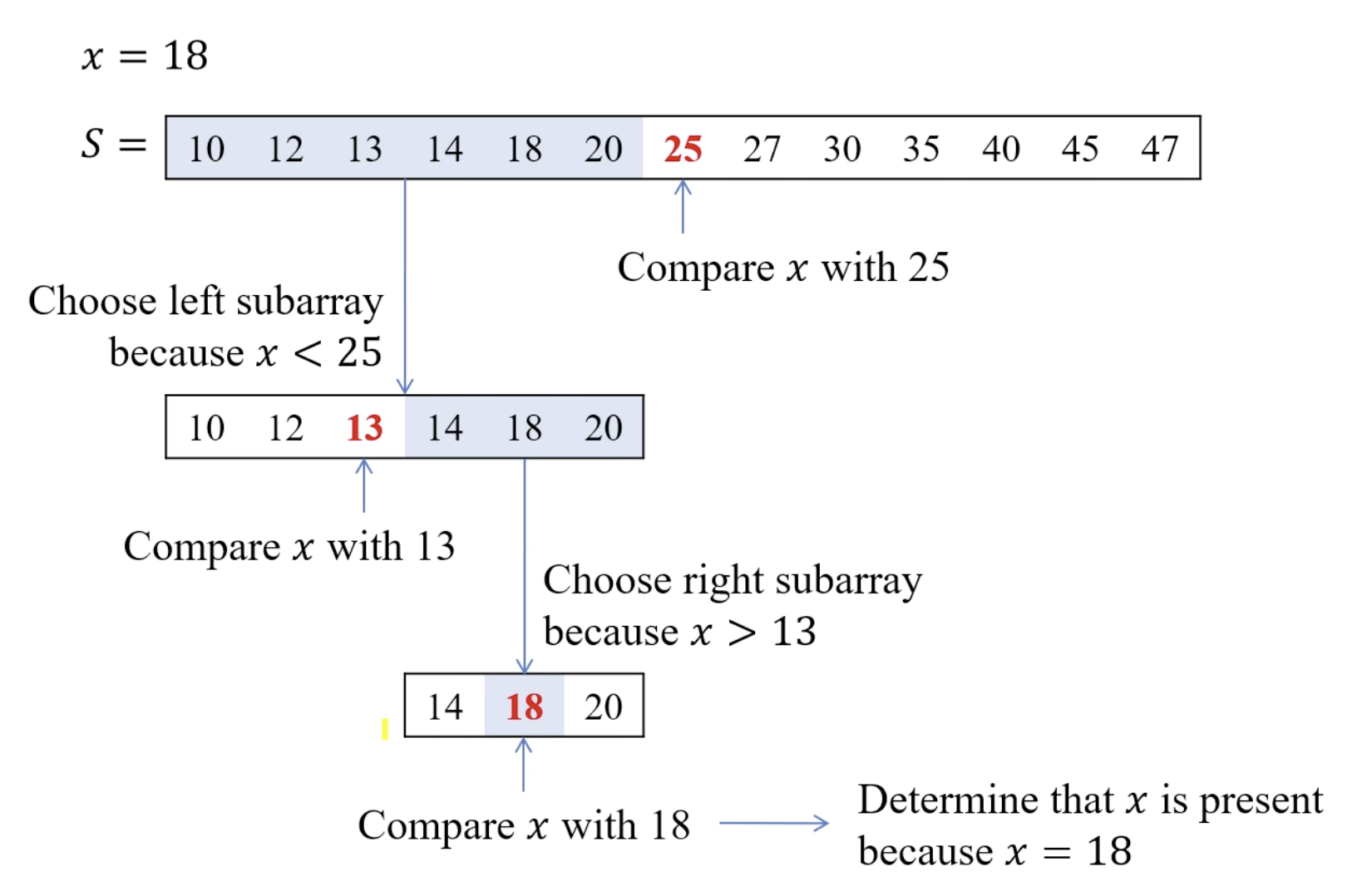
  Q. 정렬된 리스트 S에 어떤 키 x가 존재하는가? : 존재하면 x의 위치, 아니면 -1 리턴

💡 방법
1. [Divide] S의 가운데 원소와 x를 비교하여 같으면 리턴, 아니면 두개로 분할
2. [Conquer] x가 정가운데 보다 크면 오른쪽, 작으면 왼쪽을 재귀호출
3. [Obtain] 리스트에서 얻은 답을 리턴

코드 분석 : Binary Research (Recursive)

# 이분검색
def location(S, low, high):
    if(low > high):
        return 0
    else:
        mid = (low + high) // 2  # 리스트의 가운데 값 출력
        if(x == S[mid]):  # 만약 선택한 숫자가 가운데 있으면 그대로 리턴
            return mid
        elif (x < S[mid]):  # 선택한 수가 가운데 수 보다 작으면 왼쪽 탐색
            return location(S, low, mid - 1)
        else:   # 선택한 수가 가운데 수 보다 크면 오른쪽 탐색
            return location(S, mid + 1, high)

#출력
  S = [-1, 10, 12, 13, 14, 18, 20, 25, 27, 30, 35, 40, 45]
  x = 18
  loc = location(S, 1, len(S)-1) # 리스트, 1번(가장 작은 탐색수), n번(리스트의 수)
  print('S = ',S)
  print('x = ', x)
  print('loc = ', loc)

#결과
S =  [-1, 10, 12, 13, 14, 18, 20, 25, 27, 30, 35, 40, 45]
x =  18
loc =  5

📍 합병정렬(Merge Sort)

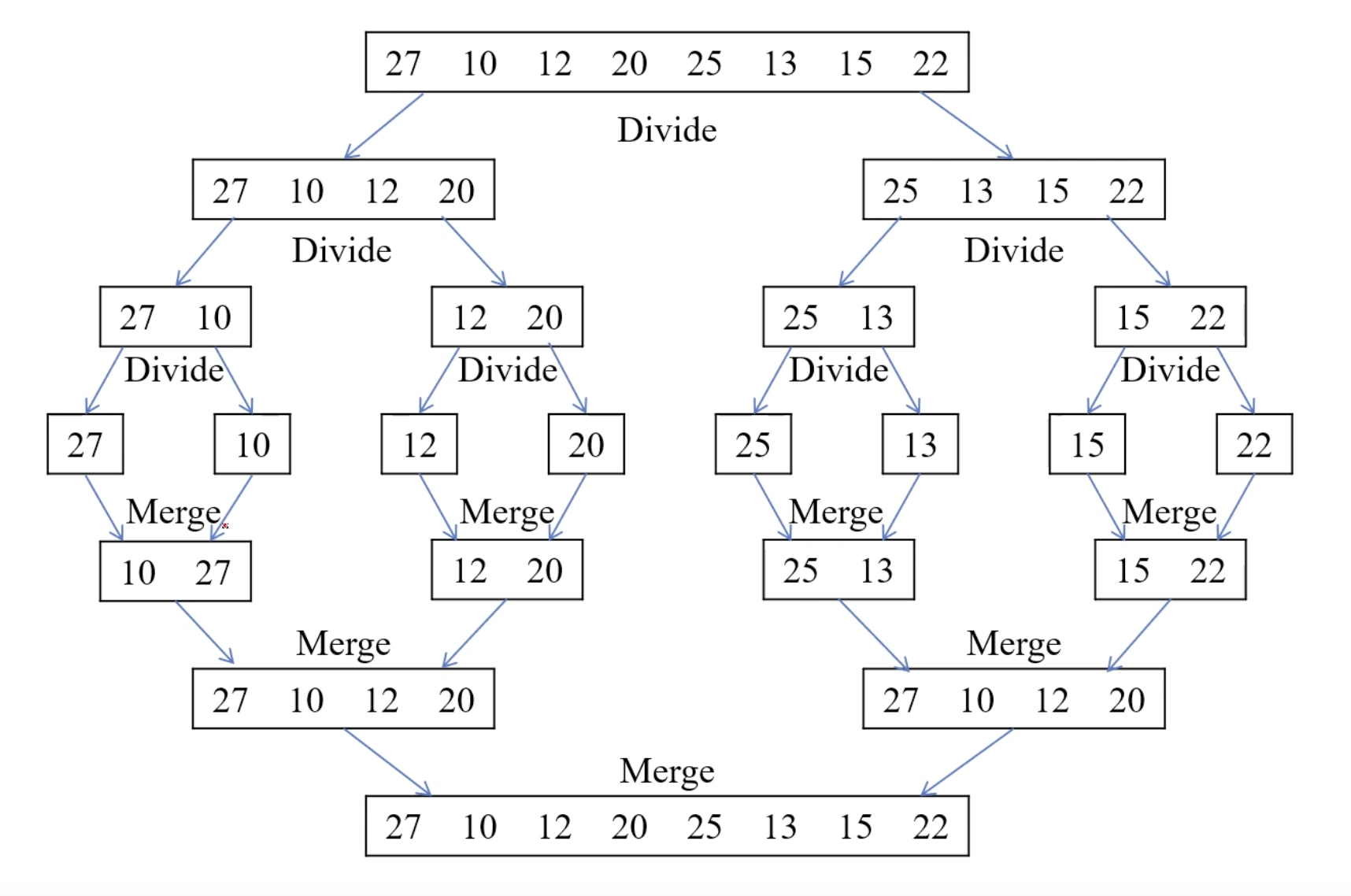
분할정복에 해당된다

💡 방법
1. [Divide] 원소가 n개인 리스트 S를 n/2개의 원소를 가진 두개의 리스트로 분할
2. [Conquer] 왼쪽/오른쪽 두개 리스트를 각각 재귀적으로 합병정렬
3. [Combine] 두개의 정렬된 리스트를 하나로 합병하여 리턴

✏️ 코드 분석

#합병정렬
def mergesort(S):
    n = len(S)
    if(n <= 1):  # 원소 개수가 하나면 그대로 출력
        return S
    else:
        mid = n // 2  # 리스트 두개로 분할
        U = mergesort(S[0:mid])  # 왼쪽 정렬
        V = mergesort(S[mid:n])  # 오른쪽 정렬
        return merge(U,V)   #합병하기
        
#merge 함수작성
def merge(U,V):  # 합병함수
    S = [] 
    i = j = 0
    while (i < len(U) and j < len(V)): 
        if(U[i] < V[j]):  # 각각의 정렬된 리스트 원소를 비교해서 작은쪽을 먼저 더하기
            S.append(U[i])
            i+=1
        else:
            S.append(V[j])
            j+=1
    if(i < len(U)):  # 한쪽의 모든 원소 배치가 끝나면 남은 원소를 그대로 더하기
        S += U[i : len(U)]
    else:
        S += V[j: len(V)]
    return S

#출력
  S = [27, 10, 12, 20, 25, 13, 15, 22]
  print('Before: ' ,S)
  X = mergesort(S)
  print('After : ', X)
  
# 결과
U =  [27] V =  [10]
U =  [12] V =  [20]
U =  [10, 27] V =  [12, 20]
U =  [25] V =  [13]
U =  [15] V =  [22]
U =  [13, 25] V =  [15, 22]
U =  [10, 12, 20, 27] V =  [13, 15, 22, 25]

Before:  [27, 10, 12, 20, 25, 13, 15, 22]
After :  [10, 12, 13, 15, 20, 22, 25, 27]

❗️ 합병 정렬의 문제점 ❗️
입력 리스트 S 이외에 U,V를 추가적으로 사용 => 메모리 사용이 비효율적
mergesort() 호출마다 U, V 새로 생성함 / 첫번째 호출 n개, 두번째 n/2 .. 전체 호출 : 2n

✏️ 수정된 코드

def merge2(S, low, mid, high):
    U = []
    i = low
    j = mid + 1
    while (i <= mid and j <= high):
        if (S[i] < S[j]):
            U.append(S[i])
            i += 1
        else:
            U.append(S[j])
            j += 1
    if (i <= mid):
        U += S[i : mid + 1]
    else:
        U += S[j : high + 1]
    for k in range(low, high + 1):
        S[k] = U[k - low]

def mergesort2(S, low, high):  
    if(low < high):
        mid = (low + high) // 2
        mergesort2(S, low, mid)  # S에서 자체적으로 정렬해서 리턴
        mergesort2(S, mid+1, high)
        merge2(S, low, mid, high)

=> 시간복잡도를 n으로 줄일 수 있다!!