알고리즘의 성능측정

🔎 알고리즘 성능분석

시간복잡도 : 입력된 N의 크기에 따라 실행되는 조작의 수를 나타낸다.
공간복잡도 : 알고리즘이 실행될때 사용하는 메모리의 양을 나타낸다.

퍼포먼스 측정 : 실행시간, 명령의 숫자세기 (컴퓨터 성능 / 프로그래밍 언어에 따라 다름)
복잡도 분석 : 입력 크기(n)에 따른 단위연산의 실행횟수 세기

입력크기(f(n)) : 가장 안쪽 for루프 안에 있는 곱셈/나눗셈, 조건문안의 식
단위연산 : 비교연산

• 순차탐색
  최악의 경우 모두 비교 : W(n) = n
  최적의 경우 한번 비교 : B(n) = 1
  평균의 경우 (주어진 키 x가 k번째 있으면 k번 비교) : A(n) = (n+1)/2

def search_list(a, x):
    n = len(a)   # 입력 크기 n
    result = []  # 새 리스트를 만들어 결괏값을 저장
    for i in range(0, n):     # 리스트 a의 모든 값을 차례로
        if x = = a[i]:        # x 값과 비교하여
            result.append(i)  # 같으면 위치 번호를 결과 리스트에 추가

    return result # 만들어진 결과 리스트를 돌려줌

📍 어떤 알고리즘이(궁극적으로) 더 빠른가?

시간 복잡도 : 입력크이 n에 대한 단위연산 횟수의 함수 f(n)
ex) f(n) = n 과 n^2 => n이 처음엔 느려보이나 숫자가 높아지면 n이 더 빠름
차수(order) : 알고리즘의 궁극적인 성능 분류
=> 모든 1차시간 알고리즘은 2차시간 알고리즘 보다 궁극적으로 빠르다!!

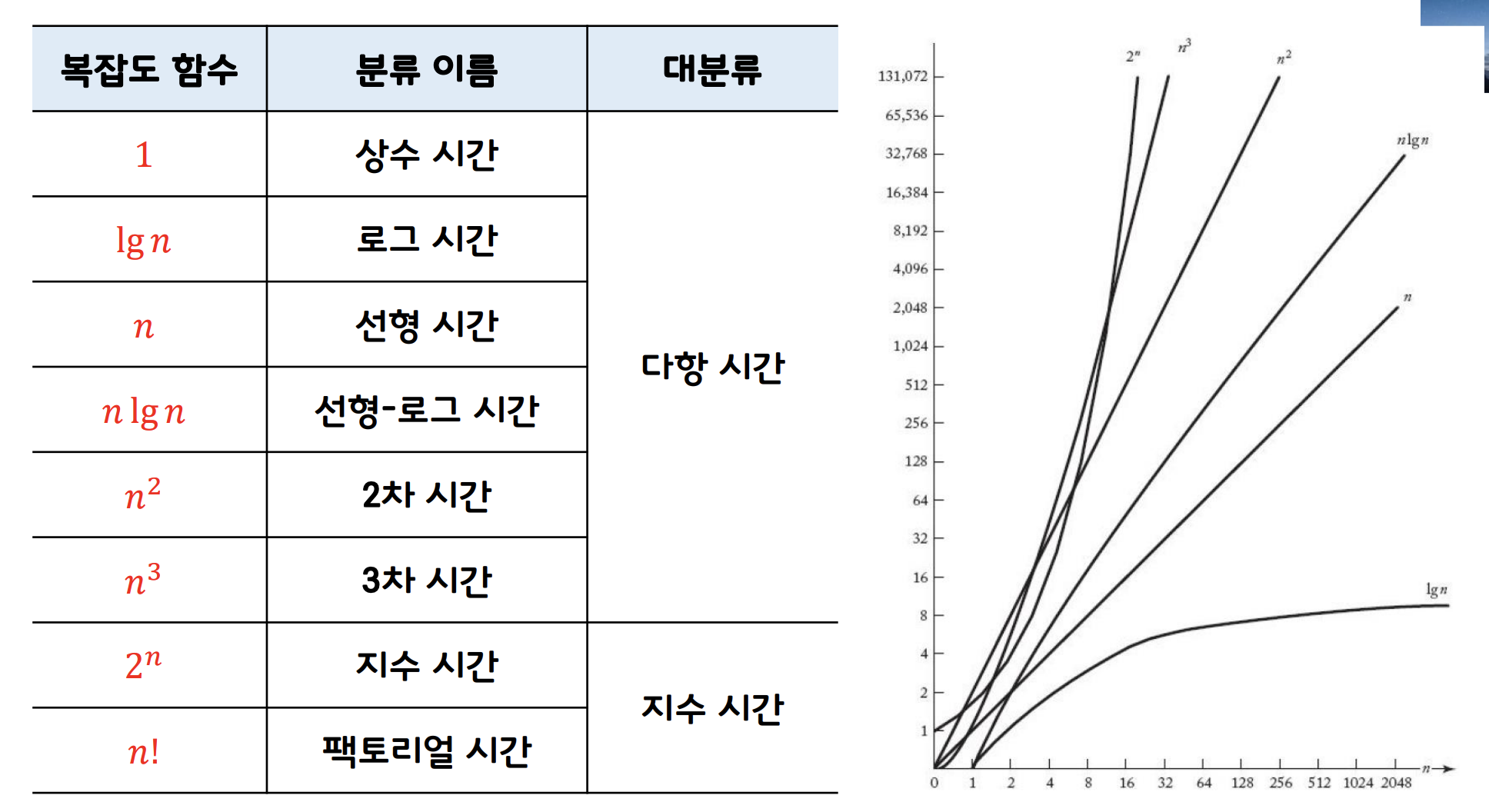
💡 시간 복잡도의 차수로 성능을 분류할수 있다.

= 낮은 차수를 버리고 가장 높은 차수를 비교한다.
점근적 표기법으로 알고리즘의 실행시간 성장률을 표기한다.

• 점근적 표기법 (빅오, 오메가, 세타)
  빅오(O) : 점근적 상한을 표기 (이거보다 더 커지지 않음!)
  오메가(Ω) : 점근적 하한을 표기
  세타(θ) : 상한/하한 둘다 동시에 만족