CS224N (2) Word Vectors and Word Senses

Sanghyeok Choi·2021년 7월 4일

NLP cs224n

CS224N

목록 보기

2/3

Thumbnail image

Word2vec

Review

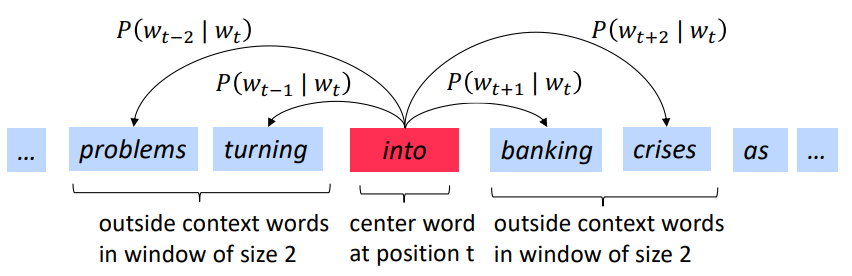
Iterate through each word of the whole corpus
Predict surrounding words using word vectors
Calculate $J(\theta)$ and $\nabla_{\theta}{J(\theta)}$
Update $\theta$ so you can predict well
Each row of $U\in \Reals^{V\times d}$ is a word vector!
Note: You can use $V$ or $mean(U, V)$ instead of $U$ , or use $V$ for centre words and $U$ for context words if it is possible.

Q. How to avoid too much weight on the high frquency words(like 'the', 'of', 'and')?
A. Discard the first biggest component of word vector! It contains information of frequency.

Stochastic Gradient Descent

Problem: $\nabla_{\theta}{J(\theta)}$ is very expensive to compute
Stochastic Gradient Descent(SGD): Repeatedly sample windows, and update after each one!

While True:
    window = sample_window(corpus)
    theta_grad = evaluate_gradient(J, window, theta)
    theta = theta - alpha * theta_grad

Negative Sampling

Problem:
$P(o\mid c)= \frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}$ ... normalization factor (demoninator) is too computationally expensive.
Negative Sampling: Calculate the probability above with randomly selected negative(noise) pairs.
$J_{neg-sample}(\bm{o}, \bm{v}_c, \bm{U})=-\log(\sigma(\bm{u}_o^T\bm{v}_c))-\sum\limits_{k=1}^{K}\log(\sigma(-\bm{u}_k^T\bm{v}_c))$
- $\bm{u}_o$ is real outside words
- $\bm{u}_k$ is random neg-samples
- $K$ is number of neg-samples (10-20 would be fine)
- Maximize probability that real outside word appears.
  Minimize probability that random words appear around centre word.
$P(w)=U(w)^{3/4}/Z$
- $P(w)$ : Sampling Probability (distribution)
- $U(w)$ : unigram distribution
- 3/4 power ⇒ common word ↓, rare word ↑ (This number determined heuristically)

GloVe

Word-document co-occurrence matrix

Word-document co-occurrence matrix will give general topics leading to "Latent Semantic Analysis"
Example of simple co-occurrence matrix:
I like deep learning.
I like NLP.
I enjoy flying.
counts I like enjoy deep learning NLP flying .
I 0 2 1 0 0 0 0 0
like 2 0 0 1 0 1 0 0
enjoy 1 0 0 0 0 0 1 0
deep 0 1 0 0 1 0 0 0
learning 0 0 0 1 0 0 0 1
NLP 0 1 0 0 0 0 0 1
flying 0 0 1 0 0 0 0 1
. 0 0 0 0 1 1 1 0
Problems with simple co-occurrence vectors:
1) Increase in size with vocabulary
2) Very high dimensional, requires a lot of storage
3) Sparsity issues with vectors
⇒ Naive solution: Singular Vector Decomposition (SVD)
⇒ Better solution: GloVe

counts	I	like	enjoy	deep	learning	NLP	flying	.
I	0	2	1	0	0	0	0	0
like	2	0	0	1	0	1	0	0
enjoy	1	0	0	0	0	0	1	0
deep	0	1	0	0	1	0	0	0
learning	0	0	0	1	0	0	0	1
NLP	0	1	0	0	0	0	0	1
flying	0	0	1	0	0	0	0	1
.	0	0	0	0	1	1	1	0

Count-based vs Direct-prediction

The methods of word representation can be categorized as "Count-based" or "Direct-prediction"

Count-based	Direct-prediction
- LSA, HAL - COALS, Hellinger-PCA	- Word2vec (Skip-gram, CBOW) - NNLM, HLBL, RNN
Advantages: - Fast training - Efficient usage of statistics	Advantages: - Generate improved performance on other tasks - Can capture complex patterns beyond word similarity
Disadvantages: - Primarily used to capture word similarity - Disproportionate importance given to large counts	Disadvantages: - Scales with corpus size - Inefficient usage of statistics

In other words, count-based methods can capture characteristics of the document because these methods receive whole corpus as an input, while the direct-prediction methods outperform in representing the syntactic and symantic features of a word.

Glove

Glove is designed to combine the advantages of both count-based and direct-prediction.
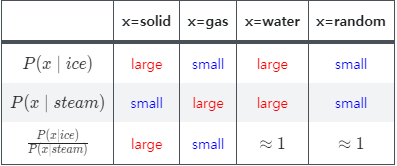
Insight: Ratio of co-occurrence probabilities can encode meaning components.

	x=solid	x=gas	x=water	x=random
$P(x\mid ice)$	large	small	large	small
$P(x\mid steam)$	small	large	large	small
$\frac{P(x\mid ice)}{P(x\mid steam)}$	large	small	$\approx1$	$\approx1$

"Ratio" makes both-related words (water) or un-related words (fashion) to be close to 1.

Q. How can we capture ratios of co-occurrence probabilities as linear meaning components in a word vector space?
A. Log-bilinear model!

Log-bilinear Model ... (What is bilinear?)
1. co-occurrence prob. $P_{ij}=P(j\mid i)=\frac{X_{ij}}{X_i}$
2. ratio of co-occurrence prob. $\frac{P_{ik}}{P_{jk}}=F(w_{i}, w_{j}, {w_k})$
  - $F$ is some mapping
3. We want $F$ to represent the information present in $P_{ik}/P_{jk}$ .
  Thus, $F(w_i, w_j, w_k) = F(w_i-w_j,w_k) = \frac{P_{ik}}{P_{jk}}$
  - Consider this: when $w_i \approx w_j$ , we want $P_{ik}/P_{jk}$ to be determined solely by word $k$ .
4. As $P_{ik}/P_{jk}$ is a scalar, $F(w_i-w_j, w_k)$ should also be a scalar.
  Thus, $F(w_i-w_j, w_k)=F((w_i-w_j)^Tw_k)= \frac{P_{ik}}{P_{jk}}$
  - While F could be taken to be a complicated function parameterized by, e.g., a neural network, doing so would obfuscate the linear structure we are trying to capture.
5. The distinction between a word and a context word is arbitrary and we are free to exchange the two roles.
  Thus, $F((w_i-w_j)^Tw_k)=\frac{F(w_i^Tw_k)}{F(w_j^Tw_k)}=\frac{P_{ik}}{P_{jk}}$
  which means, $F(w_i^Tw_k)=P_{ik}=\frac{X_{ik}}{X_i}$ and $F(w_j^Tw_k)=P_{jk}=\frac{X_{jk}}{X_j}$
6. We require that $F$ be a homomorphism between the groups $(R,+)$ and $(R>0, \times)$ .
  This simply means that we want: $F(a+b)=F(a)+F(b)$
  Thus, $F = \exp$ , and $F(w_i \cdot w_j)=\exp(w_i \cdot w_j)=P_{ij}$
7. Finally we get log-bilinear model:
  $w_i \cdot w_j = \log{P(i \mid j)}=P_{ij}$
  And from this, we also get:
  $w_x \cdot (w_a - w_b)=\log{\frac{P(x \mid a)}{P(x \mid b)}}$
Cost Function of GloVe
$J=\sum\limits_{i,j=1}^{V}f(X_{ij})(w_i^T\tilde{w}_j+b_i+\tilde{b}_j-\log{X_{ij}})$
- $f$ is some special function that is designed to capping the effect of very common words.
- Note: $b_i$ and $b_j$ is introduced to obtain symmetricity between word $i$ and $j$
- For more details, check the original GloVe paper.
vs Word2vec
Someone's opinion: stackoverflow