CS224N (3) Word Window Classification, Neural Networks, and Matrix Calculus

Softmax and Cross-entropy

• Softmax: $p(y \mid x)=\cfrac{\exp(W_{y\cdot}x)}{\sum^C_{c=1}{\exp(W_{c\cdot}x)}}$
  • $W_{y\cdot}$ is $y^{th}$ row of some weight matrix $W$
• Cross-entropy: $H(p, q)=-\sum\limits^{C}_{c=1}{p(c)\log{q(c)}}$
  • True probability: $p$
  • Modeled probability: $q$
• Cross-entropy loss function over dataset $\{x_i,y_i\}^N_{i=1}$:
  $J(\theta)=-\cfrac{1}{N}\sum\limits^{N}_{i=1}{\log{\left(\cfrac{\exp(W_{y_i\cdot}x_i)}{\sum^C_{c=1}{\exp(W_{c\cdot}x_i)}}\right)}}$ ... where $\theta = \left[ W_{\cdot 1} \dots W_{\cdot d}\right] \in \Reals^{C \times d}$
  • For classification, we want to minimize $J(\theta)$, which means we want to maximize probability of correct class $y$ => update $\theta := \theta -\alpha\nabla_{\theta}{J(\theta)}$
  • cf) Binary cross-entropy loss: $J(\theta)=-\frac{1}{N}\sum\limits^{N}_{i=1}(y_i\log\hat{y_i}+(1-y_i)\log(1-\hat{y_i}))$

---

Neural Networks

• Softmax alone is not very powerful. It only gives linear decision boundaries.
• Neural networks can learn much more complex functions and nonlinear decision boundaries.

Artificial Neuron and Neural Network

Neuron	Neural Network
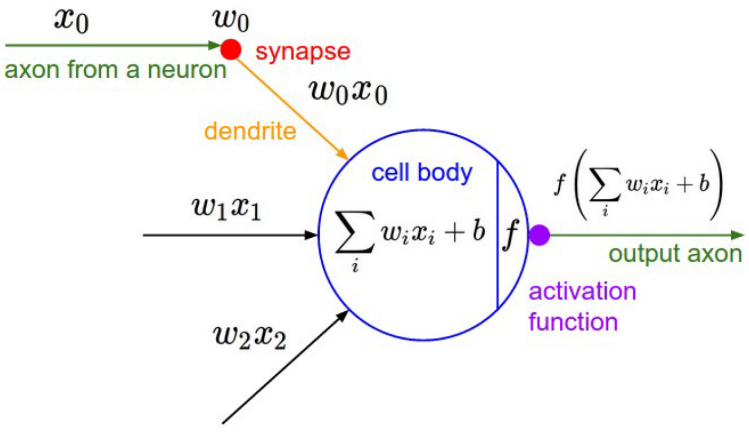Image from: here	Image from: here

• A neuron can be a binary logistic regression unit
• $f =$ nonlinear activation function (e.g. sigmoid)
• A neural network = running several logistic regressions at the same time
  And feed the outputs of a layer into next layer of neurons
• In matrix notation,
  $z=Wx+b$ ... ($x$ is an input vector of a layer)
  $a=f(z)$ ... ($a$ is output vector from the layer, and it will be fed into next layer)

---

Window Classification

• In general, classifying single words is rarely done because meaning of a word depends on context
  • "To sanction" can mean "to permit" or "to punish"
  • "Paris" can mean "Paris, France" or "Paris Hilton"
• Window Classification: classify a word in its context window of neighboring words
  • To classify a center word, take concatenation of word vectors surrounding it in a window.
  • Example: Classify "Paris" in the context with window length 2: Image from: here
  • $x_{window}\in\Reals^{5d}$ is now an input vector of a neural net
• Neural Network Feed-forward Computation
  • Let's assume a NER location classification task (classify whether the center word is a Location or not)
  • $s$ = score("museums in Paris are amazing")
  • $s = U^Tf(Wx+b)$
  • $x\in\Reals^{5d\times1}, W\in\Reals^{n\times5d}, U\in\Reals^{n\times1}$ Image from: here
  • The middle layer learns non-linear interactions between the input word vectors
• The max-margin loss
  • $s=$ True window's score
  • $s_c=$ Corrupt window's score
  • $J = \max(0, 1-s+s_c)$ ... minimizing $J$ makes $s$ larger and $s_c$ lower
  • This is not differentiable but it is continuous -> we can use SGD by computing $\nabla_{\theta}J(\theta)$

Matrix Calculus

Gradients

• Given a function $f$ with 1 output and n inputs

  • $f(\bm{x}) = f(x_1, x_2, ..., x_n)$
  • Gradient: $\nabla_x{f} = \cfrac{\partial f}{\partial \bm{x}}=\left[ \cfrac{\partial f}{\partial x_1}, \cfrac{\partial f}{\partial x_2}, ..., \cfrac{\partial f}{\partial x_n} \right]$

• Given a function $f$ with m outputs and n inputs

  • $\bm{f(x)}=\lbrack f_1(x_1,...,x_n), ..., f_m(x_1,...,x_n) \rbrack$
    
    
  • Jacobian: $\cfrac{\partial \bm{f}}{\partial \bm{x}}=\begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \dots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \dots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}$, i.e. $\left( \cfrac{\partial \bm{f}}{\partial \bm{x}} \right)_{ij}=\cfrac{\partial f_i}{\partial x_j}$

• Example: Elementwise activation function

  • $\bm{h} = f(\bm{z})$, where $\bm{h},\bm{z} \in \Reals^n$
  • Jacobian: $\cfrac{\partial \bm{h}}{\partial \bm{z}}= \begin{bmatrix}f'(z_1) & & \text{\huge0} \\ \\ & \ddots & \\ \text{\huge0} & & f'(z_n)\end{bmatrix} =\mathrm{diag}(f'(\bm{z})){}{}$

Apply to NER location neural net

• $s = U^Tf(Wx+b)$

  • Break up the equation into simple pieces
    • $\bm{x} \in \Reals^n$ is input
    • $\bm{z}=\bm{Wx}+\bm{b}$, where $\bm{z}, \bm{b} \in \Reals^m$, $\bm{W} \in \Reals^{m \times n}$
    • $\bm{h}=f(\bm{z})$, where $f$ is elementwise activation function, $\bm{h} \in \Reals^m$
    • $s=\bm{u}^T\bm{h}$, where $\bm{u} \in \Reals^m$
      
      

• Partial derivatives of score $s$
  

  • $\cfrac{\partial s}{\partial \bm{b}}$
    
    $=\cfrac{\partial s}{\partial \bm{h}}\cfrac{\partial \bm{h}}{\partial \bm{z}}\cfrac{\partial z}{\partial \bm{b}}$ ... by chain rule
    
    $=\bm{u}\cdot \begin{bmatrix}f'(z_1) & & \text{\huge0} \\ \\ & \ddots & \\ \text{\huge0} & & f'(z_n)\end{bmatrix} \cdot \bm{I}$
    
    $=\bm{u}^T\mathrm{diag}(f'(\bm{z}))\bm{I}$
    $=\bm{u}\circ f'(\bm{z})$ ... "$\circ$" is elementwise multiplication
    
    
  • $\cfrac{\partial s}{\partial \bm{W}}$ ... should be $m \times n$ matrix
    
    $=\cfrac{\partial s}{\partial \bm{h}}\cfrac{\partial \bm{h}}{\partial \bm{z}}\cfrac{\partial \bm{z}}{\partial \bm{W}}$
    
    $=(\bm{u}\circ f'(\bm{z}))\bm{x}^T$ ... $(m \times 1)(1 \times n) \to (m \times n)$
    Here we used the result already computed above $\left( \cfrac{\partial s}{\partial \bm{h}}\cfrac{\partial \bm{h}}{\partial \bm{z}} = \bm{u}^T\circ f'(\bm{z}) \in \Reals^m\right)$

• Update weights

  • $\bm{b} = \bm{b} - \alpha\cfrac{\partial s}{\partial \bm{b}}$
  • $\bm{W} = \bm{W} - \alpha\cfrac{\partial s}{\partial \bm{W}}$

---

If there is something wrong in my writing or understanding, please comment and make corrections!

---

[references]
1. https://youtu.be/8CWyBNX6eDo
2. https://web.stanford.edu/class/archive/cs/cs224n/cs224n.1194/slides/cs224n-2019-lecture03-neuralnets.pdf
3. https://en.wikipedia.org/wiki/Partial_derivative