[백준 18290] NM과 K -Java

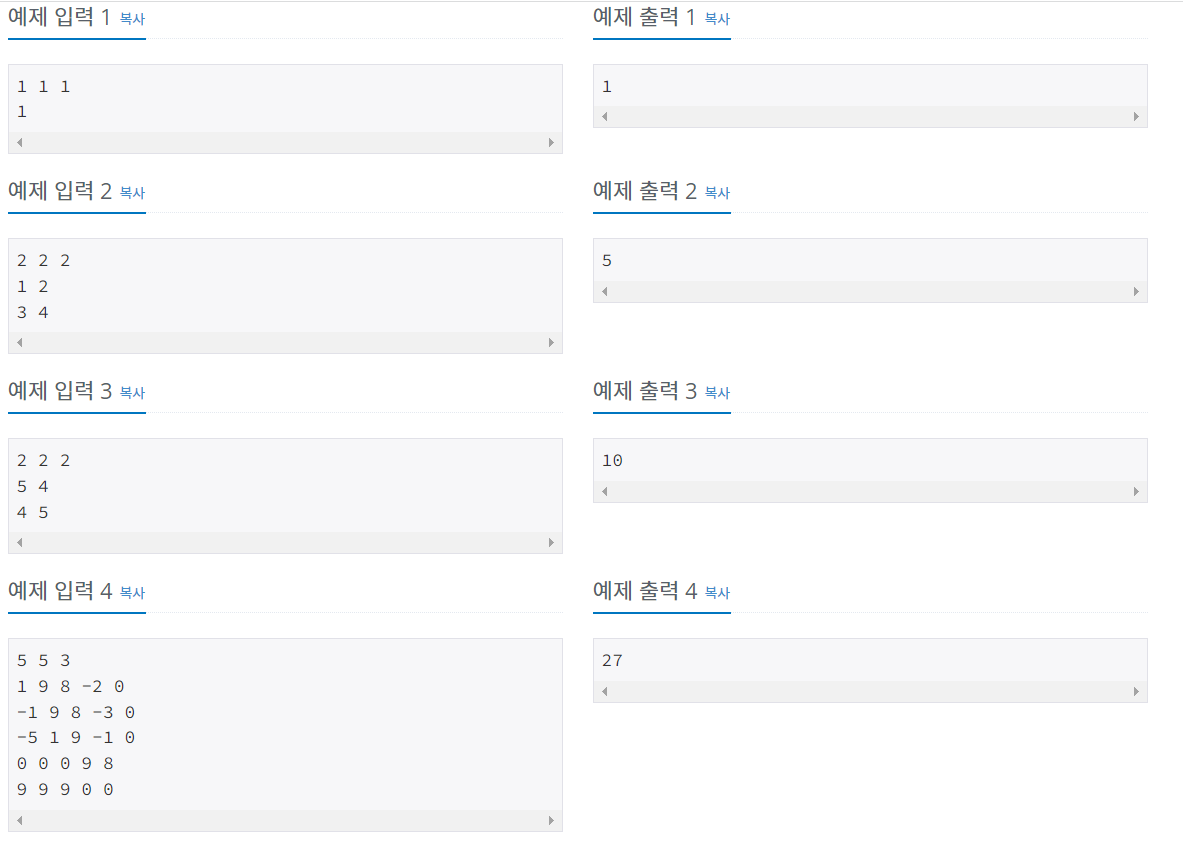
문제)
크기가 N×M인 격자판의 각 칸에 정수가 하나씩 들어있다. 이 격자판에서 칸 K개를 선택할 것이고, 선택한 칸에 들어있는 수를 모두 더한 값의 최댓값을 구하려고 한다. 단, 선택한 두 칸이 인접하면 안된다. r행 c열에 있는 칸을 (r, c)라고 했을 때, (r-1, c), (r+1, c), (r, c-1), (r, c+1)에 있는 칸이 인접한 칸이다.

입력)
첫째 줄에 N, M, K가 주어진다. 둘째 줄부터 N개의 줄에 격자판에 들어있는 수가 주어진다.

출력)
선택한 칸에 들어있는 수를 모두 더한 값의 최댓값을 출력한다.

해당 문제는 인접하지 않는 숫자 중, k개의 숫자를 뽑아 합이 제일 큰 것을 찾는 문제이다

모든 경우의 수를 찾아야 해서, 완전탐색 문제이며 DFS를 이용해야 겠다고 생각했다. 하지만 실수가 있었는데, 문제에서 인접하지 않는 수를 찾으려면 대각선에 위치한 숫자를 더해주면 되지 않을까 라는 생각이였다.
운이 좋게도 예제문제들은 다 통과하여 정답제출을 했지만 역시나 틀렸다.

이 문제의 푸는 방법은 상,하,좌,우 인접한 숫자인지 를 판단하여 인접할 경우에는 다음 숫자로 넘어가고 인접하지 않는 숫자는 더해주는 방법을 이용해야한다.

해당 구현한 코드는 아래와 같다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Iterator;
import java.util.StringTokenizer;

public class Main {

	static int N, M, K, answer = Integer.MIN_VALUE;
	static int[][] map;
	static boolean[][] visited;
	static int[] dr = { -1, 1, 0, 0 };
	static int[] dc = { 0, 0, -1, 1 };

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());

		N = Integer.parseInt(st.nextToken());
		M = Integer.parseInt(st.nextToken());
		K = Integer.parseInt(st.nextToken());
		map = new int[N][M];
		visited = new boolean[N][M];

		for (int i = 0; i < N; i++) {
			st = new StringTokenizer(br.readLine());
			for (int j = 0; j < M; j++) {
            	// 격자판
				map[i][j] = Integer.parseInt(st.nextToken());
			}
		}

		// 탐색 시작
		search(0, 0, 0, 0);
		System.out.println(answer);
	}

	private static void search(int cnt, int preR, int preC, int sum) {
    	// 숫자가 K개만큼 채워졌을시 값 리턴
		if (cnt == K) {
			answer = Math.max(answer, sum);
			return;
		}

		boolean notAdj;
        // preR : 시작 인덱스를 자신의 위치에서 시작
		for (int i = preR; i < N; i++) {
			for (int j = (preR == i ? preC : 0); j < M; j++) {
            	// 자기자신이 이미 true일 경우 다음으로 이동
				if (visited[i][j]) {
					continue;
				}

				notAdj = true;
                // 상, 하, 좌, 우 인접한 숫자인지 체크
				for (int dir = 0; dir < 4; dir++) {
					int nr = i + dr[dir];
					int nc = j + dc[dir];

					if ((nr >= 0 && nr < N && nc >= 0 && nc < M) && (visited[nr][nc])) {
                    	//인접한 숫자가 존재할시 다음으로 넘어감 
						notAdj = false;
						break;
					}
				}

				// notAdj = true일시 인접하지 않는 숫자이므로,
                // 해당 map[i][j] 값을 더함
				if (notAdj) {
					visited[i][j] = true;
					search(cnt + 1, i, j, sum + map[i][j]);
					visited[i][j] = false;
				}
			}
		}
	}
}