문제

https://www.acmicpc.net/problem/3687

성냥개비는 숫자를 나타내기에 아주 이상적인 도구이다. 보통 십진수를 성냥개비로 표현하는 방법은 다음과 같다.

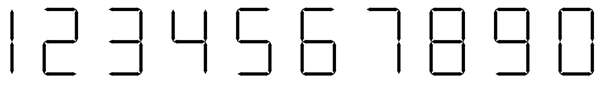
성냥개비의 개수가 주어졌을 때, 성냥개비를 모두 사용해서 만들 수 있는 가장 작은 수와 큰 수를 찾는 프로그램을 작성하시오.

---

입력

첫째 줄에 테스트 케이스의 개수가 주어진다. 테스트 케이스는 최대 100개 이다. 각 테스트 케이스는 한 줄로 이루어져 있고, 성냥개비의 개수 n이 주어진다. (2 ≤ n ≤ 100)

---

출력

각 테스트 케이스에 대해서 입력으로 주어진 성냥개비를 모두 사용해서 만들 수 있는 가장 작은 수와 가장 큰 수를 출력한다. 두 숫자는 모두 양수이어야 하고, 숫자는 0으로 시작할 수 없다.

---

풀이

접근방법

시간제한 1초, 메모리 128MB이다.
(2 ≤ n ≤ 100)

1. 테스트 케이스의 개수가 주어진다.
2. 직관적으로 특정 계산을 할 때, 이전의 결과가 사용될 것 같다.
   ( 성냥 2개를 사용해서 만들 수 있는 가장 작은 수는 1과 같은.. )

DP가 필요한 문제이다.
n의 크기가 100까지이므로 모두 계산해두고 시작하자.

공통

각 숫자를 만들 때, 몇 개의 성냥이 필요한가?

숫자			: 0 1 2 3 4 5 6 7 8 9
필요한 성냥	: 6 2 5 5 4 5 6 3 7 6

n개의 성냥으로 만들 수 있는 최솟값과 최댓값을 나열해보자.

성냥의개수	최소		최대
2			1		1
3			7		7
4			4		11
5			2		71
6			6		111
7			8		711
8			10		1111
9			18		7111
10			22		11111

- 숫자 하나를 만들 때 최소 2개의 성냥이 필요하다.
- 숫자 하나는 최대 7개로 만들어질 수 있다.

2가지를 인지해야 한다.

최소값 구하기

N=9인 경우를 생각해 보자.
최대 7개가 하나의 숫자를 이루므로, 2 자릿수가 만들어질 것이다.
그렇다면 ab를 만들기 위해 a와 b의 조합은 2+7, 3+6, 4+5, 5+4, 6+3, 7+2이 된다.
(2+7 -> a 자리에 2개, b 자리에 7개를 할당한다는 의미)

2+7 -> 18 이 만들 수 있는 가장 작은 수
3+6 -> 70
4+5 -> 42
5+4 -> 24
6+3 -> 67
7+2 -> 81

10, 11 ... 마찬가지로 한 번 생각해보자.

최대값 구하기

단순하다.

• 짝수인 경우
  1이 반복된다.
• 홀수인 경우
  n-1의 수에서 가장 앞자리가 7이다.

주의할 점

숫자			: 0 1 2 3 4 5 6 7 8 9
필요한 성냥	: 6 2 5 5 4 5 6 3 7 6

성냥 6개를 써서 만들 수 있는 가장 작은 숫자는 0이다.
하지만 숫자는 0으로 시작할 수 없다. ( 05 -> X, 50 -> O)
이로 인해 발생할 수 있는 독특한 경우가 있을까?? 문제를 풀기 전 꼭 생각해 보자.

---

코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;

public class Main {

	static int N, T;
	static long[] min;
	static String[] max;

	public static void main(String[] args) throws Exception {
		BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

		T = stoi(in.readLine());
		min = new long[101];
		max = new String[101];

		StringBuilder sb = new StringBuilder();

		calculateMin();
		calculateMax();
		for (int i = 0; i < T; ++i) {
			N = stoi(in.readLine());
			sb.append(min[N]).append(" ").append(max[N]).append("\n");
		}
		System.out.println(sb);
	}

	private static void calculateMin() {
		Arrays.fill(min, Long.MAX_VALUE);
		min[2] = 1;
		min[3] = 7;
		min[4] = 4;
		min[5] = 2;
		min[6] = 6;
		min[7] = 8;
		min[8] = 10;
		//	숫자 		: 0 1 2 3 4 5 6 7 8 9
		//	필요한 성냥	: 6 2 5 5 4 5 6 3 7 6
		int[] count = {1, 7, 4, 2, 0, 8};
		for (int i = 9; i <= 100; ++i) {
			for (int j = 2; j <= 7; ++j) {
				min[i] = Math.min((min[i-j] * 10) + count[j-2], min[i]);
			}
		}
	}

	private static void calculateMax() {
		max[2] = "1";
		max[3] = "7";
		for (int i = 4; i <= 100; ++i) {
			if (isOdd(i)) {
				max[i] = "7" + max[i - 3];
			} else {
				max[i] = max[i - 2] + "1";
			}
		}

	}

	private static boolean isOdd(int i) {
		if (i % 2 == 1)
			return true;
		return false;
	}

	private static int stoi(String s) {
		return Integer.parseInt(s);
	}
}