Heap

개요

완전 이진트리의 일종으로 주어진 값들 중, 최대 혹은 최소가 되는 값을 빠르게 찾을 수 있다.
중복된 값을 허용하며, 우선순위 큐가 Heap으로 구성되어 있다.

• Heap을 구현해서 하는경우는 흔하지 않지만, 종종 필요한 경우가 있다.
  생각보다 구현해서 쓰기 어렵지 않으니 한 번쯤 해보자. 생각보다 유용하다.

• Max Heap : 부모가 항상 자식보다 큰 경우.

• Min Heap : 부모가 항상 자식보다 작은 경우.

• 시간복잡도
  - 삽입 : O(logN)

  • 삭제 : O(logN)

설명

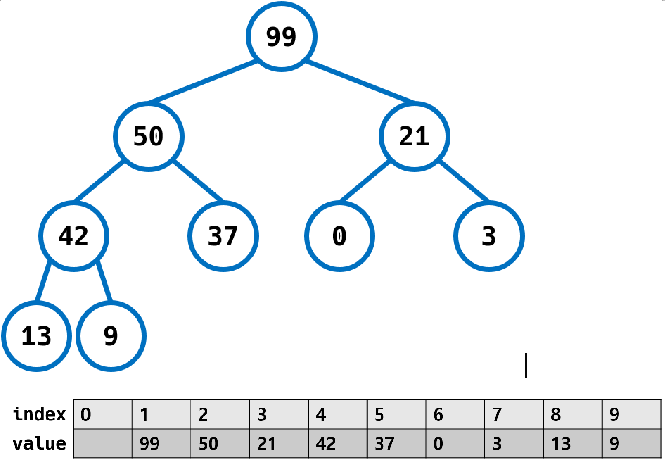
MaxHeap을 기준, 부모가 항상 자식보다 큰 경우이다.
아래 설명은 MaxHeap을 기준으로 설명되어 있다. Min Heap의 경우에는 반대로 구현하면 된다.

삽입

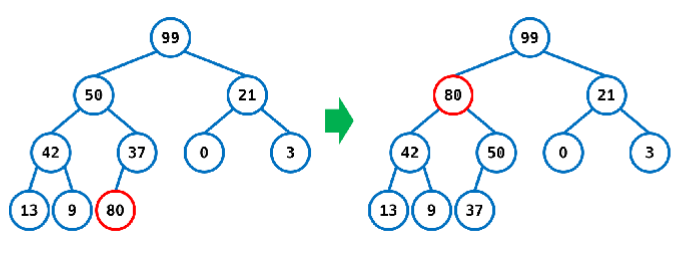
1. 배열의 가장 마지막에 데이터를 삽입한다.
2. 힙 구조를 유지하면서 부모와 값을 바꾸면서 위로 올라간다.

삭제

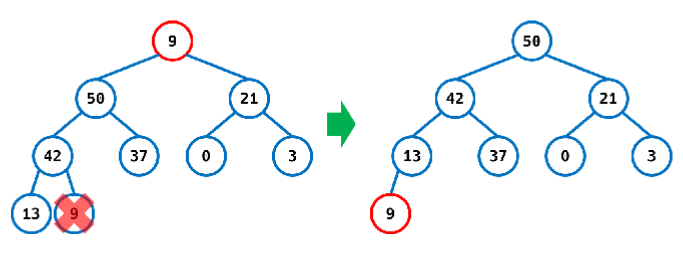
1. 배열의 가장 마지막 인덱스의 값을 가장 앞의 값으로 변경한다.
2. 배열의 Count를 1 감소시킨다.
3. 가장 앞으로 변경한 값을 Heap의 구조를 유지하면서 아래로 내린다.(1의 과정에서 작은값을 위로 올렸기 때문에 다시 자리를 찾아가야함.

#include<algorithm>
#include<iostream>
#define MAX_N 1000

int data[MAX_N + 1];
int size;

// 삽입
void push(int x) {
	int child = size;
	int parent = child / 2;
	data[++size] = x;
	for (int i = size; parent != 0 && data[parent] < data[i]; i >>= 1) {
		std::swap(data[parent], data[i]);
	}
}

// 최대값 리턴
int top(){
	if (size != 0)
		return data[1];
	// error
	return -1;
}

 // 최대값 삭제
void pop() {
	data[1] = data[size--];
	int parent = 1;
	int child = parent * 2;
	if (child + 1 <= size) {
		child = (data[child] > data[child + 1]) ? child : child + 1;
	}

	while (child <= size && data[parent] < data[child]) {
		std::swap(data[parent], data[child]);

		parent = child;
		child = child * 2;
		if (child + 1 <= size) {
			child = (data[child] > data[child + 1]) ? child : child + 1;
		}
	}
}


int main()
{
	push(50);
	std::cout << top() << std::endl;
	push(21);
	std::cout << top() << std::endl;
	push(99);
	std::cout << top() << std::endl;
	pop();
	std::cout << top() << std::endl;
	return 0;
}