서로소 집합(DisJoint Set) && Union-Find

개요

Disjoint Set, 집합론에서 공통 원소가 없는 두 집합.
서로 다른 두 개의 집합을 병합하는 Union,
집합의 원소가 어떤 집합에 속해있는지 판단하는 Find.

설명

• BFS, DFS가 아닌 Disjoint Set으로도 풀 수 있는 문제가 종종 있다.
  또한 해당 알고리즘을 알고 있다면 크루스칼 알고리즘을 매우 쉽게 구현할 수 있다.

Find

• 하나의 원소가 어떤 집합에 속해있는지를 판단
• 재귀적으로 트리를 거슬러 올라가 최상위 노드의 값을 반환.

Union : 서로 다른 두 개의 집합을 하나로 병합.

• Find 연산을 통해 최상위 노드를 비교하고 병합.

Union-Find 예시

1.Make Set

• 원소를 생성한다.
  

2.Find

• 각 원소는 병합되지 않은 서로소 집합이므로 Find(n) 호출 시 n을 반환한다.

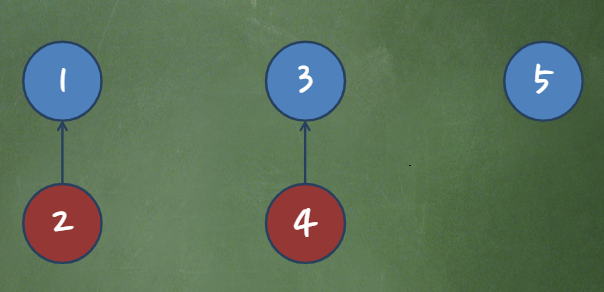
3.Union

• 1과 2를 병합, 3과4를 병합한다.
  

4.Find

각 원소에 대한 Find 함수 결과는 다음과 같다 ( Step3에서 병합)

• Find(1), Find(2) -> 1
• Find(3), Find(4) -> 3
• Find(5) -> 5
  

코드

• 어떤 언어를 사용할 지 몰라 둘 다 준비했다.

Java

public class Main {
    static int[] parent; // 최상위 값을 저장하기 위함.
    static int n = 5; // 5개라 가정

    public static void main(String[] args) {
        // Sample Test
        // Step1. MakeSet
        makeSet(n);

        // Step2. Find
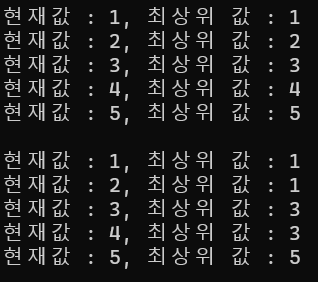
        for (int i = 1; i <= n; ++i)
            System.out.println("현재값 : " + i + ", 최상위 값 : " + parent[i]);

        // Step3. Union
        union(1, 2);
        union(3, 4);

        System.out.println();
        // Step4. Find
        for (int i = 1; i <= n; ++i)
            System.out.println("현재값 : " + i + ", 최상위 값 : " + parent[i]);
    }

    private static void union(int a, int b) {
        // 두 원소의 최상위 노드를 찾는다.
        a = find(a);
        b = find(b);
        if (a != b) { // 최상위 노드가 다른경우, 합친다.
            if (a > b)
                parent[a] = b;
            else
                parent[b] = a;
        }
    }

    private static int find(int n) {
        if (parent[n] == n)
            return n; // 최상위 값이 현재값과 같다면, 현재값 Return
        else // 최상위 값이 현재와 다르다면, n은 다른 최상위 노드가 존재한다.
            return parent[n] = find(parent[n]); // 경로 압축.
        /*
         * 경로 압축
         * 경로 압축을 하지 않는다면, 트리구조의 하위 항목으로 계속 내려가게 된다.
         * 하지만, Union-Find에서 중요한것은 현재의 Detph가 아닌 최상위 노드가 무엇인지를 찾는것이다.
         * Depth를 깊게(세로로 긴 형태) 보다는 Width를 넓게 ( 가로로 긴 형태)로 만들자.
         * 세로가 긴 형태는 O(n)에 수렴할 수 있다.
         * 반면 가로가 긴 형태는 O(1)에 수렴한다.
         */
    }

    private static void makeSet(int n) {
        parent = new int[n + 1];
        for (int i = 1; i <= n; ++i)
            parent[i] = i; // 최초 각 원소의 최상위 노드는 자기 자신이다.
    }
}

C++

#define N 5

#include<iostream>
using namespace std;


int parent[N + 1] = {};

int find(int n)
{
	if (parent[n] == n)
		return n;
	else
		return parent[n] = find(parent[n]);
}

void makeSet(int n)
{
	for (int i = 1; i <= n; ++i) {
		parent[i] = i;
	}
}

void unionSet(int a, int b)
{
	a = find(a);
	b = find(b);
	if (a != b)
	{
		if (a > b)
			parent[a] = b;
		else
			parent[b] = a;
	}
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);

	// Step1. MakeSet
	makeSet(N);

	// Step2. Find
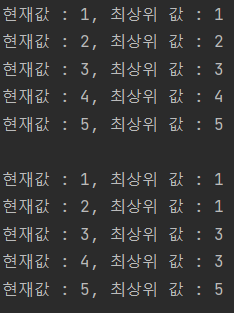
	for (int i = 1; i <= N; ++i)
		cout << "현재값 : " << i << ", 최상위 값 : " << parent[i] << endl;

	// Step3. Union
	unionSet(1, 2);
	unionSet(3, 4);

	cout << endl;
	// Step4. Find
	for (int i = 1; i <= N; ++i)
		cout << "현재값 : " << i << ", 최상위 값 : " << parent[i] << endl;
	return 0;

}