문제

https://www.acmicpc.net/problem/2133

3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.

---

입력

첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.

---

출력

첫째 줄에 경우의 수를 출력한다.

---

풀이

접근방법

시간제한 2초, 메모리 128MB이다.

N이 홀수와 짝수일때를 우선 구분해보자.

• N이 홀수라면.
  타일의 크기는 2, 채워야할 공간의 수는 3,6,9 ...
  1칸이 비어 채울 수 없다.

if N == 홀수
dp[i] = 0

• N이 짝수라면

N==2 라면 아래 3가지의 방법이 가능하다.

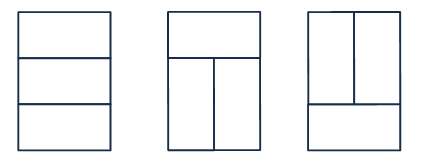
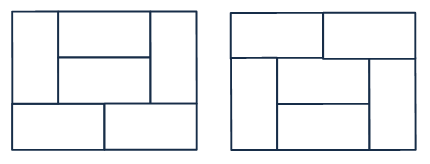
N==4 라면, N이 2일때를 붙인것과 추가적으로 아래와 같은 특수한 모양이 2개 추가된다.
3x3 + 2 = 11

N==6
아래와 같이 2개와 4개로 나누어서 채우는 방법을 생각해본다.
11x3(2-4분할) + 3x2(4-2분할에서의 특이케이스) + 2(특수모양) = 41

2-4분할과 4-2분할을 왜 따로 계산하느냐? 라고 생각할 수 있다.
2-4 분할에서의 4는 4로 만들 수 있는 모든 경우의 수가 포함되어있다.
그리고 반대 4-2분할을 할 때 모든 경우의 수로 계산을 하면 중복이 발생한다. 나머지 한쪽의 4를 그릴때는 아래와 같은 모양으로 4가 채워진 경우만 계산하기 위함이다.
( 아래 모양은 가로 4칸에 걸쳐 생성되는 것 )

N이 2,4,6...일때를 한번 생각해보자.

N	경우의 수
0	0
1	0
2	3
3	0
4	11
5	0
6	41

N과 경우의 수를 살펴보고 점화식을 찾아보자.

i==짝수
	dp[i] = dp[i - 2] * 4 - dp[i - 4]
i==홀수
	dp[i] = 0

---

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {

	static int N;
	static int[] dp;

	public static void main(String[] args) throws IOException {
		BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

		N = stoi(in.readLine());
		dp = new int[31];
		dp[0] = 0;
		dp[2] = 3;
		dp[4] = 11;

		for (int i = 6; i <= N; i+=2)
			dp[i] = dp[i - 2] * 4 - dp[i - 4];
            
		System.out.println(dp[N]);
	}

	private static int stoi(String s) {
		return Integer.parseInt(s);
	}
}