최소 신장 트리(MST, Minimal Spanning Tree)

개요

Minimal Spanning Tree,
신장 트리는 그래프에서 모든 정점에 대한 최소한의 연결만을 남긴 그래프이다. 최소 비용 신장 트리는 신장 트리들 중 간선의 가중치 합이 가장 작은 트리이다.
즉. 그래프의 모든 노드를 사이클 없이 모두 연결할때, 최소 비용을 가지는 것.

설명

• 그리디 기법을 적용해서 최적의 해를 구할 수 있으며, 주로 알려진 방법은 크루스칼(Kruskal)과 프림(Prim) 알고리즘이 있다.

크루스칼(Kruskal)

• 간선의 수가 작다면 크루스칼이 유리하다. O(ElogE)

1. 간선 데이터를 비용에 따라 정렬한다.

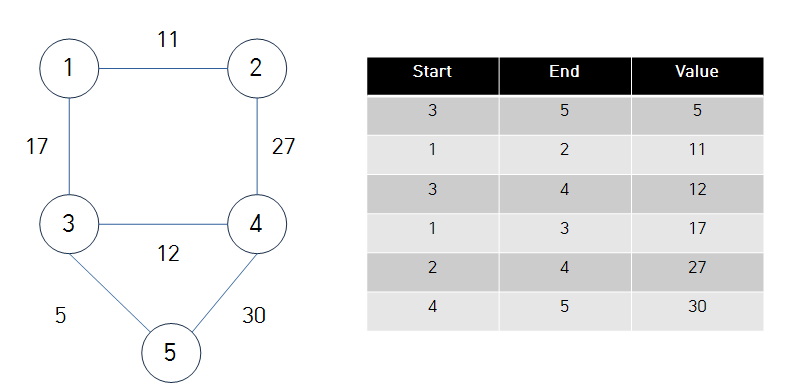
• 첫번째 방법. Priority Queue를 활용하기.
• 두번째 방법. Quick Sort를 활용하기.

2. 간선을 하나씩 확인하며, 해당 노드들이 연결되지 않았다면 연결한다.

3. 2번의 과정을 반복한다.

• 연결은 Disjoint-Set(Union-Find를 활용한다)

1. 3-5 두 노드의 최상위 노드가 다르다. 연결.
   
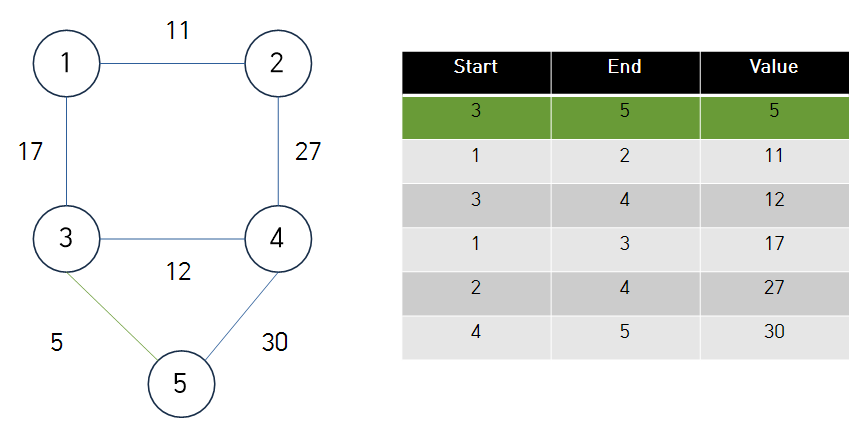
2. 1-2 두 노드의 최상위 노드가 다르다. 연결.
   
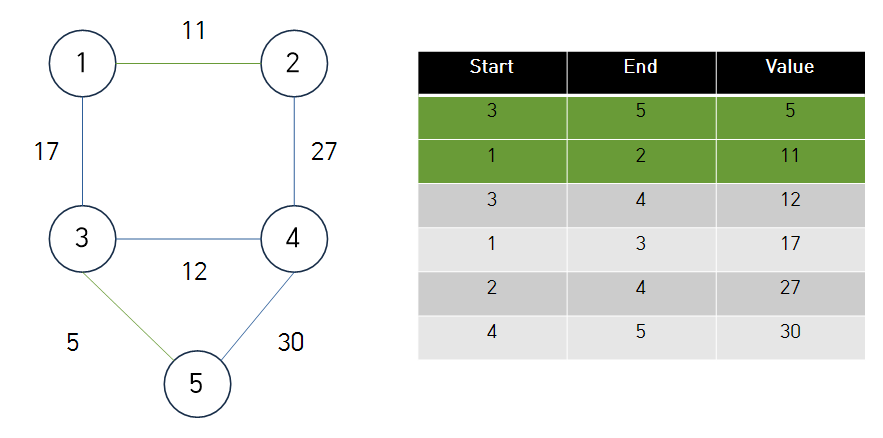
3. 3-4 두 노드의 최상위 노드가 다르다. 연결.
   
4. 1-3 두 노드의 최상위 노드가 다르다. 연결.
   
5. 2-4의 경우, 두 노드의 최상위 노드가 같다. ( 연결 시 사이클 발생) 따라서 연결하지 않는다.
   
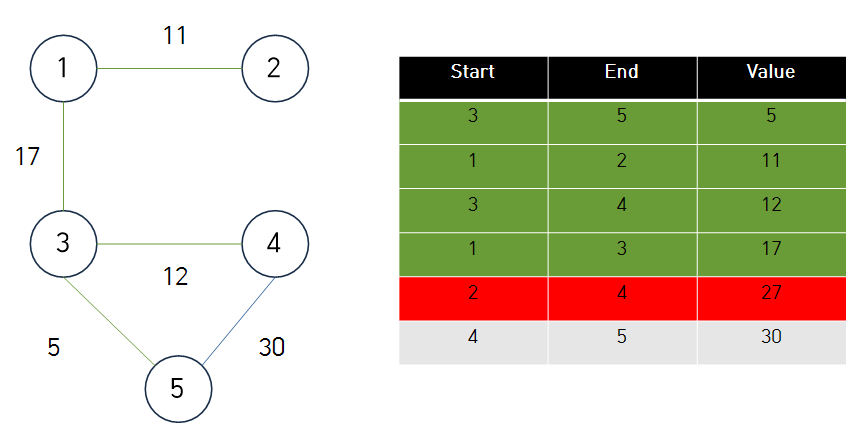
6. 4-5의 경우, 두 노드의 최상위 노드가 같다. ( 연결 시 사이클 발생) 따라서 연결하지 않는다.
   

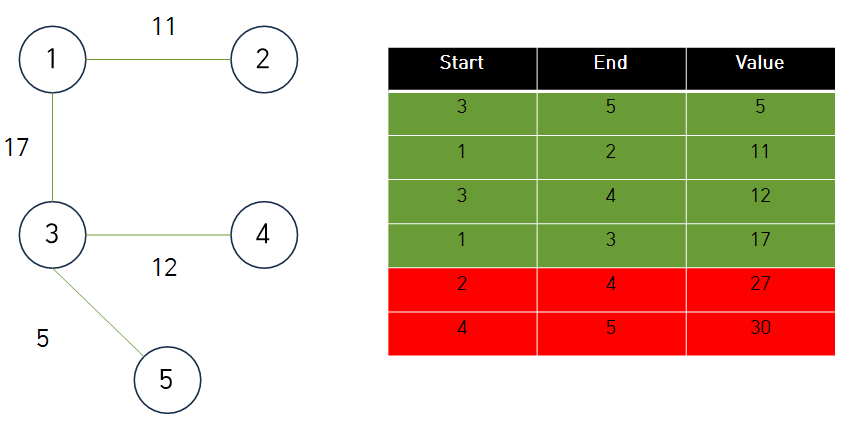
따라서 MST의 비용은 45가 된다.

프림(Prim)

• 간선의 수가 많다면 프림이 유리하다.
  (작성중..)

코드

• 어떤 언어를 사용할 지 몰라 둘 다 준비했다.

Java - Kruskal

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.PriorityQueue;

public class Main {
	static class Node implements Comparable<Node> {
		int start;
		int end;
		int value;

		Node(int a, int b, int c) {
			start = a;
			end = b;
			value = c;
		}

		public int compareTo(Node n) {
			return value - n.value;
		}
	}

	static int parent[];
	static int N, M;

	public static void main(String[] args) throws IOException {
		BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

		String[] splitedLine = in.readLine().split(" ");
		N = Integer.parseInt(splitedLine[0]);
		M = Integer.parseInt(splitedLine[1]);

		init();
		PriorityQueue<Node> pq = new PriorityQueue<>();
		for (int i = 0; i < M; ++i) {
			splitedLine = in.readLine().split(" ");
			pq.add(new Node(Integer.parseInt(splitedLine[0]), Integer.parseInt(splitedLine[1]),
				Integer.parseInt(splitedLine[2])));
		}
		int value = 0;
		while (!pq.isEmpty()) {
			Node node = pq.poll();
			if (find(node.start) != find(node.end)) {
				union(node.start, node.end);
				value += node.value;
			}
		}

		System.out.println(value);

	}

	public static void init() {
		parent = new int[N];
		for (int i = 0; i < N; ++i) {
			parent[i] = i;
		}
	}

	public static void union(int a, int b) {
		a = find(a);
		b = find(b);

		if (a < b)
			parent[b] = a;
		else
			parent[a] = b;
	}

	private static int find(int n) {
		if (n == parent[n])
			return n;
		else
			return parent[n] = find(parent[n]);
	}
}

C++

// 작성중..