Backpropagation

Why Backpropagation

Neural Network는 Layer 여러 개로 이루어져 있기 때문에 일반적인 Gradient descent와는 다르다.

• 중첩된 Layer가 아닐 때 $w_{t+1}:=w_t-lr\frac{\partial\text{Loss}}{\partial w}$
• Neural Network는 파라미터화 된 function의 sequence이다.
  $x \rightarrow \theta_1 \rightarrow \text{output}_1 \rightarrow \theta_2 \rightarrow \text{output}_2 \rightarrow \text{linear} \rightarrow \cdots$
• Parameters는 loss를 최소화해야 한다.
  $\min_\theta\frac{1}{N}\sum_{i=1}^{N}L(h(x_i;\theta))_,y_i)$
  • 이때 $h(x_i;\theta)$는 Neural network를 의미한다.
• Gradient descent를 통한 최소화는 gradient를 계산해야 한다.
  $\theta^{(t+1)}=\theta^{(t)}-\lambda\frac{1}{N}\sum_{i=1}^{N}\nabla L(h(x_i;\theta),y_i) \\ \text{ }\\ z=h(x;\theta) \\ \text{ }\\ \nabla L(h(x_i;\theta),y_i)=\frac{\partial L(z,y)}{\partial z}\frac{\partial z}{\partial \theta}$
  • $\frac{\partial z}{\partial \theta}$는 해당 $z$에 미치는 $\theta$의 영향을 의미한다.
• Backpropagation: $\frac{\partial z}{\partial \theta}$를 계산하는 방법

Backpropagation이 있어야 Neural network 학습이 가능하다.

The Gradient of Neural Network

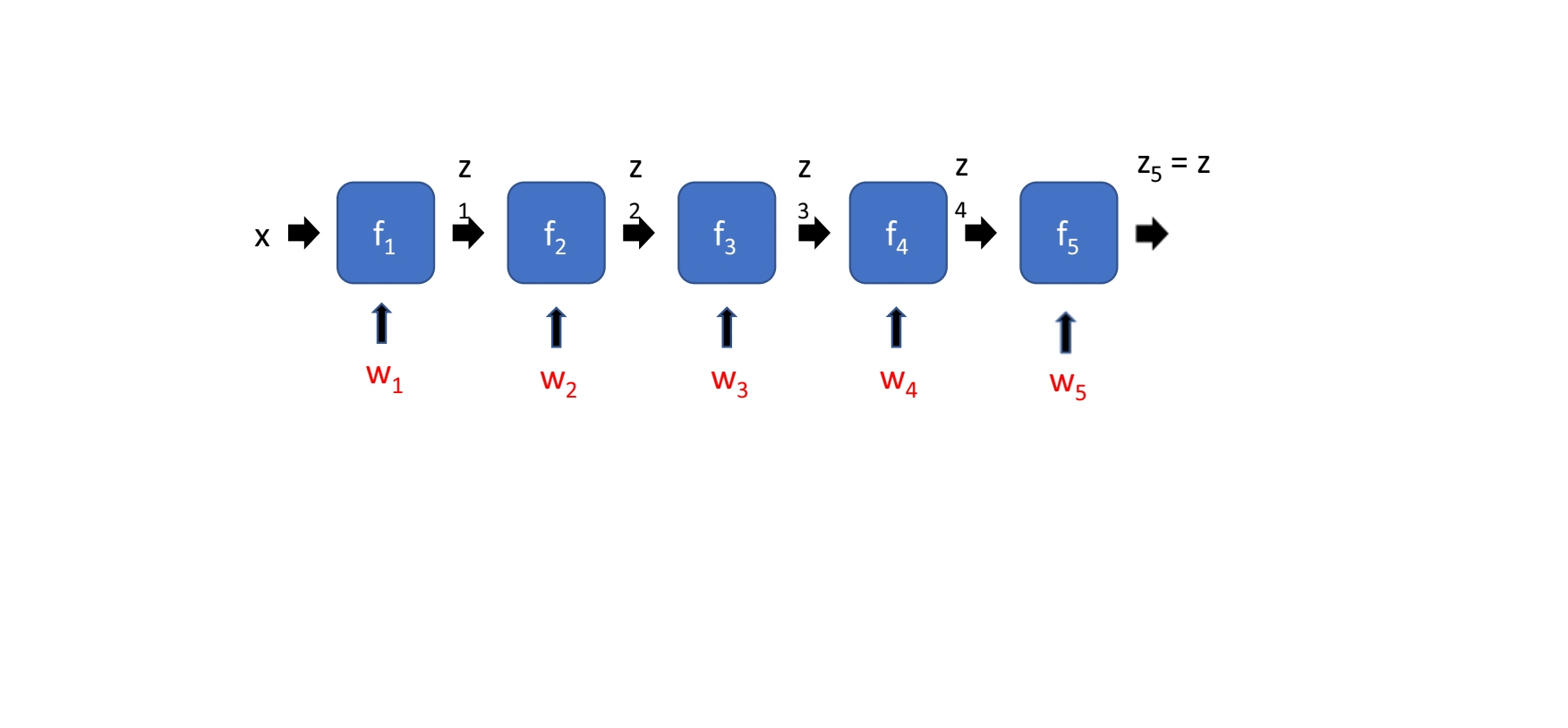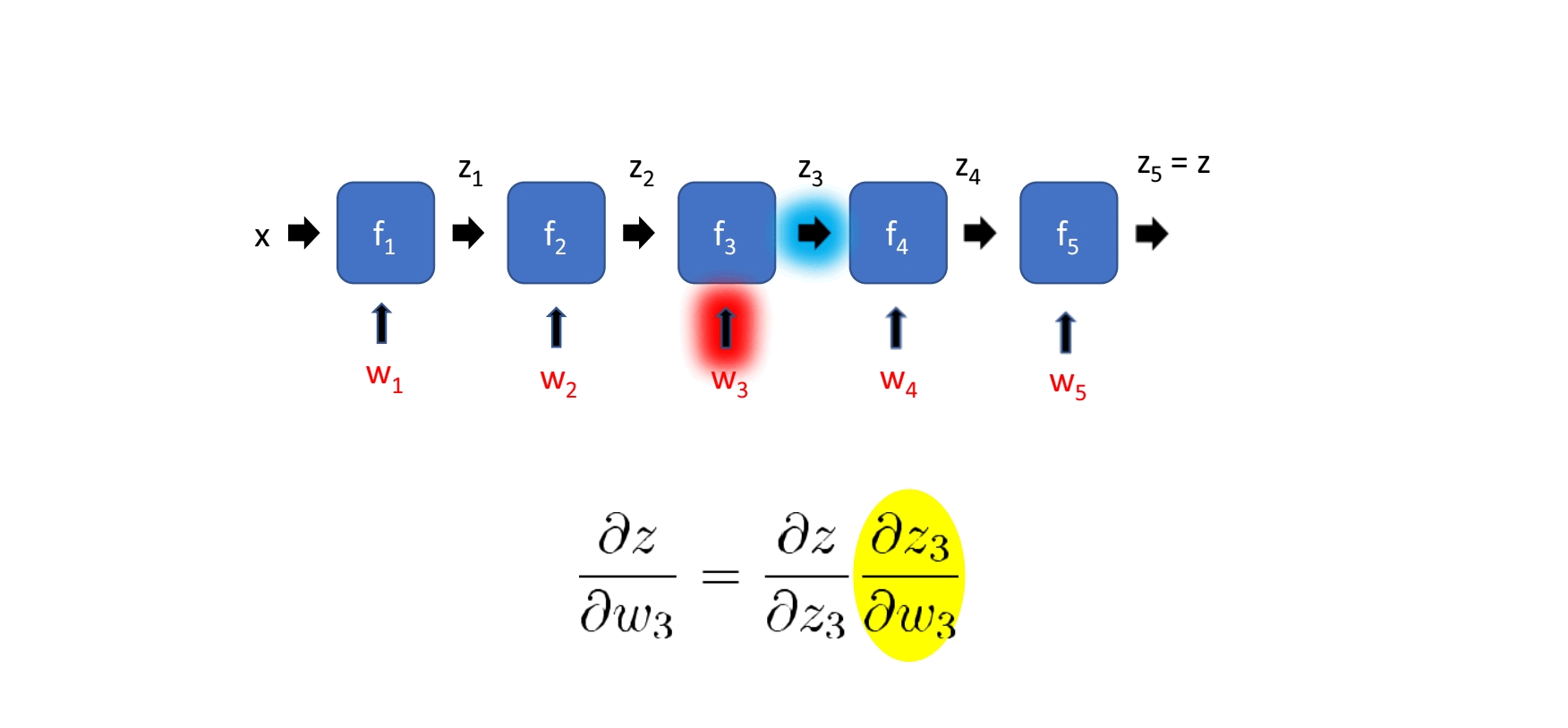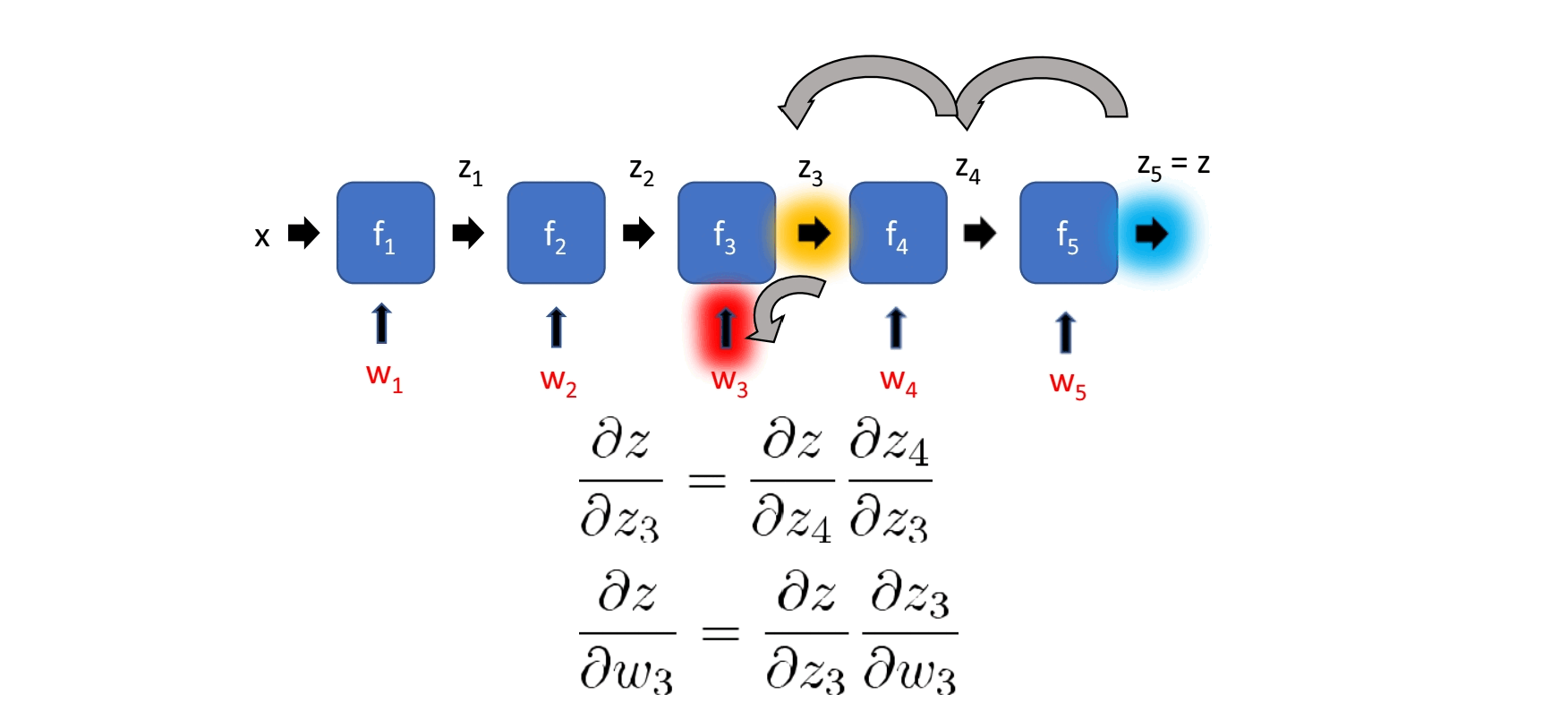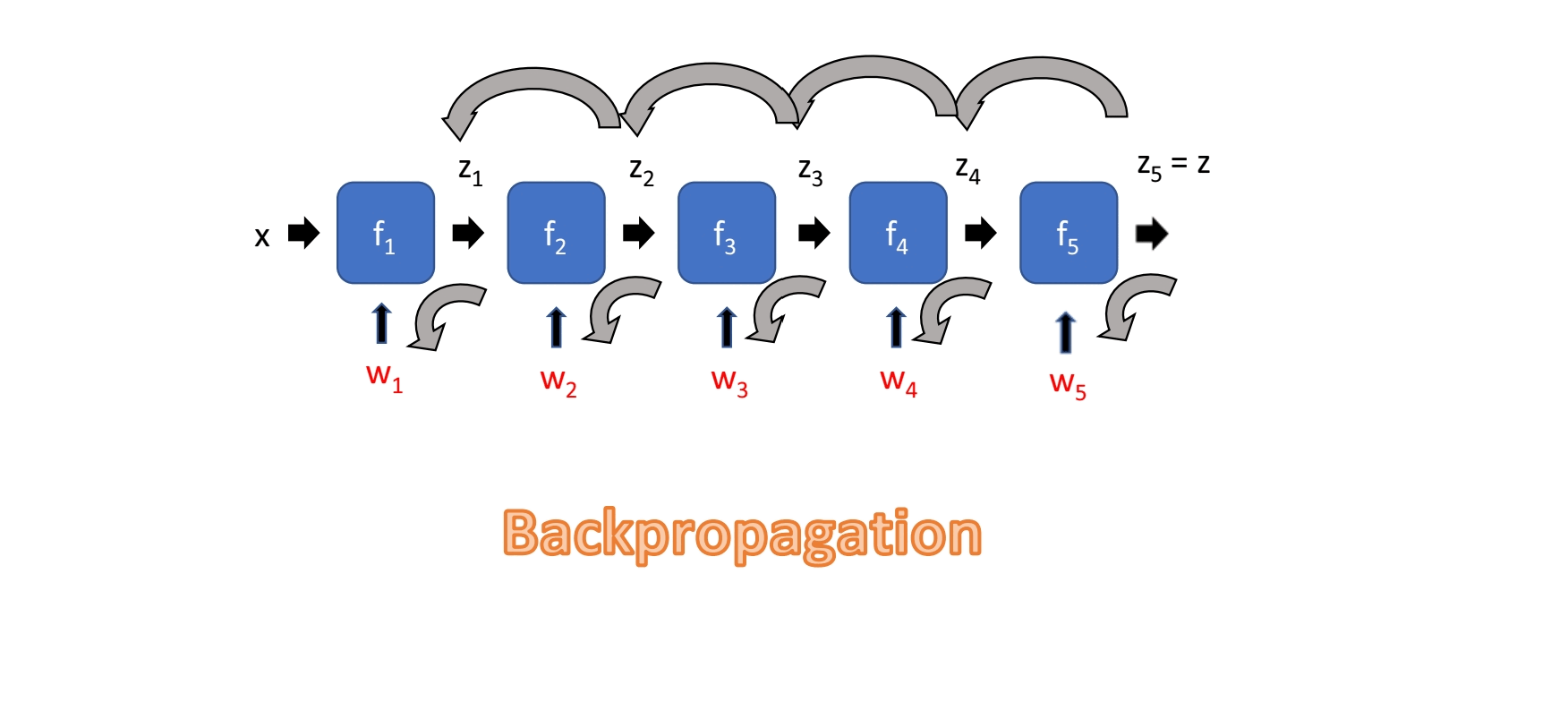
Input $x$에 가까워질수록 계산량이 많아진다.

• 대부분 1 이하의 값이기 때문에 update해도 큰 변화가 없다.

Backpropagation for a Sequence of Functions

$z_i=f_i(z_{i-1},w_i)\\ z_0=x\\ z=z_n$

• 각 Function을 미분할 수 있다고 가정
  $\frac{\partial z_i}{\partial z_{i-1}}=\frac{\partial f_i(z_{i-1},w_i)}{\partial z_{i-1}}$
  $\frac{\partial z_i}{\partial w_i} = \frac{\partial f_i(z_{i-1},w_i}{\partial w_i}$
• $z$의 gradient를 저장하기 위해 $g(z_i)$, $w_i$의 gradient를 저장하기 위해 $g(w_i)$를 사용한다.
  $g(z_n)=\frac{\partial z}{\partial z_n}=1$
  $g(z_{i-1})=\frac{\partial z}{\partial z_i}\frac{\partial z_i}{\partial z_{i-1}}=g(z_i)\frac{\partial z_i}{\partial z_{i-1}}$
• Parameter의 Gradient를 계산하기 위해 $g(z_i)$를 사용한다.
  $g(w_i)=\frac{\partial z}{\partial z_i}\frac{\partial z_i}{\partial w_i}=g(z_i)\frac{\partial z_i}{\partial w_i}$

Loss as a Function

Training of Nerual Network

1. Sample Image and Label
2. Forward: Image는 Network를 거쳐 Loss를 계산한다.
3. Backward: Gradients를 계산하기 위해 Backpropagetion
4. Weights를 업데이트하기 위해 Gradient 반대 방향으로 이동한다.

Computation Graphs

• 중간 output과 parameter 간의 구분 없는 임의의 예시 그래프
• 각 node에서는 두 개의 funeciot이 동작한다.
  • Forward: 주어진 input에서 output을 계산한다.
  • Backward: 출력에 대한 z의 도함수가 주어지면 입력에 대한 z의 도함수를 계산한다.
• 입력 $a, b, c$에 대한 함수 $f_i$의 출력이 $d$일 때 Backward
  $\frac{\partial z}{\partial d} \rightarrow \big[ \frac{\partial z}{\partial a}, \frac{\partial z}{\partial b}, \frac{\partial z}{\partial c} \big]$

Feed-Forward Networks

Network를 통해 Prediction으로 feed forward 되어 Classification이 이루어진다.

• ex) P 차원 데이터
  
  • 모든 node는 Input의 영향을 받는다.

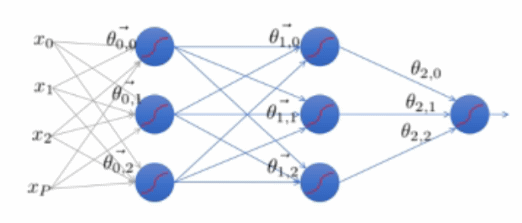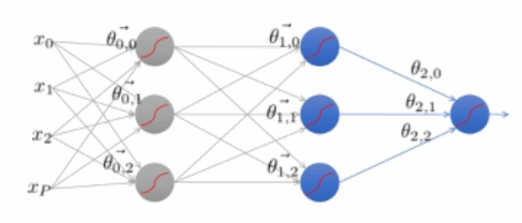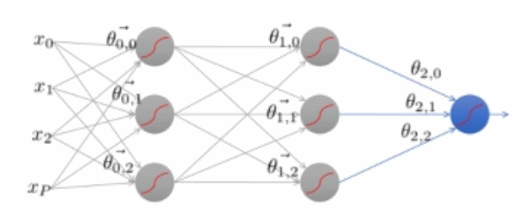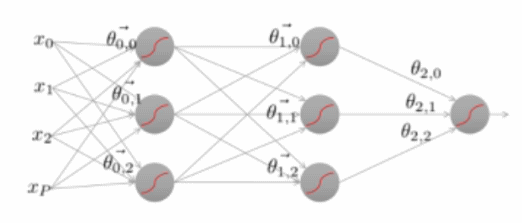
Error Backpropagation

Network 전체에서 Gradient descent 수행 과정

• Training은 마지막 레이어에서 첫번째 레이어 순서로 진행된다.

1. 각 layer의 파라미터를 재정의한다.
   $\vec{\theta}=\{w_{ij}, w_{jk}, w_{kl}\}$
   
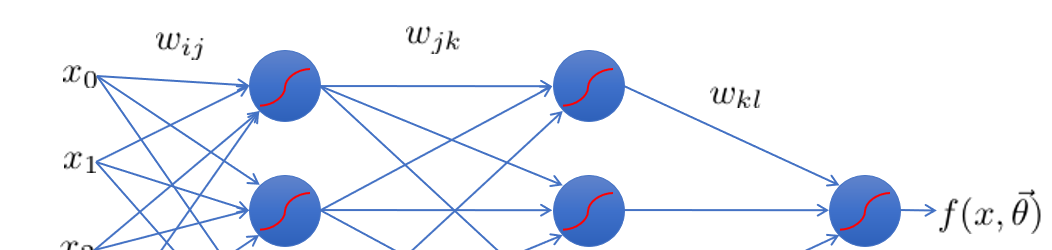
2. 각 node의 입력과 출력을 구분한다.
   

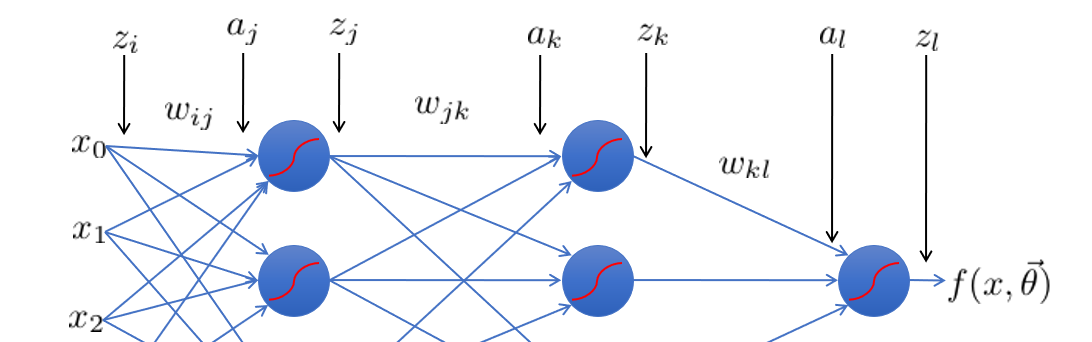
• $z_t$는 각 layer의 연산 결과에 non-linear activateion function을 적용한 결과이다.
  $G(a_j)=z_j$

3. Linear Combination

   $a_j=\sum_i^Pw_{ij}z_i \quad a_k=\sum_jw_{jk}z_j \quad a_l=\sum_lw_{kl}z_k \\ z_j=g(a_j) \quad z_k=g(a_k) \quad z_l=g(a_l)$

4. 실제 값과 예측 값의 차이 계산 - Empirical Risk Function

   $R(\theta)=\frac{1}{N}\sum_{n=0}^{N}L(y_n-f(x_n)) \\ \qquad = \frac{1}{N}\sum_{n=0}^{N}\frac{1}{2}(y_n-f(x_n)) \\$

   $R(\theta)=\frac{1}{N}\sum_{n=0}^{N}\frac{1}{2}\Big( y_n-g \Big( \sum_kw_{kl}g\big( \sum_jw_{jk}g(\sum_iw_{ij}x_{n,i})\big) \Big ) \Big)^2$

5. 마지막 layer의 weight 최적화
   $N$은 데이터의 수를 의미하며, 모든 데이터를 활용하여 gradient를 계산해야 한다.

   • Calculus chain rule
     $\frac{\partial R}{\partial w_{kl}}=\frac{1}{N}\sum_n\Big[ \frac{\partial L_n}{\partial a_{l,n}} \Big]\Big[ \frac{\partial a_{l,n}}{\partial w_{kl}} \Big]$
     가중치 $w$는 데이터의 수와 무관하기 때문에 $n$ index가 없다.
   • 함수 전개
     $\frac{\partial R}{\partial w_{kl}}=\frac{1}{N}\sum_n\Big[ \frac{\partial \frac{1}{2}(y_n-g(a_{l,n}))^2}{\partial a_{l,n}} \Big]\Big[ \frac{\partial z_{k,n}w_{kl}}{\partial w_{kl}} \Big]$
   • 미분 계산
     $\frac{\partial R}{\partial w_{kl}}=\frac{1}{N}\sum_n [-(y_n-z_{l,n})g'(a_{l,n})]z_{k,n}$
   • 식 요약
     $\frac{\partial R}{\partial w_{kl}}=\frac{1}{N}\sum_n \delta_{l,n}z_{k,n}$

6. 마지막 hidden layer의 weight 최적화

   • Calculus chain rule
     $\frac{\partial R}{\partial w_{jk}}=\frac{1}{N}\sum_n\Big[ \frac{\partial L_n}{\partial a_{k,n}} \Big]\Big[ \frac{\partial a_{k,n}}{\partial w_{jk}} \Big]$
   • Multivariate Chain rule
     $\frac{\partial R}{\partial w_{jk}}=\frac{1}{N}\sum_n\Big[ \sum_l \frac{\partial L_n}{\partial a_{l,n}} \frac{\partial a_{l,n}}{\partial a_{k,n}} \Big] \Big[ \frac{\partial a_{k,n}}{\partial w_{jk}} \Big]$
   • 치환
     $\frac{\partial R}{\partial w_{jk}}=\frac{1}{N}\sum_n\Big[ \sum_l \delta_l \frac{\partial a_{l,n}}{\partial a_{k,n}} \Big] \big[ z_{j,n} \big]$
   • 미분 계산
     $\frac{\partial R}{\partial w_{jk}}=\frac{1}{N}\sum_n\Big[ \sum_l \delta_l w_{kl} g'(a_{k,n}) \Big] \big[ z_{j,n} \big]$
   • 식 요약
     $\frac{\partial R}{\partial w_{jk}}=\frac{1}{N}\sum_n\big[ \delta_{k,n} \big] \big[ z_{j,n} \big]$

7. 남은 이전 layers에 대해 반복한다.

   $\frac{\partial R}{\partial w_{ij}}=\frac{1}{N}\sum_n\big[ \delta_{j,n} \big] \big[ z_{i,n} \big]$

8. 각 parameter에 대해 gradient를 계산했으므로 parameter를 업데이트 한다.

   $w_{ij}^{t+1}=w_{ij}^{t}-\eta\frac{\partial R}{w_{ij}} \\ w_{jk}^{t+1}=w_{jk}^{t}-\eta\frac{\partial R}{w_{jk}} \\ w_{kl}^{t+1}=w_{kl}^{t}-\eta\frac{\partial R}{w_{kl}}$

Summary

• Error backprop은 Multivariate Chain을 해결하고 각 구성요소에 대한 gradient를 개별적으로 해결한다.
• 각 layer의 target values는 다음 layer에서 부터 온다.
• Error backprop은 network에서 뒤로 error를 전달한다.