Bagging, Boosting

Ensembling methods

여러 model을 한 번에 사용하는 방법

• 하나의 model을 사용하는 것보다 나은 성능을 보인다.
• Linear, Logistic, NN 등 다양한 model을 사용할 수 있다.

1. Bagging: 학습 데이터 전체를 사용하지 않고 sampling하여 여러 model을 학습한다.
2. Boosting: 순차적으로 이전에 틀린 sample에 weight를 가하며 model을 학습한다.

• Bagging과 Boosting은 서로 다른 목적을 가진다.

Bias/Variance Decomposition(Tradeoff)

• $y$: random variable $x$에 대한 예측
  • 예측의 불확실성을 포함하여 확률적으로 표현된다.
• $y_\star$: 주어진 $x$에 대해 $y$가 반환할 수 있는 최선의 예측값
  • optimal deterministic prediction
• $t$: label
  • $t=y_\star(x) + e$
• $E[{(y-t)}^2]$: model의 오류로, 낮을수록 fit model이라고 할 수 있다.

$E[{(y-t)}^2]$
$E[y^2+t^2-2yt]$	곱셈공식
$E[y^2]+E[t^2]-2E[yt]$
$Var[y]+E[y]^2+Var[t]+E[t]^2-2E[y(y_\star+e)]$	$E[X^2]=Var[X]+E[X]^2$ 관계, $t=y_\star+e$
$Var[y]+Var[t]+E[y]^2+{y_\star}^2-2y_\star E[y]$	$e\sim N(0,\sigma^2)$
$Var[t] + Var[y] + (y_\star-E[y])^2$
Bayes error + variance + bias	Bias/Variance Decomposition

• bias: prediction이 얼마나 틀리는가
  • 얼마나 underfitting 되었는가
• variance: prediction의 variability
  • 얼마나 overfitting 되었는가
• 일반적으로 bias와 variance는 tradeoff 관계이다.
• Bayes error: 바꿀 수 없는 값, label t의 분포
• Bias/Variance Decomposition: Visualization
  
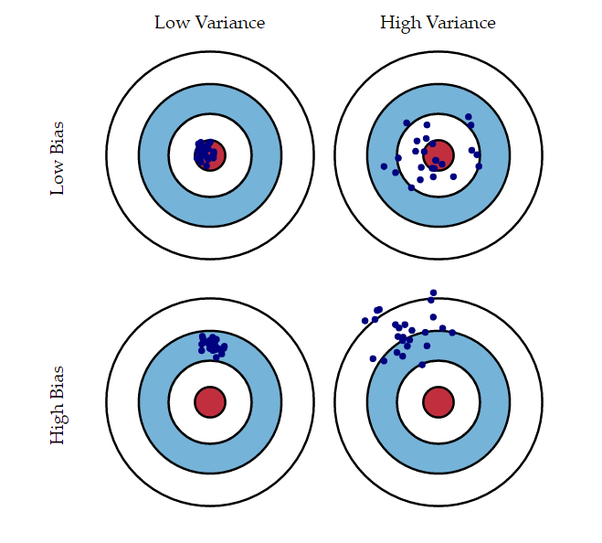
  • Low Bias, Low Variance: 가장 이상적인 결과
  • Low Bias, High Variance: Bagging으로 해결
  • High Bias, Low Variance: Ada Boosting으로 조정 가능
    • 안정적이지만 성능이 낮은 모델

Bias/Variance Decomposition은 squared error에만 적용되지만, bias와 variance를 Overfitting과 Underfitting의 동의어로 사용한다.

Bagging

Motivation

• $p_\text{sample}$로부터 $m$개의 독립적인 training sets로 sampling 할 수 있다고 가정한다.
• 각각에 대한 prediction $y_i$가 있고 전체 prediction은 평균으로 계산한다.
  $y=\frac{1}{m}\sum_{i=1}^{m}y_i$
• 위의 식이 loss에 끼치는 영향
  • Bayes error: unchanged
  • Bias: unchanged
    • 평균 prediction에는 변화가 없다.
      $E[y] = E\Big[\frac{1}{m}\sum_{i=1}^{m} y_i\Big] = E[y_i]$
  • Variance: 감소한다.
    • 독립적인 sample로부터 평균을 계산하기 때문이다.
      $Var[y]=Var\Big[\frac{1}{m}\sum_{i=1}^{m}y_i\Big]=\frac{1}{m^2}\sum_{i=1}^{m}Var[y_i]=\frac{1}{m}Var[y_i]$

The Idea

• sampling distribution $p_\text{sample}$ 문제점
  • Sampling은 시간적, 경제적으로 비용이 많이 나가는 작업이다.
  • 일반적으로 sampling을 할 data가 제한적이다.
• 독립적으로 추출된 datasets로 models를 나누어 학습하는 것은 data의 낭비이다.
  • 모든 sampled datasets로 하나의 model을 학습하는 것은 어떨까?

Solution: 주어진 training set $\mathcal{D}$가 있을 때 경험적 분포 $p_\mathcal{D}$를 $p_\text{sample}$의 대용으로 사용한다.

• $n$개의 데이터로 이루어진 하나의 dataset $\mathcal{D}$로 예를 든다면,
• $\mathcal{D}$에서 sampling하여 $m$개의 새로운 datasets(resamples of bootstrap samples)를 생성한다.
• 이 datasets에 대해 학습된 각 models의 predictions 평균을 계산한다.
• Intuition: $\text{As } |\mathcal{D}| \rightarrow \infin, \text{ we have } p_\mathcal{D} \rightarrow p_\text{sample}$

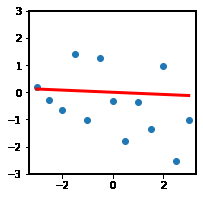
Effect on Hypothesis Space

여러 classifiers를 결합했을 때 original hypothesis space와 ensembled hypothesis의 차이가 확연하게 드러난다.

Sampled datasets & Fitted hypothesis	Ensembled hypothesis

Bagging for Binary Classification

• classifiers의 출력값이 실제 확률 값 $z_i \in [0,1]$이라면, 다음과 같이 계산할 수 있다.
  $y_\text{bagged}=\mathbb{I}(z_\text{bagged}\gt 0.5)=\mathbb{I}\Big( \sum_{i=1}^{m}\frac{z_i}{m} \gt 0.5 \Big)$
  • 확률 값 $z_i$의 평균이 0.5 이상이면 True로 계산한다.
• classifiers의 출력값이 binary decision $y_i \in \{0,1\}$이라면, 위와 똑같이 평균으로 계산할 수 있다.
  $y_\text{bagged}=\mathbb{I}\Big( \sum_{i=1}^{m} \frac{y_i}{m} \gt 0.5\Big)$
• 다수결과 동일한 계산 방법
• Bagged Classifier는 평균적인 underyling model 보다 더 강력하다.
  • 개인이 아닌 청중에게 물어보아야 더 효과적인 것과 같은 맥락

Effect of Correlation

• Problem: Datasets는 독립적이지 않기 때문에 variance를 1/$m$으로 줄일 수 없다.
  • sampled predictions의 분산이 $\sigma^2$이고 상관관계가 $\rho$일 때
    $Var\Big( \frac{1}{m}\sum_{i=1}^{m}{y_i} \Big) = \frac{1}{m}(1-\rho)\sigma^2+\rho\sigma^2$
  • model 간의 상관관계가 없을수록 높은 성능을 보인다.
• 모순적이게도 samples 간의 상관관계를 줄이는 한에서, 알고리즘에 추가적인 변동성(예측의 불확실성)을 도입하는 것이 유리할 수 있다.
  • Intuition: 여러 알고리즘을 사용하는 것이 평균 계산에 도움이 된다.

Limitations

• Squared error를 사용한 경우 bias를 줄일 수는 없다.
• classifiers의 상관관계가 여전히 남는다.
  • 상관관계가 높을수록 성능이 안 좋다.
• Naive Mixture
  • members가 서로 매우 다르다면 weighted ensembling을 통해 더 나은 결과를 얻을 수 있다.

Boosting

• Classifiers를 순차적으로 학습시키며, 매번 이전 classifier가 틀린 training examples에 집중한다.
• 특정 examples에 집중하기 위해서 weighted training set을 사용한다.

Weighted Training set

• Classifier의 오류 rate는 다음과 같이 계산한다.
  $\frac{1}{N}\sum_{n=1}^{N}\mathbb{I}[h(x^{(n)} \ne t^{(n)}]$

  $h(x)$	$t$	$\mathbb{I}[h(x)\ne t]$
  0	0	맞혔으므로 0
  0	1	틀렸으므로 1
  1	0	틀렸으므로 1
  1	1	맞혔으므로 0

• Key idea: 각 examples에 서로 다른 weight를 가하여 model을 학습한다.

  • Classifier는 높은 가중치를 이용하여 틀렸던 것도 맞을 수 있도록 학습한다.
    $\sum_{n=1}^{N}\mathbb{I}[h(x^{(n)} \ne t^{(n)}] \text{ becomes } \sum_{n=1}^{N}w^{(n)}\mathbb{I}[h(x^{(n)} \ne t^{(n)}]$

• 일반적으로 $w^{(n)}$는 0보다 크며, $w{(n)}$의 총합은 1이다.

AdaBoost(Adaptive Boosting)

• The key steps of AdaBoost
  1. 매 반복에서 model이 틀린 samples의 가중치를 조정한다.
  2. 새로 가중치가 계산된 samples로 새로운 base classifier를 학습한다.
  3. 학습된 base classifier의 적절한 가중치를 부여하여 ensemble classifiers에 추가한다.
  4. 수차례 반복한다.
• Requirements for base classifier
  • weighted error를 최소화해야 한다.
  • Ensemble은 매우 커질 수 있으므로 base classifier는 빨라야 한다.
    • 정확도가 최소 51%인 weak learner를 사용하여도 충분하다.
• Weak learners를 underfit 상태이므로 높은 bias를 가진다.
  • 각 classifier가 틀린 문제에 집중함으로써 AdaBoost가 bias를 줄일 수 있다.

Weak Learner

• (비공식적 설명) Weak learner는 binary label case에서 정확도가 0.51 정도로 우연보다 성능이 약간 더 좋은 learning algorithm을 뜻한다.

Weak Classifiers

• Input: Data $\mathcal{D}_N=\{ x^{(n)},t^{(n)} \}_{n=1}^N$, $t^{(n)} \in \{ -1, +1 \}$
• Weak Classifier $h$
  • Weak classifier 단 하나를 사용하는 것은 training error를 줄이도록 학습하는 데에 적절하지 않다.
  • 우연보다는 나은 성능을 보인다면 AdaBoost는 전체 function의 근사치를 구할 수 있다.
• 0-1 loss: $\mathbb{I}[h(x^{(n)}\ne t^{(n)}]=\frac{1}{2}(1-h(x^{(n)}) \cdot t^{(n)})$
  • 틀리면 1, 맞히면 0
• Output: Classifier $H(x)$
• Initialize sample weights: $w^{(n)}=\frac{1}{N} \text{ for } n=1, \cdots, N$
• 다음을 $T$ 만큼 반복한다.
  1. classifier $h_t$를 학습한다.
     $h_t \leftarrow \argmin_{h\in \mathcal{H}} \sum_{n=1}^N w^{(n)}\mathbb{I}\{ h(x^{(n)}) \ne t^{(n)} \}$
     • 틀린 예측에 대해 그 데이터의 가중치를 곱한 값을 줄이는 방향으로 학습한다.
  2. 학습한 모델의 weighted error를 계산한다.
     $\text{err}_t=\frac{\sum_{n=1}^{N}w^{(n)}\mathbb{I}\{ h_t(x^{(n)}) \ne t^{(n)} \}}{\sum_{n=1}^{N}w^{(n)}}$
  3. classifier $h_t$의 신뢰도 계수를 계산한다.
     $\alpha_t=\frac{1}{2}\log{\frac{1-\text{err}_t}{\text{err}_t}}$
     
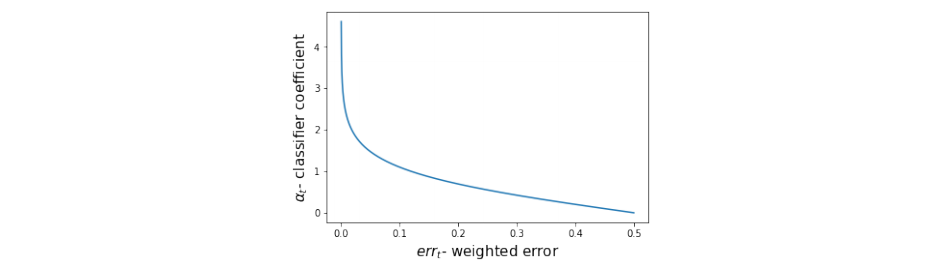
     • error가 낮을수록 신뢰도($\alpha_t$)가 커진다.
  4. Data sample의 가중치를 업데이트한다.
     $w^{(n)}\leftarrow w^{(n)}\exp\Big( -\alpha_tt^{(n)}h_t(x^{(n)}) \Big)$
     • 틀리면 모델의 신뢰도만큼 가중치가 커진다.
     • 맞으면 $\exp(\text{음수})$가 되어 가중치가 유지된다.
     • 좋은($\alpha_t$가 큰) classifier가 틀린 sample이라면 매우 어려운 sample이므로 중요도가 높다고 볼 수 있다.
• $H(x)$를 반환한다.
  $H(x) = \text{sign}\Big( \sum_{t=1}^{T} \alpha_th_t(x) \Big)$
  • 양, 음(sign)으로 판별하는 최종 model 반환
  • 최종 model은 모든 base model을 사용해야한다.
  • Variance는 조금 늘어날 수 있으나 bias는 확실하게 줄어든다.

Example

ex) 열 개의 데이터와 두 개의 weak classifiers가 있을 때 Boosting 과정

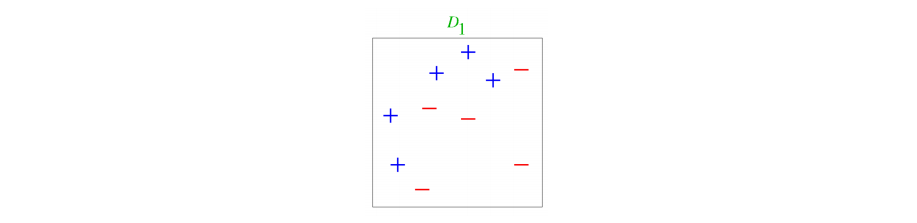
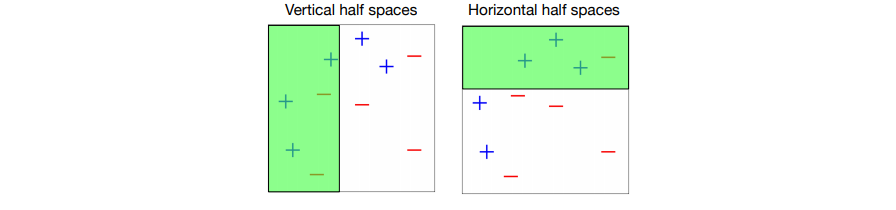
• 각각 틀린 data가 4개, 3개이므로 base classifier로 사용할 수 있다.

1. Round 1
   • $h_1$을 학습한 후 data의 가중치를 update한다.
     
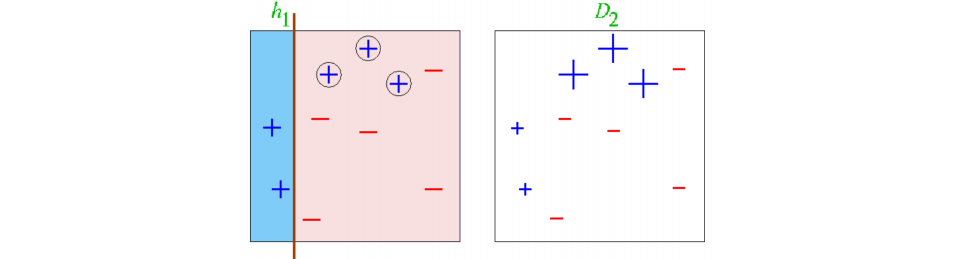
   • 모델의 신뢰도를 계산한다.
   • $H(x)=\text{sign}(\alpha_1h_1(x))$
2. Round 2
   • $h_2$를 학습한 후 data의 가중치를 update한다.
     
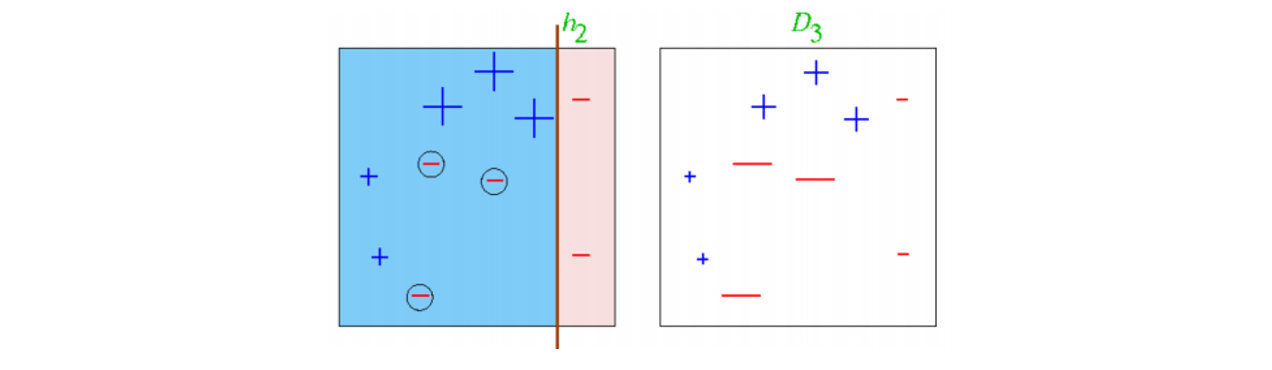
   • 모델의 신뢰도를 계산한다.
   • $H(x)=\text{sign}(\alpha_1h_1(x)+\alpha_2h_2(x))$
3. Round 3
   • $h_3$을 학습한 후 data의 가중치를 update한다.
     
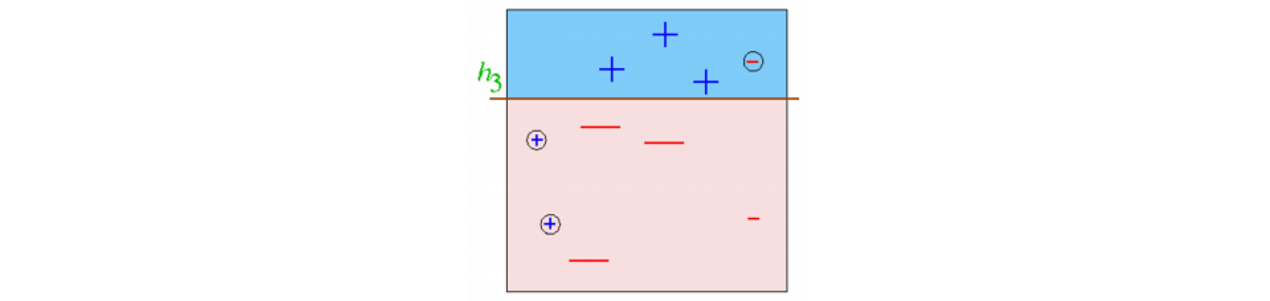
   • 모델의 신뢰도를 계산한다.
   • $H(x)=\text{sign}(\alpha_1h_1(x)+\alpha_2h_2(x)+\alpha_3h_3(x))$
4. Final Classifier $H$
   
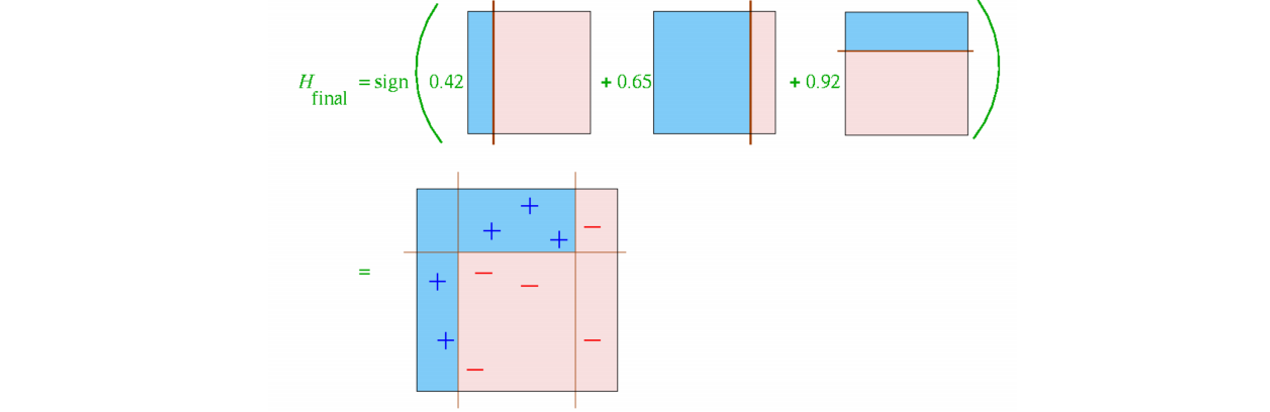
   • 최종 error는 0

Limitation

• Variance가 높아질 수 있다. 즉, overfittng이 발생할 수 있다.
• Ensemble elements 간의 의존성이 높다.
  • $\alpha_t$가 낮아도 사용하지 않으면 성능이 감소할 수 있으므로 반드시 사용해야 한다.