Generative Adversarial Network

Generative Adversarial Network

경쟁을 통한 생성형 모델

• 두 개의 모델이 동시에 학습된다.
• Generator가 학습하면서 Discriminator도 학습한다.
• generative mode G는 discriminator를 속여 True를 반환할 수 있도록 학습한다.
  • 실제 data의 분포를 capture할 수 있도록 학습한다.
• discriminative mode D는 generator가 만들어낸 모든 것을 False라 하도록 학습한다. G에 비해 학습이 빠르다.
  • $x \sim p_{data}$, then $D(x;\theta_d)=\text{True}$
  • $x \sim p_g$ , then $D(x;\theta_d)=\text{False}$
  • 어떠한 근거로 판단하는지는 알 수 없다.
    
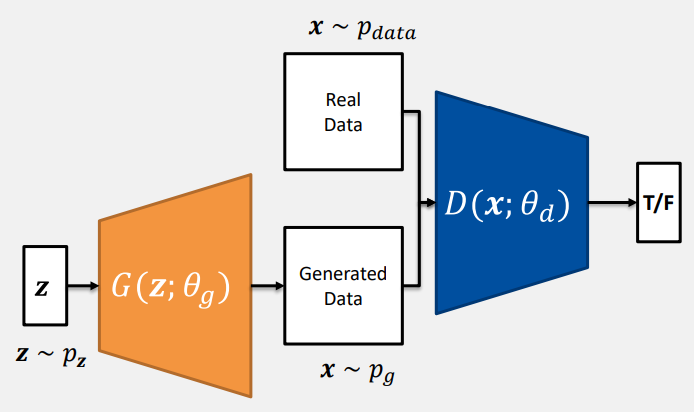
    • $z \sim p_z$: $z$는 자연계 data이므로 일반적으로 정규분포를 따른다.
    • $G(z;\theta_g)$: 입력 $z$로 data를 생성한다. 학습이 진행되면 $\theta_g$가 업데이트된다.
    • $x \sim p_g$: $x$는 network를 거쳐서 생성된 이미지로, G가 만들어낸 확률 분포 $p_g$를 따른다.
    • $x \sim p_{data}$: 실제 이미지 data
    • $D(x;\theta_d)$: data를 입력받아 실제 이미지인지 생성된 이미지인지 판단한다.

The learning objective of D

Goal: random 분포에서의 값으로 generate하면 False라 하는 것이 D의 목표이다.

D 학습 시 G는 freezing, 학습하지 않고 함수로만 사용한다.

• 실제 데이터인 경우, $x \sim p_{data}$, then $D(x;\theta_d)=\text{True}$
  $\max_D \mathbf{E}_{x\sim p_{data}}[\log{D(x)}]$
• 생성된 데이터인 경우, $x \sim p_g$, then $D(x;\theta_d)=\text{False}$
  $\max_D \mathbf{E}_{z \sim p_z}[\log{(1-D(G(z)))}]$

The learning objective of G

Goal: data의 분포를 capturing 할 수 있고 $D(G(z))=\text{True}$가 되도록 학습한다.

G 학습 시 D는 freezing, update 하지 않고 함수로만 사용한다.

• 학습을 진행하며 D의 영향을 받을 수밖에 없다.
  $\min_G \mathbf{E}_{z\sim p_z}[\log{(1-D(G(z)))}]$
• G에 비해 학습이 느려 한 번씩 실제 데이터를 보여주기도 한다.

GAN Loss

• Non-saturating GAN Loss
  • 학습 초기에는 $D(G(z))$의 성능이 좋지 않아 값이 0에 가깝다.

기존의 G 학습 방향	Non-Saturating loss
$1-D(G(z)) \rightarrow 0$	$D(G(z)) \rightarrow 1$
$\min_G \mathbf{E}_{z\sim p_z}[\log{(1-D(G(z)))}]$	$\max_G{\mathbf{E}_{z\sim p_z}\log{D(G(z))}}$
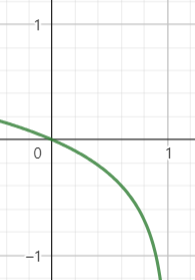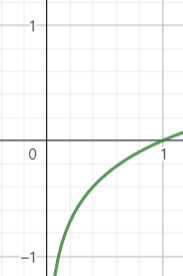학습 초기에 기울기가 거의 없다.	학습 초기에 기울이가 크다.

How GAN is trained

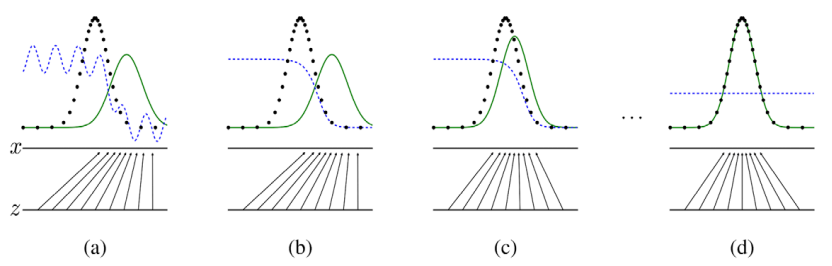
• $x$: $p_z$를 따르는 $z$로부터 생성된 이미지 $G(z)$

1. (a): $x$의 분포가 실제 이미지보다 오른쪽에 치우쳐 있다.
   • $G$는 $z$를 $x$로 mapping하는 함수
   • $D(G(z))$는 실제 분포와 생성된 분포를 평가하는 파란색 점선
   • 검정색 점섬은 Gaussian Distribution을 따르는 실제 이미지
2. (b): $G$ back propagation을 통해 $x$는 왼쪽으로 이동한다.
   • $D$는 실제 분포와 생성된 분포를 구분하여 왼쪽 값은 1, 오른쪽 값은 0으로 반환한다.
3. (c): $\theta_g$가 update 되어 $z$의 분포는 조금씩 왼쪽으로 이동한다.
4. (d): $D$가 더이상 구분하지 못한다.

• $z$의 평균이 실제 데이터의 평균과 동일하고 분산은 더 작다면 overfitting
  • Mode Collapse: Generator가 다양한 이미지를 만들어내지 못하고 비슷한 이미지만 계속 생성하는 문제
  • GAN의 학습 목표, 학습 기준이 다양성에 대한 것이 아니기 때문에 이를 막을 수는 없다. $\rightarrow$ style GAN
• 실제 데이터와 초기 $x$의 분포가 지나치게 떨어져 있다면 $D$의 판단의 기울이가 일정하기 때문에 $G$의 학습 방향을 알 수 없다.
  • 이를 해결하기 위해 $D$에게 answer로 Gauissian 분포와 $G(z)$의 분포를 섞어서 보여준다.

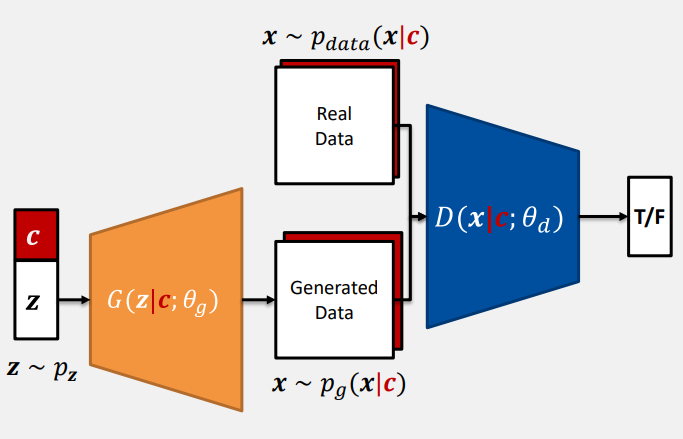
Conditional GAN

• condition을 Generator와 Discriminator에 동일하게 부여한다.
  • Generator: $G(z|c;\theta_g)$
  • Discriminator: $D(x|c;\theta_d)$
  • Real Data: $x \sim p_{data}(x|c)$
  • Generated Data: $x \sim p_g(x|c)$
• Neural network 구조에 따라 $c$의 입력 방식이 달라진다.
  • Linear layer이면 $c$를 입력 vector에 concatenate
  • Convolution layer이면 one-hot encoded $c$를 input image channel에 추가한다.