Convolution Neural Network

‍이세현·2025년 4월 22일

CNN의 등장

Neural Network 이전에 이미지를 처리하기 위해 Histogram of Oriented Gradients (HoG), Bag of Words 활용하여 직접 feature를 추출하여 처리했다. Feature extraction 방법은 최적의 성능이 보장되지 않는 문제가 있다.

CNN: History

LeNet
- 최초의 Convolutional Neural Network인 LeNet은 깊이가 얕고 크기가 작아서, 작은 데이터를 처리하기에 유용하다.
AlexNet
- ILSVRC 2012에서 우승한 AlexNet은 LeNet과 유사하지만 더 깊고 크기가 크며, 유의미한 정규화 (Drop out) 과정이 포함되어 있다.
- 사람이 직접 특징을 추출하는 hand craft feature 시대에서 End-to-End로 처리하여 최적의 파라미터를 구할 수 있는 시대가 열렸다.
- 적었던 데이터는 ImageNet이라는 큰 데이터셋의 등장으로 해결되었고, 과적합과 기울기 소실 문제는 ReLU와 Drop out의 사용으로 해결할 수 있었다. 또한 시간 복잡도 문제는 GPU 사용으로 해결하였다. 이를 통해 CNN의 사용이 활발해졌다.

Convolution Layer

CNN을 구성하는 것으로는 Convolutional layers, Pooling layers, Fully-connected layers, Activation function, Normalization이 있다.

$[32\times32\times3]$ 이미지가 있을 때 필터의 채널 또한 $3$ 이어야 한다. 예) $[5\times5\times3]$
필터와 동일한 크기의 이미지 일부와 필터를 곱하고 bias를 더한다. 예) $[32\times32\times3] \rightarrow [28\times28\times1]$ 크기의 activation map
필터의 개수에 따라 최종적으로 생성되는 activation map의 개수가 결정된다. 예) 필터 개수가 6개이면 $[6\times28\times28]$ 크기의 activation maps
필터 하나 당 scalar인 bias가 하나씩 포함된다.
입력한 이미지의 개수에 따라 출력되는 activation maps 즉, output의 개수가 결정된다. 이는 Batch of images라고 부른다. 예) $2\times3\times32\times32 \rightarrow [2\times6\times28\times28]$
요약하면 $[N\times C_{in}\times H\times W]$ 입력 이미지는 $[C_{out}\times C_{in}\times K_w\times K_h]$ 필터를 거쳐 $[N\times C_{out}\times H'\times W']$ outputs을 생성한다.

Structure of CNNs

$[32\times32\times3]$ 크기의 이미지는 6개의 $[5\times5\times3]$ 필터 연산을 한 후 활성화 함수를 거쳐 $[28\times28\times6]$ 출력을 생성한다. 활성화 함수는 일반적으로 ReLU 함수가 사용되며, linear layer 여러 개로 구성된 Neural Network와 마찬가지로 Conv, Nonlinear와 같이 비선형 함수가 반드시 포함되어야 한다.

Spatial Dimensions

보통 가로와 세로 $H, W$ 가 동일하므로 $N$ 으로 표기한다.
필터의 크기가 $F$ , stride가 $S$ , padding이 $P$ 일 때 출력의 폭, 높이는 다음과 같다.

N'=\frac{N-F+2P}{S}+1

Stride가 1일 때 크기 정보를 유지하기 위해서는 다음이 성립해야 한다. $N=N-F+2P+1\rightarrow P=\frac{F-1}{2}$
- 필터 크기가 3이면 패딩은 1, 5이면 패딩은 2, 7이면 패딩은 3이어야 크기가 유지된다.

이미지가 입력되고 다음 map으로 넘어가면서 한 픽셀을 결정하는 이전 픽셀 크기는 Receptive Fields라고 한다. 이 영역이 넓을수록 한 픽셀을 결정하는 데 더 많은 정보를 활용한 것이므로 더 효율적이다. $L$ 개의 레이어에서 $K$ 크기의 필터를 사용하였다면 receptive field size는 $1+L\times(K-1)$ 이다.

일반적으로 필터의 개수는 2의 자승으로 설정하며, (필터 사이즈, stride, padding)은 다음과 같은 값이 주로 사용된다. $(3,1,1), (5,1,2), (5,2,\cdot), (1,1,0)$

$[1\times1]$ 필터는 각 픽셀에서 Fully-connected layer 연산을 하는 것과 같다. 이때, 공간 정보는 유지되고 채널 크기만 변경된다. 대표적으로 GoogLeNet에서 사용되었다.

뇌의 관점에서 Convolution Layer

입력 이미지가 $[32\times32]$ 인데 출력은 $[28\times28]$ 인 건, 각 뉴런이 입력의 전체를 보는 것이 아니라, $[5\times5]$ 같은 작은 영역(receptive field)만 본다는 것을 의미한다.
이 뉴런은 그 작은 입력에 대해 weight와 bias를 적용한 후 활성화 함수를 통해 출력을 만들며, 모든 뉴런이 동일한 weight, 즉 필터를 공유한다. 다시 말해 convolution은 지역적이고 파라미터를 공유한다.
필터가 여러 개일 때는, 같은 위치를 여러 시각에서 본다는 것을 의미한다. 예를 들어 필터가 5개이면 출력은 $[28\times28\times5]$ 의 3차원 형태가 된다. 같은 입력 위치라도 서로 다른 필터들이 독립적인 시각으로 처리하므로 같은 위치에 대해 5개의 서로 다른 뉴런이 존재하는 것이다. 결국, 여러 필터는 한 영역을 각기 다른 방식으로 인식한다.

이런 방식은 시각 피질의 동작 원리와도 유사하며, CNN이 이미지를 효과적으로 처리할 수 있는 이유이다.

Pooling Layer

Pooling layer는 파라미터가 없고, 채널과는 무관한 레이어로, Receptive field를 늘리는 가장 쉬운 방법이다.

대표적인 방법으로 Max Pooling이 있다. $[2\times2]$ 크기의 레이어를 stride 2로 설정한다면 앞서 본 필터 연산과 동일하게 사이즈를 구할 수 있다. 출력은 $\frac{N-2}{2}+1=\frac{N}{2}$ 가 된다.

Batch Normalization

배치 정규화는 모델을 단순하게 만드는 regularization 기법이다. 입력 이미지들의 평균을 0, 분산을 1로 변형해서 분포를 고르게 한 뒤 학습을 진행하는 것이다. 변형된 이미지들은 가우시안 분포를 따르게 된다.

\hat{x}^{(k)}=\frac{x^{(k)}-E[x^{(k)}]}{\sqrt{Var[x^{(k)}]}}

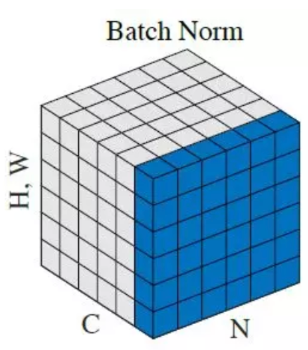
이미지가 $N$ 개 있을 때 차원별로 평균과 분산을 계산하여 정규화할 때 시각화한 그림이다.
보통 정규화 다음으로는 학습 가능한 파라미터 $\gamma, \beta$ 를 정해두고 최종적으로 $y_{i.j}=\gamma_j\hat{x}_{i,j}+\beta_j$ 를 계산한다. 이는, 출력 분포가 항상 고정되어 모델 표현력이 제한되는 것을 방지하는 수단이다.
- $\gamma=\sigma, \beta=\mu$ 가 되게 학습하면 입력 $x$ 가 그대로 나오는 항등 함수가 된다. 이는 BatchNorm의 유연성과 강력함을 보여주는 예시이다. 처음에 분포를 표준화하고, $\gamma, \beta$ 를 통해 원하는 분포로 재조정할 수 있으므로, 모델이 필요하다면 정규화하지 않은 원래 값으로도 되돌릴 수 있다는 뜻이다. 즉, BatchNorm은 모델의 표현력을 해치지 않으면서도 학습을 안정화할 수 있는 안전한 연산이다.
- $N(\mu, \sigma^2) \rightarrow N(0,1) \rightarrow N(\beta, \gamma^2)$
보통 FC layer나 Convolutional layer 다음 단계, 비선형 함수 전 단계에 적용된다.
장점은 다음과 같다.
- Deep networks 학습을 더 쉽게 한다.
- Gradient flow를 향상시킨다.
- 학습률을 높여도 되며, 더 빠르게 수렴한다.
- 초기화 시 networks가 더 견고해진다.
- 학습 중에 정규화, 단순화가 진행된다.

Layer Normalization

Batch Normalization	Layer Normalization
$x:N\times D$	$x:N\times D$
$\mu,\sigma: 1\times D$	$\mu, \sigma: N\times1$
$\gamma, \beta: 1\times D$	$\gamma,\beta:1\times D$
$y=\gamma(x-\mu)/\sigma+\beta$	$y=\gamma(x-\mu)/\sigma+\beta$

Instance Normalization

Batch Normalization	Instance Normalization
$x:N\times C\times H\times W$	$x:N\times C\times H\times W$
$\mu, \sigma: 1\times C\times1\times1$	$\mu, \sigma: N\times C\times1\times1$
$\gamma, \beta: 1\times C\times1\times1$	$\gamma,\beta: 1\times C\times1\times1$
$y=\gamma(x-\mu)/\sigma+\beta$	$y=\gamma(x-\mu)/\sigma+\beta$

ImageNet winners

AlexNet (8 layers)

Conv, Max pool, Norm → Conv, Max pool, Norm → Conv 3 → Conv 4 → Conv 5, Max pool → FC 1 → FC 2 → FC 3

Input: $[227\times227\times3]$
First conv layer: $[96\times11\times11]$ 필터, stride는 4
- Output: $[55\times55\times96]$
- Parameter 개수: $(11\times11\times3+1)\times96$
First max pool layer: $[3\times3]$ 필터, stride는 2
- Output: $[27\times27\times96]$
- Parameter 개수: $0$
활성화 함수는 ReLU, dropout은 0.5 등

ZFNet (8 layers)

AlexNet 일부 미세 조정한 network이다.

VGGNet (19 layers)

VGGNet의 핵심 아이디어는 작은 필터를 여러 층 쌓아 깊은 네트워크를 학습하는 것이다. 오로지 $[3\times3]$ 필터를 사용하고, stride는1, padding은 1이며, $[2\times2]$ Max pool 레이어의 stride는 2이다.
$[3\times3]$ 처럼 작은 필터를 여러 개 쌓으면 receptive field가 늘어난다. 세 개의 $[3\times3]$ 필터를 사용하는 것은 $[7\times7]$ 필터를 사용하는 것과 동일한 효과를 가진다. 정확히 말하면, 파라미터 수도 절감되고 비선형성이 더 추가되어 $[7\times7]$ 필터를 사용하는 것보다 더 효율적이다.

하지만 VGGNet에는 크게 두 가지 단점이 있다.

특히 첫번째 feature size가 너무 크다.
최종 flatten size가 너무 커서 FC 레이어에서 많은 파라미터가 필요하다.

GoogLeNet (22 layers)

GoogLeNet의 핵심 아이디어는 연산 효율성을 챙기면서 네트워크를 깊게 쌓는 것이다. 마지막에 FC layer는 없고 Single linear classification 과정만 있다.

Inception Module
- 한 층 안에서 다양한 필터 크기와 max pooling을 병렬로 적용하는 것을 Network in network라고 한다. 각 필터는 입력의 서로 다른 receptive field를 바라보고, 그 결과들을 channel-wise로 concat해서 하나의 출력으로 만든다. 이와 같이 한 층에서 여러 시야를 병렬로 학습하는 것이 inception module의 핵심이다.
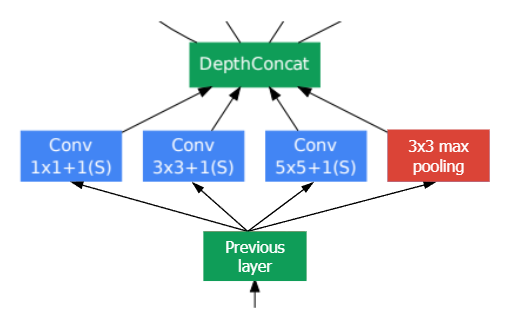
- 위 그림에서 서로 다른 필터 연산을 거치면 출력 사이즈가 다음과 같이 계산된다.
  - 입력 크기 $[28\times28\times256]$
  - $1\times1$ conv → $[28\times28\times128]$
  - $3\times3$ conv → $[28\times28\times192]$
  - $5\times5$ conv → $[28\times28\times96]$
  - $[3\times3]$ max pool → $[28\times28\times256]$
  - Output은 $[28\times28\times672]$
- Feature map 채널 수가 너무 많아지고, 연산량이 너무 많아서 네트워크가 점점 무거워지는 문제가 있다. 또한 pooling 레이어도 공간 크기를 줄이기 위한 연산이지만 concatenation 이후 depth가 유지되는 문제가 있다.
- 이 문제를 해결하기 위해 $[3\times3], [5\times5]$ 처럼 큰 커널에 들어가기 전에 $[1\times1]$ convolution을 먼저 적용하여 채널 수를 줄일 수 있다. 예를 들어 $[1\times1]$ conv로 256차원을 64로 줄인 뒤 $[3\times3]$ conv를 적용하면 연산량을 줄일 수 있다. 이를 Bottleneck Layer라고 한다.
- Bottleneck layer: 계산량은 줄이고, 정보 표현은 유지할 수 있다.
$[1\times1]$ Convolution
- 입력 이미지가 $[56\times56\times64]$ 이고 필터의 개수가 32개라면 출력 크기는 $[56\times56\times32]$ 이다. 이 과정은 각 픽셀 위치마다 64차원 벡터에 Fully Connected Layer를 적용하는 것과 같다.
- 공간 정보는 유지하고 채널 수를 줄이는 것은 연산량과 파라미터 수를 줄이면서도 표현력을 유지하는 것이다.
- 여러 feature map을 조합하여 의미 있는 새로운 feature를 만들 수 있다.
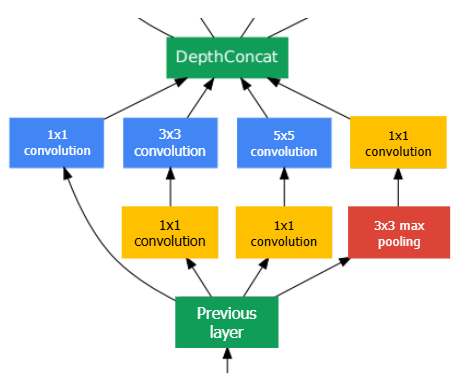
- 위 그림에서는 입력의 채널 수를 줄인 후 복잡한 연산을 수행하여 전체적인 계산량을 줄인다. 가장 오른쪽의 pooling layer에서도 $[1\times1]$ convolution을 붙여서 정보 손실을 줄이고 채널 수를 정돈한다.
GoogLeNet에서 첫번째 단계에서 $[7\times7]$ 필터를 사용하여 feature size를 대폭 줄인다. 이후 Inception Modules 여러개를 사용하여 계산량을 줄이면서도 다양한 수준의 특징을 동시에 학습한다. 마지막 Convolutional 레이어 이후에 FC layer를 사용하지 않고 global average pooling 레이어를 사용하여 공간 정보를 유지한다. 이후 FC layer를 한 층 사용하여 전체적인 파라미터 수를 절감한다.
하지만 Network가 깊어질수록 기울기가 소실되는 문제가 있다. 이를 해결하기 위해 중간에 softmax를 추가한다.

ResNet (152 layers)

ResNet은 residual connections를 활용한 deep networks이다. 단순 convolutional neural network를 여러 층 쌓게 되면 성능이 나빠진다. 하지만 training 단계에서도 성능이 낮아지므로 과적합은 아니다. 따라서 다음과 같은 가설을 세울 수 있다.

모델이 깊어질수록 파라미터가 많아지고 더 강력한 표현력을 가지게 된다.
그렇다면, 모델이 깊어질수록 최적화가 어려운 것은 아닐까?

깊은 모델을 최소한 shallow model의 성능만큼 보장할 수는 없을까? 이에 대한 답변이 바로 shallower model의 출력을 copy하는 것 즉, residual connection이다. 수식으로 표현하면 $H(x)=F(x)+x$ 이다. 이때 $x$ 를 shallower model의 출력이라고 보면 된다.
ResNet이 효율적인 이유를 요약하면 다음과 같다.

최종 성능을 shallow Network의 성능만큼 보장할 수 있다.
$F(x)$ 는 입력된 feature $x$ 가 어떻게 바뀌는지, 얼마나 바뀌어야 하는지 설명한다. $F(x)=H(x)-x$
이전 기울기가 흐르게 되어 기울이 소실 문제를 해결한다.

FC 레이어는 가장 마지막에 클래스를 예측하는 단계에만 있다. 이론적으로 ResNet은 다양한 크기의 입력을 처리할 수 있다.

Networks가 더욱 깊어지면 bottleneck 레이어를 사용하여 효율성을 높일 수 있다. 입력이 들어오면 $[1\times1]$ conv filter를 사용하여 채널 수를 줄이고, $[3\times3]$ conv filter를 거친 후 다시 $[1\times1]$ filter를 사용하여 원래 채널로 되돌리는 방식으로 사용한다.

ResNet 요약 및 실험 설정
- 성능 저하 없이 네트워크를 키울 수 있다.
- 매 conv layer를 거친 후 batch normalization을 적용한다.
- Xavier 초기화 사용
- SGD + Momentum (0.9)
- Learning rate: 0.1, 학습 속도가 낮아지면 단계적으로 10으로 나누어준다.
- 배치 크기 256
- Weight decay $10^{-5}$
- No dropout

Comparing complexity

AlexNet	VGGNet	GoogLeNet	ResNet
적은 연산	가장 많은 연산	적은 연산	꽤 적은 연산
낮은 정확도	꽤 높은 정확도	꽤 높은 정확도	높은 정확도

Training Neural Networks

Activation Functions

Sigmoid function $\sigma(x)=\frac{1}{1+e^{-x}}$ 은 $x$ 가 0에 가까울수록 기울기가 크지만 $-\infin$ 또는 $\infin$ 으로 갈수록 기울기가 0으로 수렴한다. 이러한 이유로, 대부분의 경우 weight가 업데이트되지 않는다.

$\tanh(x)$ 함수는 함수값의 범위가 $[-1,1]$ 로 정렬되었지만 마찬가지로 대부분의 경우 gradient가 0이 된다.

반면 ReLU function은 $x>0$ 영역에서 기울기가 0으로 수렴하지 않아 수렴이 빠르고 연산이 효율적이지만, 반대 영역에서는 여전히 gradient가 0인 문제가 있다. 그리고 $x=0$ 일 때에는 기울기가 없다.

이런 ReLU의 문제를 해결하고자, 0보다 작을 때에는 작은 기울기를 넣어주는 방법이 LeakyReLU이다. ReLU의 장점은 모두 가져가면서, 단점은 모두 해결한 함수이다. 음수 영역에서 기울기 $\alpha$ 는 학습 가능한 파라미터이다.

이와 같이 사용되는 방법이 Exponential Linear Units(ELU)이다. ReLU의 모든 장점은 그대로 가져가지만 음수일 때에는 $\alpha(\exp(x)-1)$ 을 계산해야 해서 연산량이 조금 더 높다.

ReLU에 Dropout 방식을 더한 Gaussian Error Linear Units(GELU) 방식도 있다.

Weight Initialization

모델을 학습할 때 가장 처음 가중치 값을 0으로 설정하면, 기울기가 항상 0이기 때문에 학습이 진행되지 않는다.

Small random numbers

W=0.01\times\text{np.random.randn}(D,H)

이 방식은 작은 모델에서는 효율적이지만, 네트워크가 깊어질수록 문제가 된다. 네트워크가 깊다면 뒤의 레이어로 갈수록 활성 함수에 입력되는 값이 0에 수렴하게 된다. 기울기 또한 0에 수렴하여 학습할 수 없는 상태에 도달하게 된다.

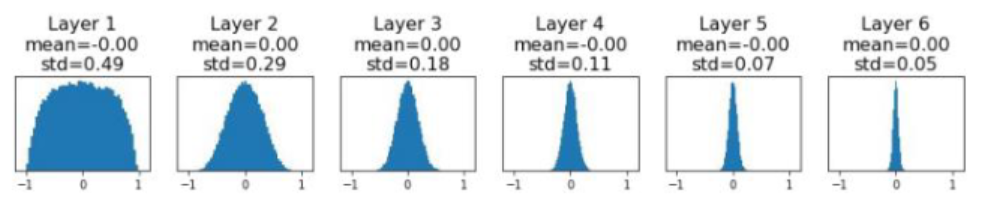
$0.01$ 을 $0.05$ 로 키우더라도 local gradients는 0이기 때문에 더이상 학습할 수 없는 상태에 도달하게 된다.

Xavier Initialization

\frac{\text{np.random.randn(D,H)}}{\sqrt{D}}

표준정규분포 $N(0,1)$ 를 따르는 값을 입력 차원의 제곱근으로 나누는 방법이다. 활성화 함수를 거치면 모든 레이어에서 적절하게 값이 분포된다.

$w_i$ 의 분산이 $\frac{1}{D}$ 가 되고, 입력 값 $x_i$ 의 분산과 $y$ 의 분포는 같아진다.

활성화 함수가 ReLU 함수라면 분포는 다음과 같이 변한다.

‍이세현

Hi, there 👋

이전 포스트

Linear Regression

다음 포스트