Longitudinal Controls

Longitudinal Control Overview

종방향 제어란 차량의 앞뒤 방향 움직임을 제어하는 것으로, 종방향 속도, 가속도, 앞선 차량과의 간격 조절이 이에 해당한다.

Standard Cruise Control은 오늘날 대부분의 자동차에서 이용 가능한 대표적인 종방향 제어 시스템이다. 운전자가 원하는 속도를 설정하면 cruise control system이 자동으로 스로틀을 조절하여 속도를 유지한다.

종방향 ADAS 시스템의 예로 다음과 같은 것들이 있다.

• Cruise Control: 일정한 속도를 유지하는 시스템이다.
• Adaptive Cruise Control: 정속으로 주행하다가 속도가 느린 전방 차량과 가까워지면 라이다(radar)로 감지하여 속도를 조절하고, 거리를 유지한다. 전방 차량이 다른 차선으로 옮기면 속도를 조절한다.
• Stop & Go: 정지 후 다시 출발까지 자동으로 수행하는 시스템이다.
• Collision Avoidance: 앞선 차량과의 간격 유지가 어렵다고 판단되면 경고를 울리거나 자동으로 감속한다.
• Automated Highway System: 고속도로에서 차량들이 좁근 간격을 두고 주행할 수 있어 교통 흐름 개선에 도움이 된다.

이러한 시스템은 차량의 센서를 기반으로 차량의 상태를 측정하고, 제어기가 속도, 거리, 가속도를 조절해주는 방식으로 작동한다.

Cruise Control

Cruise Control System Overview

Cruise Control System은 고속도로에서 유용한 기능으로, 버튼으로 켜고 끌 수 있으며, 사용자의 페달 입력이 발생하면 종료된다.

• 측정값: Ego 차량의 현재 속도
• 조작값: 스로틀(엔진에 들어가는 공기양), 브레이크 패달은 조절하지 않는다.
• 제어 목표: 설정한 속도를 정상 상태 오차 없이 유지하는 것
  • 정상상태 오차는 안전과 직결되므로 운전자에 의해 결정된 지정 속도를 정상상태 오차 없이 추종하는 것이 중요하다.

Controller 구조

Cruise Control System은 두 개의 제어기 계층으로 나눌 수 있다.

1. Upper Controller
   • 입력: 설정 속도, 현재 차량 속도
   • 출력: 차량이 따라야 할 목표 가속도
2. Lower Controller
   • 입력: 상위 제어기가 만든 목표 가속도
   • 출력: 스로틀 밸브를 조절해서 실제 차량을 가속하거나 감속

Upper Controller

상위 제어기는 설정한 속도와 현재 속도의 차이를 기반으로 하위 제어기에 전달할 가속 신호를 생성한다. 실제 차량은 가속 페달을 밟는다고 해서 즉시 속도가 올라가지 않고 무게 등 여러 요인으로 인해 천천히 변화한다. 이러한 상위 제어기는 간단한 1차 지연 함수로 모델링할 수 있다.

• $\tau$: 시스템이 반응하는 속도(시정수, 보통 0.5~1초로 설정), 지연 정도를 나타내는 상수이다.
• $s$: 시간 도메인을 주파수로 바꾸는 변수

이 모델은 운전자가 어떤 입력을 주면, 차량은 바로 반응하지 않고 지연되는 것을 수학적으로 표현한 것이다.

• 입력이 1(True)로 바뀌고 시간이 $\tau$일 때 출력은 입력의 약 63%에 도달한다. $\tau$를 1로 결정할 경우 1초 뒤 약 63%의 지연이 발생한다. 시간이 $3\tau$일 때 출력은 입력의 95%에 도달한다. 이걸 지연된 추종이라고 부른다.

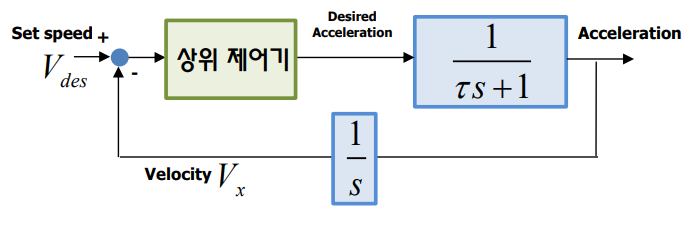
설정한 목표 속도 $V_{des}$에 따라 상위 제어기가 목표 가속도를 계산하면 지연함수에 의해 실제 속도가 변화한다.

실제 가속 값은 다음과 같이 계산된다.

상위 제어기는 속도 오차 $e(t)$를 보고 차량이 어느 정도 가속해야 하는지 결정한다. 하지만 지연이 발생하게 되면 단순한 비례 제어만으로는 오차가 남을 수 있다. 따라서 PD 제어, PI 제어를 통해 오차를 빠르게 줄여야 한다.

• PD 제어 $K_P+K_DS$
  Proportional 제어는 오차가 클수록 더 크게 조절하는 제어, Derivative 제어는 오차의 변화량에 반응하여 예측 조절하는 제어이다.
  • 속도 오차 $e(t)=V_{dex}-V_x$
  • $\ddot{x}_{des}(t)=k_p\cdot e+k_d\cdot\dot{e}$
  • 오르막, 또는 내리막에서 PD제어는 큰 도움이 되지 않는다. 제어를 통해 안정 상태에 도달하여도 error가 지속되는 경우에는 $k_p$를 키우거나 다른 feedforward term을 추가하여 해결할 수 있다.
• PI 제어 $K_P+K_I/S$
  • Integral 제어는 누적된 오차를 없애기 위해 천천히 조절하는 제어이다.
  • $\ddot{x}_{des}(t)=-k_pe(t)-k_I\int_0^te(t)dt$
  • $\ddot{x}_{des}(t)=-k_p(\dot{x}-\dot{x}_{des})-k_I(x-x_{des})$
  • I term은 오차가 누적되어 시스템이 발산하는 문제로 이어질 수 있다.

Lower Controller

하위 제어기는 상위 제어기로부터 전달받은 목표 가속도를 입력으로 하여, 실제 차량의 가속도가 원하는 값이 되도록 스로틀(엔진 토크)을 조절한다. 하위 제어기에는 다음과 같은 가정이 앞선다.

• 자동 변속할 때 사용하는 장치인 토크 컨버터는 Lock-up 된 상태이다. 순항 제어 기능은 보통 고속 주행 시 사용하기 때문이다.
• 타이어와 노면에서 생기는 타이어 슬립의 크기는 0이다.

하위 제어기는 차량 종방향 운동, 파워트레인 모델을 이용하여 설계된다. 목표 가속도를 받고, 운동 방정식을 바탕으로 필요한 엔진 토크를 계산한 뒤, 그 토크를 만들어내기 위한 스로틀 각도를 계산하여, 액추에이터를 작동시켜 차량을 실제고 가속시킨다.

• Vehicle Longitudinal Dynamics
  $m\ddot{x}=F_{xf}-F_{aero}-R_{xf}-R_{xr}-mg\sin\theta$
• Powertrain Model
  • 바퀴의 각속도는 엔진의 각속도에 비례하므로 $\omega_w=R\cdot\omega_e$가 성립하고 $\omega_e=\omega_t$로 엔진과 변속기 속도와 동일하다.
  • 유효 바퀴 반지름이 $r_{eff}$일 때 차량의 속도 $\dot{x}=V_x=r_{eff}\cdot\omega_w$
  • 가속도 $\ddot{x}=r_{eff}\cdot R\cdot\dot{\omega}_e$

• Wheel Dynamics
  • 바퀴의 관성 모멘트가 $I_w$이고 바퀴에 전달된 토크가 $T_\text{wheel}$일 때 $I_w\dot{\omega}_w=T_\text{wheel}-r_{eff}F_{xf}$가 성립한다. (앞서 구한 $F_{xf}$로 대입 가능)

Adaptive Cruise Control

적응형 순항 제어

ACC는 크루즈 컨트롤의 발전된 제어 시스템이다. 크루즈 컨트롤은 설정한 속도를 일정하게 유지하고, 앞차가 생겨도 무시하기 때문에 운전자가 브레이크를 수동으로 밟아야 한다. 반면에, 적응형 크루즈 컨트롤은 가속 페달과 브레이크 페달을 사용하지 않고, 운전자가 설정한 속도로 자동 주행을 하다가 차량 전면부의 레이다 센서 등을 사용하여 전방 차량이 감지되면 전방 차량과의 거리를 자동으로 유지할 수 있다.

ACC의 시스템

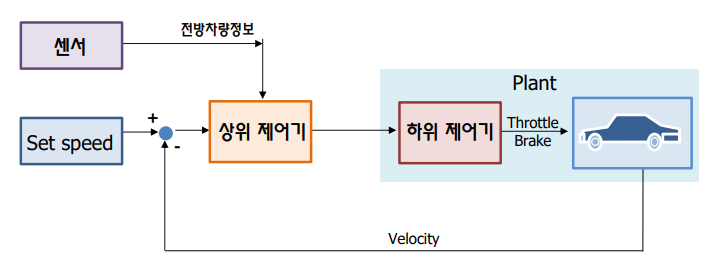
전방에 차량이 존재하지 않을 경우 지정된 속력을 제어하고, 전방에 차량이 존재할 경우 전방 차량과의 거리를 유지하며 추종 제어해야 한다.
ACC를 구성하는 시스템은 크게 센서, 액추에이터, 제어기가 있다.

• 센서: 휠 속도 센서, 브레이크 페달 센서, 스로틀 페달 센서, 레이다 등의 센서로 차량 간 상대 거리 및 상대 속도 등 필요한 값을 모두 측정할 수 있다고 가정한다.
• 액추에이터: 브레이크 및 스로틀 엑추에이터
• 제어기: 상위 제어기와 하위 제어기

ACC의 안정성 요구 조건

ACC의 stability(안정성)으로는 크게 두 가지가 있다. "Ego 차량" 자체의 안정성과 여러 대의 차량이 줄지어 주행하는 "군집 차량들" 안정성.

Individual Stability

개별 안정성을 나타내며, 자차량 안전 조건을 뜻한다. 한 대 한 대 안정적으로 따라가는 것을 만족하면 individual stability를 만족한다.

• 전방 차량의 가속도가 0일 때 거리 오차가 0이 될 수 있는지에 대한 기능적 여부 $\text{If }\ddot{x}_{i-1}\rightarrow0, \text{THEN }\delta_i\rightarrow0$
• 거리 오차$(\delta)$는 유지하고 싶은 간격 $L_\text{des}$와 실제 간격의 차이를 의미한다. $\delta_i=L_\text{des}-(x_{i-1}-x_i)$
• $\delta_i$를 미분하면 $\ddot{\delta}_i=\ddot{x}_i-\ddot{x}_{i-1}$

String Stability

ACC 기능을 수행하는 여러 대의 차량 대열에서, 각 차량 가나 인지, 제어 등 시간 지연에 따른 차량 간의 거리 오차 증폭을 방지하기 위한 조건을 뜻한다.

• 오차 값이 증폭될 경우, 뒤따라 주행하는 차량 간의 사고를 유발할 수 있다. 이러한 이유로, Individual stability를 만족하더라도 String stability는 만족하지 않을 수 있다.
• 거리 오차 전달 함수의 크기는 1보다 작아야 한다. 전달함수의 크기가 1보다 크면 전달함수 간 곱셈에 의해 거리오차가 증폭될 가능성이 있기 때문이다.
  $\hat{H}(s)=\frac{\delta_i}{\delta_{i-1}}, \quad \|\hat{H}(s)\|<1\quad\therefore\|\delta_i\|_2\le\|\delta_{i-1}\|_2$
• Impulse 입력에 대한 거리 오차의 부호는 동일해야 한다.
  • 예를 들어 $i$번째, $i+1$번째 차량이 $\delta_{i+1}<0$ 상태에서 거리 오차를 줄이기 위해 $i+1$ 차량이 가속하고, $\delta_{i}>0$ 상태에서 가장 앞서가는 $i-1$번째 차량과 간격을 키우기 위해 $i$번째 차량이 감속한다면 $i,i+1$ 차량 간 충돌이 발생한다.

ACC 제어 시스템을 통해 운전 주행 안정성을 개선하고 운전으로 인한 피로를 줄일 수 있다. 또한 운전자의 부주의에 의한 사고를 줄일 수 있다.

Upper Controller

전방 차량과 일정 거리를 유지하거나 전방 차량과 상대 속도를 유지하는 방식으로 설계할 수 있다.

• Constant Spacing Policy: 전방 차량과 제어 차량의 상대 거리를 항상 일정하게 유지
  • 전방 차량과 유지해야하는 거리 $L_\text{des}$는 상수이다.
  • 가속도를 PD 제어 입력으로 단순화했을 때 $\ddot{x}_i=-k_p\delta_i-k_d\dot\delta_i$
  • 거리 오차 $\delta$는 현재 전방 차량과의 간격, 그리고 목표 간격의 오차이므로 $x_i-x_{i-1}+L_\text{des}$로 계산된다.
    $\ddot{\delta}_i=\ddot{x}_i-\ddot{x}_{i-1}=(-k_p\delta_i-k_d\dot\delta_i)-(-k_p\delta_{i-1}-k_d\dot\delta_{i-1})$
  • 라플라스 변환을 거치면 아래의 전달함수가 정의된다.
    $\frac{\delta_i}{\delta_{i-1}} = \frac{k_ds+k_p}{s^2+k_ds+k_p}=\frac{k_p}{s^2+k_ds+k_p}\cdot\Big(\frac{k_d}{k_p}s+1\Big)=G_1(s)\cdot G_2(s)$
  • String Stability를 만족하기 위해서는 $\|H(s)\|_\infin<1$을 만족해야 한다. 즉, 어떤 주파수에서도 앞차의 신호가 ego 차량에서 더 커지지 않아야 한다. 전달 함수를 분해하면 $G_1\cdot G_2$로 표현할 수 있다.
    • $G_1$은 감쇠 조건으로, $\frac{k_d}{2\sqrt{k_p}}\ge0.707, \quad k_d\ge1.414\sqrt{k_p}$을 만족해야 1보다 작아진다.
    • $G_2$는 제로 영향 조건으로, $\sqrt{k_p}>k_d$를 만족해야 1보다 작다.
    • 즉, $k_d$는 충분히 커야 하지만 너무 크면 안 되는 모순이 발생한다. 결론적으로 constant spacing policy는 individual stability는 만족할 수 있지만 string stability는 만족할 수 없기 때문에 ACC에 부적합하다.
• Constant Time-gap Policy: 전방 차량과 제어 차량 간의 상대 거리를 시간으로 환산하여 일정 시간 차이를 둘 수 있도록 제어
  • 희망 유지 거리를 자차량의 속도에 비례하도록 설정한다. 앞 차의 길이가 $l_{i-1}$일 때 유지하고 싶은 거리 $L_\text{des}$는 $l_{i-1}+h\dot{x}_i$로 표현된다. 해석하면, 자차의 속도가 빠를수록 더 멀리 떨어져야 안전하다는 것을 의미한다고 볼 수 있다.
  • 거리 오차 $\delta$는 $L_\text{des}-(x_{i-1}-x_i)$이므로 전개하면 $x_i-x_{i-1}+h\dot{x}_i$로 표현할 수 있다.
  • 제어의 목적은 희망 유지 거리 $L_\text{des}$와 현재 거리의 오차 $\delta$를 0으로 수렴시키는 것이다. 미분 방정식을 이용하여 $\dot{\delta}_i=-\lambda\delta_i$와 같이 표현된다.
  • CS 정책과 마찬가지로 PD 제어기에서 제어 입력은 $u_i=\ddot{x}_i=-k_p\delta_i-k_d\dot{\delta}_i$이므로 $\dot\delta_i=\dot{\epsilon}_i+h(-k_p\delta_i-k_d\dot\delta_i)$이다. 하지만 앞서 구한 $\dot{\delta}_i=-\lambda\delta_i$와는 등식이 성립하지 않으므로 단순 PD 제어기는 CTG ACC 전략에 적합하지 않다. CTG는 속도에 따라 오차 정의가 달라지고, 이것이 다시 오차 미분에 영향을 주기 때문에 오차를 제대로 0으로 수렴시키기 어렵다. 따라서 제어 목적을 달성하기 위해 설계한 제어기는 거리 오차와 상대 거리 두 항을 동시에 이용한다.
    $u_i=\ddot{x}_i=-\frac{1}{h}(\epsilon_i+\lambda\delta_i)$
    • 위 식은 상대 속도 $\dot\epsilon_i$ 항을 소거하기 위해 $k_d=\frac{1}{h}$로 설정하여 유도한 것이다.
    • 시간 지연 함수에 따라 계산하면 전달함수가 도출된다.
      $\hat{H}(s)=\frac{\delta_i(s)}{\delta_{i-1}(s)}=\frac{s+\lambda}{h\tau s^3+hs^2+(1+\lambda h)s+\lambda}$
    • 이 전달함수가 모든 주파수 영역에서 1보다 작으려면 $h\ge2\tau$를 만족해야 한다.

Range-Range Rate 기반 제어기 설계

ACC 주행 중에 상황이 급변할 때 속도 제어에서 거리 제어 모드로 전환하는 Transitional Control이 필요하다. 전환 제어 설계에서 중요한 것은 승차감과 안전성이 중요하다. 앞차가 갑자기 생겼을 때 속도로 제어할 것인지, 거리 제어로 전환할 것인지, 충돌 회피를 위해 급제동할 것인지 결정해야 한다. 이 판단을 거리와 상대 속도 다이어그램을 기반으로 결정한다.

앞차와의 거리 $R$, 상대 속도 $\dot{R}=v_p-v$일 때 상대 감속이 일정하다고 한다면 다음이 성립한다.

이때 $C$는 감속량으로, 상수이다. 시간에 대해 적분하면 $\dot{R}(t)=\dot{R}_0+Ct, \R(t)=R_0+\dot{R}_0t+\frac{1}{2}Ct^2$이고 여기서 시간 $t$를 제거하면 다음 식이 유도된다.

$R$과 $\dot{R}$ 사이에 제곱 관계가 존재하고, 이를 통해 $R-\dot{R}$ 다이어그램을 구성할 수 있다.

• 
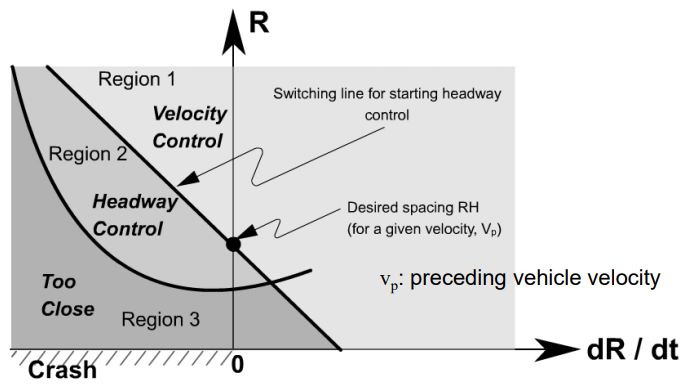
• 앞 차와 거리가 길거나 앞에서 빠르게 가서 상대 속도가 크다면 속도 제어를 유지하고, 이에 비해 가깝거나 앞에서 천천히 간다면 거리로 제어한다.
  • 지나치게 가깝거나 앞에서 느리게 간다면 충돌이 발생할 가능성이 크기 때문에 즉시 제동이 필요하다.

Car-Following Model

Car Following Theory

동일 차로 주행 시 뒷 차가 앞차의 주행 상태에 따라 적절하게 추종하는지에 대해 설명하는 이론이 차량 추종 이론이다. 일반적으로 ACC, 교통 흐름 시뮬레이션 등에 쓰이는데, 차량 간 간격을 유지하거나 string stability 평가 등에 필요하다.

(현실 반영도가 높아 자율주행에서도 자주 쓰인다.)

Intelligent Driver Model

안정적인 가감속으로 최소 안전 거리를 유지하면서 설정된 거리를 유지하고 주행할 수 있도록 고안된 차량 추종 모델로, 연속적이고 정확하면서 간단하기 때문에 차량추종 모형에 오랫동안 사용되었다.

Anti-lock Brake System

ABS란 급제동 시 바퀴가 멈추는 걸 방지해서 차량이 미끄러지지 않고, 제동 중에도 조향할 수 있게 해주는 시스템이다. 바퀴가 잠기면 다음과 같은 문제가 발생할 수 있다.

• 바퀴가 굴러가야 핸들이 돌아갈 수 있다. 바퀴가 잠기면 조향이 불가능해진다.
• 바퀴가 미끄러지면 제동 거리가 증가한다.
• 차가 직선으로만 밀리고, 앞의 장애물을 회피할 수 없어 안전성이 떨어진다.

ABS는 바퀴가 잠기기 직전 상태를 유지하게 한다. ABS의 목표는 다음과 같다.

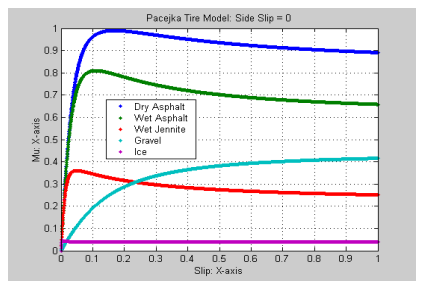
• 타이어가 지면과 접촉할 때, 적절한 슬립율 Slip ratio를 유지하면
• 종방향 마찰력(제동력)도 최대로 유지되고
• 횡방향 마찰력(조향력)도 유지할 수 있다.
  이때, 슬립율은 0.1~0.2 사이의 값이 이상적이다.

하지만, 노면마다 서로 다른 최적의 slip을 찾아야 하고 노면 형태를 예측하기 어렵기 때문에 ABS는 고난이도의 시스템이다. 또한 휠의 속도는 측정할 수 있지만 차량의 속도는 파악할 수 없고 브레이크 압력을 측정할 수 없기 때문에 slip을 측정하기 어렵고, 최적의 slip을 찾는 것은 더욱 어렵다.

ABS 구성 요소

하드웨어 구성은 다음과 같다.

• Wheel speed sensor: 각 바퀴의 회전 속도를 측정한다.
• Hydraulic actuator: 브레이크 압력을 조절하는 디지털 밸브
• Control unit: 제어 로직을 실행한다.

ABS 동작

ABS는 바퀴가 잠기려고 하면 브레이크 압력을 줄이고, 다시 굴러가기 시작하면 브레이크 압력을 다시 높이는 걸 수 밀리초 단위로 반복한다. 브레이크 압력은 3가지 밸브 동작으로 조절할 수 있다.

• Apply: 압력을 유지한다. 평상시에는 열려 있는 밸브이다.
• Dump: 압력을 해제한다.
• Hold: 압력을 유지한다.

바퀴가 잠길 것 같을 때 Apply 밸브를 닫고, 과도하게 전달된 압력은 accumulator에 저장된다.

Conventional ABS

Conventional ABS는 규칙 기반 제어 방식으로, 다음과 같이 특징이 있다.

• 바퀴 회전 속도, 감속도, 슬립율 등을 지속적으로 감지하고 슬립율이나 감속도가 기준치를 넘으면 밸브를 조절한다.
  • 브레이크 압력을 줄이고, 바퀴 회전이 다시 시작되면 압력을 높인다. 이처럼 apply, dump, hold를 디지털 밸브로 짧은 시간 안에 빠르게 반복하면서 바퀴가 잠기지 않도록 한다.
• if / then 방식의 단순한 로직으로, 경제적이고 안정적이지만, 최적의 성능은 아니다.
• 바퀴 회전 속도, 감속도, 밸브 열림 유무 정보를 기반으로 "바퀴가 급하게 느려지면 압력을 줄이고, 바퀴가 다시 굴러가면 압력을 다시 올린다."

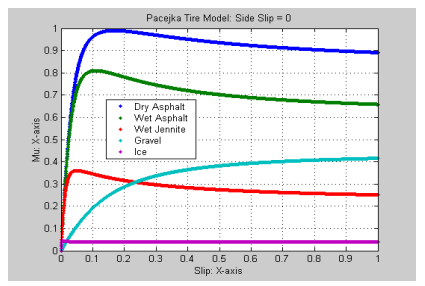
Conventional ABS가 잘 작동하려면 노면 마찰력 $\mu$에 따라 슬립율을 맞추어야 한다. 하지만 현실에서는 노면이 매우 다양하다. (마른 도로, 눈길, 자갈길, 빙판길, 왼쪽 바퀴만 미끄러운 상황 등) 그래서 정확한 마찰 계수나 최적 슬립율을 알기 어렵다. 결국 규칙 기반 방식은 보수적으로 설계될 수밖에 없다.

전통적인 방식의 ABS는 정확한 차량 속도를 측정하기 어렵고, 노면 상태를 알 수 없고, 반복된 apply/dump로 과도하게 유압이 소모되는 문제점이 있다.

Traction Control System

미끄러운 노면에서 바퀴가 헛돌지 않도록 제어해서 안정적인 가속과 주행이 가능하도록 하는 시스템을 TCS라고 한다. 가속 중에 바퀴가 헛돌아 엔진 토크가 과도해지는 것이 감지되면 TCS는 브레이크 압력을 조절한다. 바퀴 속도를 줄이는 이 과정은 다시 힘을 얻게 되어 구동력과 안정성이 높아진다.

바퀴가 헛돌면 다음과 같은 문제가 발생할 수 있다.

• RWD 차량은 뒷바퀴가 미끄러져서 차량이 돌게 된다.
• FWD 차량은 앞바퀴가 헛돌게 되면 핸들 조향이 불가능해진다.
• 4WD 차량은 뒷바퀴가 미끄러지고, 앞바퀴가 헛돌아서 전체적으로 불안정해진다.

구동력이 지면에 전달되지 않으면 가속도 안 되고 조향도 안 된다.

동작 원리

바퀴가 헛돌면 그 바퀴에 브레이크를 살짝 작동한다. 그러면, 반대편 바퀴에 더 많은 토크가 분배되어 전체 차량이 안정적으로 움직이게 된다. 바퀴가 헛돌지 않도록 하기 위해 크게 두 가지 방식으로 제어한다.

1. Engine torque reduction
   바퀴가 헛도는 원인은 엔진이 바퀴에 너무 큰 힘을 전달하기 때문이다. 이럴 때 TCS는 엔진이 바퀴에 주는 힘을 줄여서 바퀴가 헛돌지 않도록 조절한다. 이를 위해 사용하는 대표적인 방법은 다음과 같다.
   • 스로틀 각도 제어: 가속 페달을 밟아도, 전자식 스로틀을 이용해 엔진에 들어가는 공기량을 줄여서 엔진 출력을 줄이고 바퀴에 더 적은 힘을 전달한다.
   • 점화 타이밍 조절: 연료에 불꽃을 점화하는 시점을 늦추어 엔진 출력을 줄이고 엔진 반응을 빠르게 줄인다.
   • 연료 컷: 연료 공급을 일시적으로 차단하여 엔진 토크를 거의 없애버린다. 다만, 이 방식은 배출가스 문제가 생기기 쉽게 때문에 자주 쓰이지는 않는다.
     이 방식은 브레이크 제어보다 느리다. 또한 PD 제어에서 $K_P$보다 $K_D$ 성분이 안정성에 더 도움이 된다.
2. Brake control
   가속할 때 한쪽 바퀴만 헛도는 경우가 많은데, 이럴 때에는 해당 바퀴에만 브레이크를 살짝 걸어 헛도는 바퀴를 늦추고, 정상적인 바퀴로 토크를 보내주는 방식이다. 이런 브레이크 제어는 노면 마찰 계수가 좌우 바퀴마다 다른 split-$\mu$ 상황에서 효과적이다. 예를 들어 한쪽 바퀴가 눈밭에 빠졌을 때 TCS는 그 바퀴에 브레이크를 걸고, 접지력이 좋은 쪽 바퀴로 토크를 옮겨 안정적인 주행을 유도한다.
   이 방식은 Advanced ABS와 유사하게 연속 슬립 제어를 사용한다.

이러한 작동 방식은 ABS와 유사한 점이 있다.

• 제어 목적: 마찰력을 최대로 활용한다.
• 속도 측정: 차량 속도는 모르고 바퀴의 속도만 측정한다.
• 제어 방식: apply/dump 방식을 공유한다. 유압 밸브를 적용한다.
• 사용 센서: 4WD의 경우 가속도 센서로 휠 속도를 측정한다.

반면, 다음과 같은 차이점이 있다.

• 압력 생성: 펌프로 직접 제어
• 속도 인식: 2WD는 차량 속도를 알 수 있다.
• 제어 입력: 엔진 토크와 브레이크
• 요구 성능: 저속에서도 민감한 제어를 요구한다. (언덕길 정지 후 출발 등)
• 기타: TCS는 수동으로 해제할 수 있고, 마찰이 작은 노면에 특화되어 있다.

제어 시 고려 사항

• 부드러움과 최대 접지력 모두 만족해야 한다.
• 정지 상태에서 출발하거나, 도로 마찰 $\mu$가 변화하는 상황, 언덕 주행 상황에서 즉각적인 반응이 필요하다.
• 바퀴가 뒤로 돌면 감지하기 어렵다.
• 주차하거나 저속으로 회전할 때에는 바퀴의 속도가 모둗 달라 오작동 가능성이 있다.

TCS 정리

좋은 Traction Control은 부드럽지만 가속이 충분하고, 반응이 빠르고, split $\mu$ 언덕에서도 밀리지 않고 올라간다.

4WD 차량은 다음과 같은 어려움이 있다.

• 차량 절대 속도를 측정할 수 없다.
• 가속도계 등 추가 장치를 사용하여 센서 보정이 필요하다.
• 다양한 상황에서 튜닝이 필요하다.