Convolutional Neural Networks

Convolutional Network

• Linear Classifier의 한계: 이미지의 공간적 특성을 고려하지 않는다.
  • 이미지 연산에 알맞는 연산이 필요하다.
  • Fully-Connected Network의 구성요소: Fully-Connected Layers, Activation Function
• Convolutional Network의 구성요소: Fully-Connected Layers, Activation Function, Convolution Layers, Pooling Layers, Normalization
  • Fully-Connected Layer: $[32\times32\times3]$ image를 $[3072\times1]$로 펼친다.
    • Weights: $[10\times3072]$, Output: $[10\times1]$
• Convolution Layer: 공간적 구조를 유지한다.

Convolution Layer

Filter

• Filter: 3 채널의 filter로 1회 연산하면 모든 채널을 검사하므로 r, g, b 각각의 연산하여 더한 결과가 나온다. 따라서 연산을 위해서는 filter의 두께를 입력 이미지와 동일하게 설정해야 한다.
• Filter를 image 위에서 딱 한 번 포개어 연산하면 scalar 하나가 도출된다. 3 채널 filter로 1회 연산하면 1 채널 map이 출력된다.
  • $[3\times5\times5]$ filter와 연산하는 것은 75 크기의 벡터와 내적하는 것과 같다.
• Filter의 개수는 출력 map의 채널과 같다.
  • $[C_{in}\times H\times W]$ image, $[C_{out}\times C_{in}\times K_w\times K_h]$ filter $\rightarrow [C_{out}\times H'\times W']$
  • CNN model은 $[C_{out}\times C_{in}\times K_w\times K_h]$ 크기의 filter와 bias이다.
• CNN Filter를 펼치면 vector 내적과 같으므로 linear 연산이다. 따라서 결합벅칙이 성립되고 Convolution Layers를 연속으로 쌓아도 선형성이 있으므로 activation function이 필요하다.
• Filter Size가 이미지만큼 크면 linear classifier의 template matching과 동일하다.
  • Filter는 한 번에 국소적 정보만 훑는다.
  • Kernel size가 1이면 채널 정보는 계산되지만 공간 정보가 담기지 않는다.
    • size 1의 kernel은 채널 크기를 바꾸기 위해 사용한다.

Stride

• Stride: 한 스텝 이후 filter의 이동 pixel

Operations

• Dimension
  $\text{Output}: \frac{(W-K+2P)}{S}+1$
• Receptive Fields
  • $[3\times3]$ 크기의 filter를 사용할 때 하나의 output pixel을 총 9개의 정보로 결정된다. 이때 receptive field는 $[3\times3]$이다.
  • $L$ 개의 레이어에서 $K$ 크기의 필터를 적용했을 때 receptive fields는 $1+L\times(K-1)$
  • 이미지가 작아지면 receptive field가 커진다.
    • 넓은 영역을 보기 위해 이미지 사이즈를 줄이기도 한다.
• Hyperparameters
  • Kernel Size
  • Stride
  • Pooling function

Pooling Layers

Downsample을 위한 방법

Max Pooling

• Information size를 축소하는 방법
• Convolution과 달리 filter 값, parameter가 없다.
• Kernel size, stride에 따라 각 영역마다 최댓값만을 선택하여 다음 convolution에 전달하는 연산
• cf) Average Pooling
• Classic architecture: [Conv, ReLU, Pool] N회, flatten, [FC, ReLU] N회, FC
  • Convolution이 계속되면 공간적 크기는 작아지고 채널은 증가하여 전체적인 볼륨은 보존된다.

Batch normalization

입력 이미지 형태가 다르면 gradient가 매우 다르므로 input data의 range 규제가 필요하다.

Example

• $N$개의 데이터 각각은 $D$ 차원이다.
• 차원(채널)별 평균 $D$개: $\mu_j=\frac{1}{N}\sum_{i=1}^{N}x_{i,j}$
• 차원(채널)별 표준편차 $D$개: $\sigma_j^2=\frac{1}{N}\sum_{i=1}^{N}(x_{i,j}-\mu_j)^2$
• 미세 조정된 $x$: $\hat{x}_{i,j}=\frac{x_{i,j}-\mu_j}{\sqrt{\sigma_j^2+\epsilon}}$
• 문제점
  • Test set의 평균과 표준편차를 구할 수 없다.
    • Train set의 $\mu, \sigma$를 사용한다.
  • 데이터의 평균을 0으로 맞추고, 분산을 1로 맞추는 엄격한 정규화가 오히려 학습에 방해가 될 수 있다.
    • 변수 두 가지$(\gamma, \beta)$를 더 설정한다.
    • $\hat{y}_{i,j}=\gamma_j\hat{x}_{i,j}+\beta_j$
• Batch Normalization은 비선형 연산 전에 적용한다.
• Batch Normalization을 적용하면 학습 시간이 단축된다.
  • 학습이 잘 되는 이유가 이론적으로 설명이 안 된다.

Batch Normalization for ConvNets

Fully-Connected	Convolutional
$x:N\times D$	$X:N\times C\times H\times W$
$\mu, \sigma: 1\times D$	$\mu, \sigma: 1\times C\times1\times1$
$\gamma, \beta: 1\times D$	$\gamma, \beta: 1\times C\times1\times1$
$y=\gamma(x-\mu)/\sigma+\beta$	$y=\gamma(x-\mu)/\sigma+\beta$

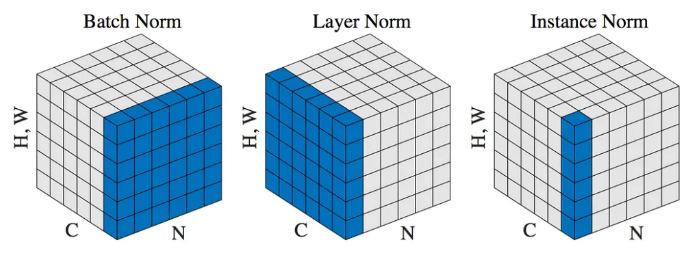
Layer Normalization

• Language Model과 같이 Data sample들 간의 연관이 없을 때 layer normalization이 적용된다.

Batch Normalization	Layer Normalization
$x:N\times D$	$x:N\times D$
$\mu, \sigma: 1\times D$	$\mu, \sigma: N\times1$
$\gamma, \beta: 1\times D$	$\gamma, \beta: 1\times D$
$y=\gamma(x-\mu)/\sigma+\beta$	$y=\gamma(x-\mu)/\sigma+\beta$

Instance Normalization

Fully-Connected	Convolutional
$X:N\times C\times H\times W$	$X:N\times C\times H\times W$
$\mu, \sigma: 1\times C\times1\times1$	$\mu, \sigma: N\times C\times1\times1$
$\gamma, \beta: 1\times C\times1\times1$	$\gamma, \beta: 1\times C\times1\times1$
$y=\gamma(x-\mu)/\sigma+\beta$	$y=\gamma(x-\mu)/\sigma+\beta$