Neural Network
Problem: Linear Classifiers의 한계
- 데이터를 선형으로 분류할 수 없는 경우도 있다.
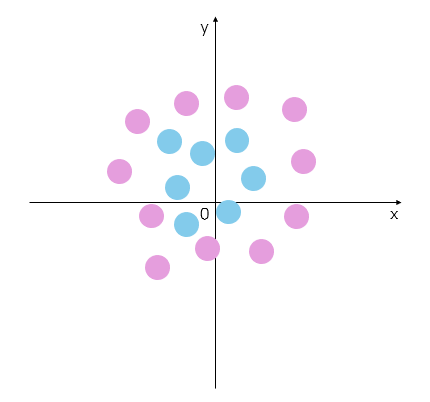
- Solution: Feature 변환
- r=(x2+y2),θ=tan−1(xy)
- 데이터는 변환 전후로 고유한 matching이 가능해야 한다.
- 데이터 분석이 가능해야 한다. 고차원의 경우 데이터 분석이 불가능한 경우가 더 많다.
- 악성코드나 데이터 이동 등, 데이터가 변하지 않아야 한다.
- 하나의 이미지 템플릿으로 class를 구분할 수 없는 경우가 있다.
Neural Network의 등장
- Before: Linear Classification
f=Wxx∈RD,W∈RC×D
- f=W3W2W1x와 같이 선형 연산을 반복하여도 결과는 동일하다.
- 선형 연산을 반복하면 XOR 같은 복잡한 문제를 해결할 수 없다.
- Now: N-layer Nerual Network
f=W2max(0,W1x)W2∈RC×H,W1∈RH×D,x∈RD
- 벡터 내적(선형 연산)을 반복하는 문제를 해결한다.
- 연산의 순서가 결과에 큰 영향을 미친다.
- W2W1=W1W2
- Activation Functions
- 선형 Layer을 중첩할 때 비선형성을 추가하여 표현력을 높이는 역할
- ReLU: max(0,z)
- NN에서 활성화함수가 없으면 layer를 아무리 중첩하여도 선형 분류기에 그치게 된다.
- Sigmoid: σ(x)=1+e−x1
- Tangent: tanh(x)=ex+e−xex−e−x
- ReLU: max(0,x)
- Leaky ReLU: max(0.1x,x)
- Maxout: max(w1Tx+b1,w2Tx+b2)
- Exponential Linear Unit: f(x)={xα(ex−1)x≥0x<0
- Hidden Layer를 거치면 output 벡터에서 하나의 값을 결정하는 데 모든 원소가 관여하게 된다.
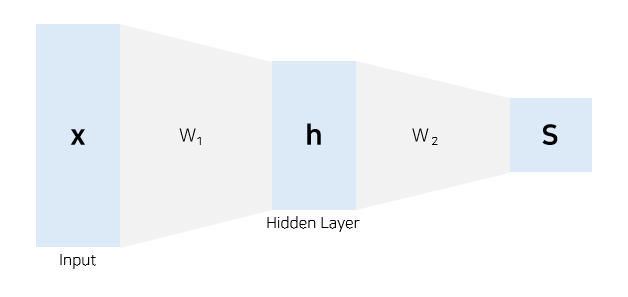
- h=max(0,W1x)=⎣⎢⎡h1h2h3⎦⎥⎤,W2=⎣⎢⎡A1A2A3B1B2B3C1C2C3⎦⎥⎤
- S=⎣⎢⎡A1h1+B1h2+C1h3A2h1+B2h2+C2h3A3h1+B3h2+C3h3⎦⎥⎤
- h의 원소를 결정하는 데 x의 모든 원소가 영향을 미치고, h의 원소는 s를 결정하는 데 영향을 미친다.
- 모든 데이터를 하나의 template으로 처리하는 template matching의 단점을 극복한다.
- 하나의 class score를 결정할 때 다른 class가 서로 섞여 영향을 주어 표현력이 높아진다.
- 다양한 템플릿을 사용하여 클래스의 여러 형태를 다룰 수 있다.
- 결과적으로 해석이 어려운 filter가 도출된다.


