Deep Learning Basics

‍이세현·2024년 3월 18일

Deep Generative Models

Variational Autoencoders (VAEs)
Generative Adversarial Networks (GANs)

VAEs	GANs
단순 암기	구조화되지 않은 상태에서 지식을 표현한다
쉽고 성능이 좋다	학습이 잘 안 된다
안정적이다	창조적인 것과 닮았다
입력 data와 비교하여 평가할 수 있다	맞고 틀림으로만 구분한다

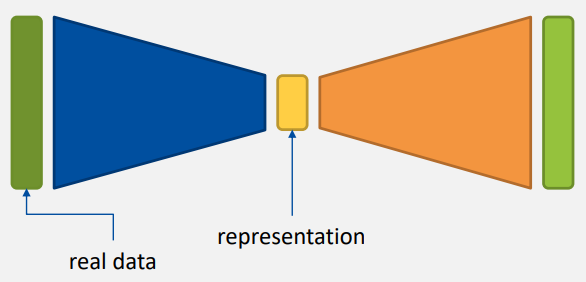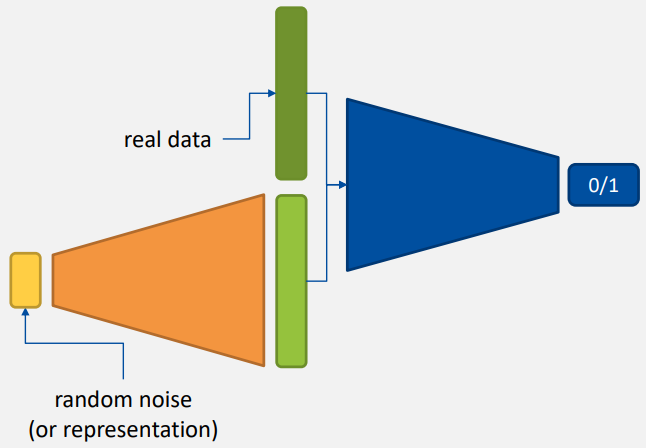주황색 영역 - 생성 단계

GANs에서 지식에 대한 표현이 없는 상태에서 학습하는 것은 매우 오래 걸리므로 VAE의 생성 단계를 사용한다.

The Basics of Machine Learning

Learning Algorithm

어떻게 학습할 것인가

Machine learning algorithm
- 데이터를 통해 학습하는 알고리즘
- 기계가 학습을 하도록 하는 데이터 기반 알고리즘
Definition by Mitchell

어떤 컴퓨터 프로그램이 경험 E에 대해 어떤 종류의 작업 T와 성능 측정 P에 관해서 배운다고 말할 때, 그것은 경험 E에 따라 작업 T에서의 성능이 성능 측정 P에 의해 개선된다면 학습하였다고 할 수 있다.

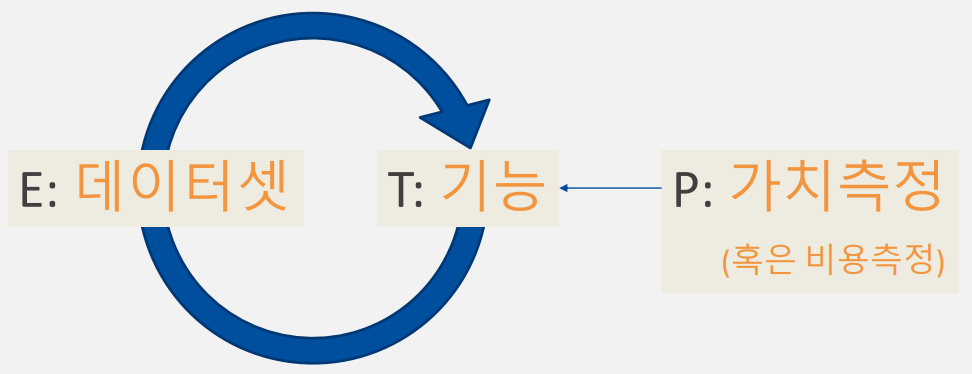
The Task, T

기계가 '어떤 일'을 잘 했으면 좋겠는가 - classification or regression (그림 그리기, 그림 분류하기 등)

ML Task는 보통 ML system이 example을 처리하는 방법으로 설명된다.
ML Task 예시
- Classification
  - C++/JAVA의 분류 문제 표현
```
int classification(Image i) {
	return enum {airplane, ship, ...};
}
```
  - Pytorch로 작성하도록 정의하면 ML
- Classification with missing inputs
  - 누락된 입력이 있는 경우 하나의 classifier가 아닌 여러 모델을 사용하여 학습한다.
- Regression
- Transcription: 일상 언어를 텍스트로 변환하는 것
- Machine Translation - regression
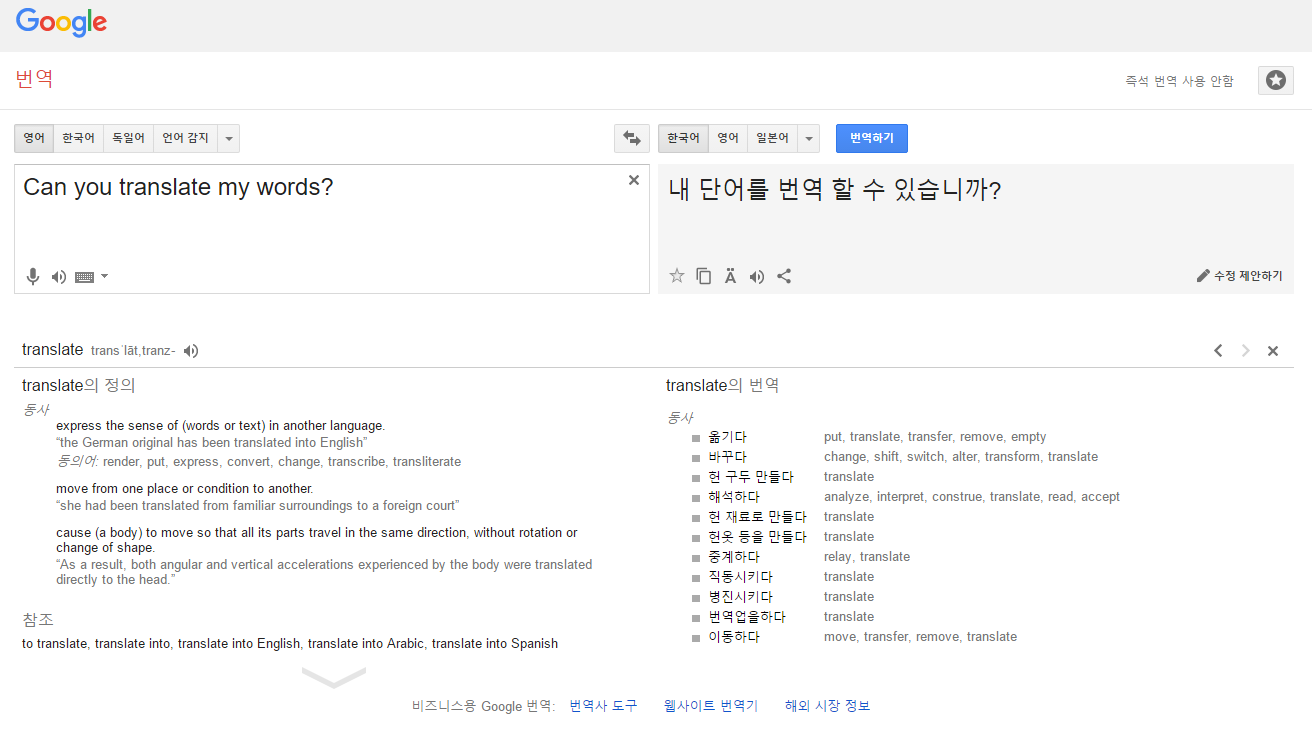
- Structured output: image segmentation 또는 language generating(image to text)과 같이 상호 연관된 변수로 이루어진 구조적인 출력
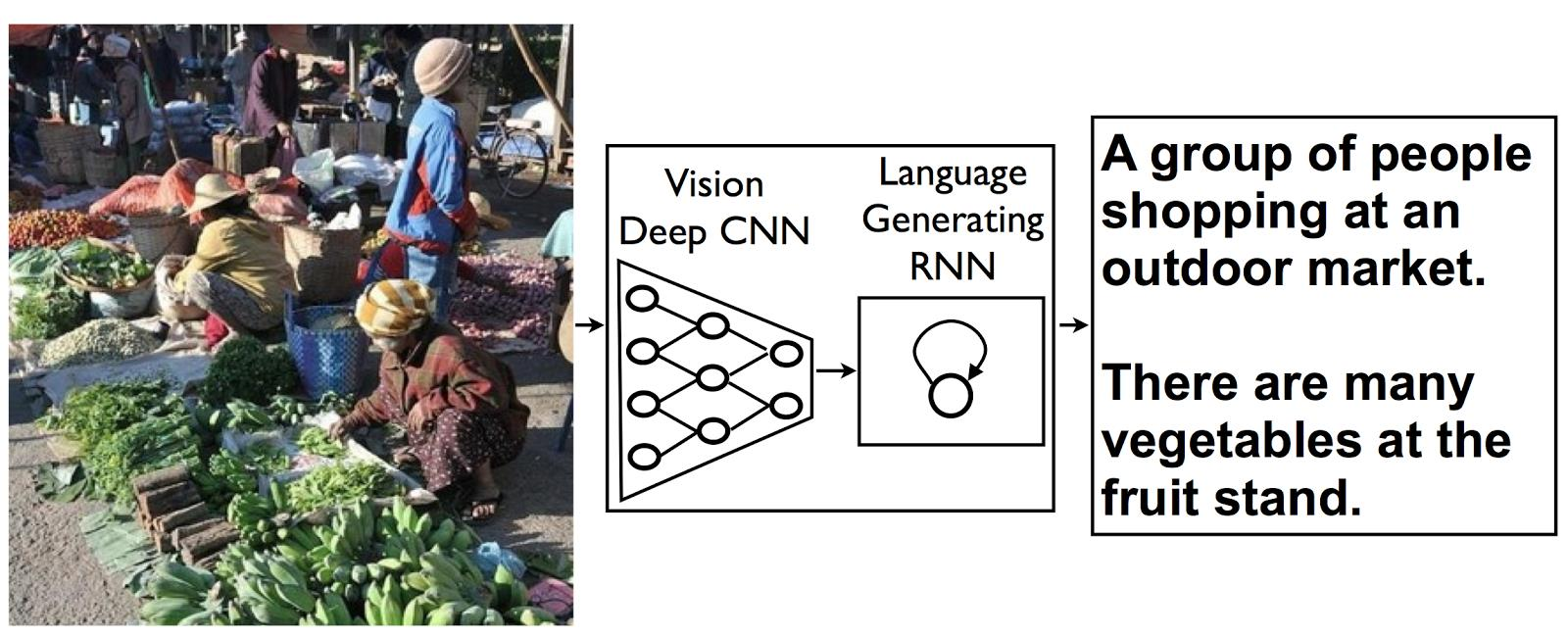
- Anomaly detection: dataset에서 이상한 값을 감지하는 기술로, 보안, 의료 분야에서 사용한다.
- Synthesis and sampling: 데이터 생성과 샘플링(사람 얼굴 만들기) - regression
- Imputation of missing values - unsupervised learning
- Denosing: 잡음이 있는 데이터에서 선명한 데이터를 복원하는 기술
- Density estimation or probability mass function estimation

The Performance Measure, P

Task를 수행하는 ML 알고리즘의 정량적 측정(숫자 비교를 통한 평가)

Classification Task의 경우
- 모델의 정확도 accuracy
  - 올바른 결과를 출력하는 비율
- 모델의 오류율 error rate
  - 틀린 예측은 동일한 penalty를 부과한다.
  - 옳은 예측이면 loss는 0, 틀린 예측이면 loss는 1이다.
  - one-hot encoding
Density estimations - Regression
- 연속적인 값의 숫자
  - 오차의 크기에 따라 penalty가 부과된다.
Test set
- 일반적으로 performance는 training에 사용되는 data의 일부를 test set으로 이용해서 측정한다.

The Experience, E

Experiences는 test를 잘 수행할 dataset이다.
- dataset: 수많은 examples의 묶음
Supervised learning algorithms
- 각 example는 label or target으로 이루어진다.
- 임의의 x 값으로 y를 만드는 예측 모델은 p(y|x)로 표현된다.
Unsupervised learning algorithms
- Data 구성의 유의미한 특성을 학습해야 한다.
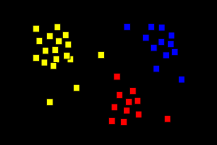
- Label이 없어도 학습할 수 있다.
- 입력이 없어도 measure이 가능하다.
  - 클러스터링의 경우 거리 계산을 통해 measure 가능
- 명시적, 암시적으로 확률분포 p(x)를 학습한다.
Semi-supervised learning
- labeled, unlabeled data가 혼합되어 있는 상태에서 labeled data를 통한 약간의 가이드로 일반화 성능을 끌어올릴 수 있다.

The Basics of Neural Networks

Deep Feedforward Networks

Deep feedforward networks 또는 feedforward neural networks, multi-layer perceptrons
- loop나 branch가 없는 NN의 logic
- Goal: 이상적인 함수 $f^*$ 의 근사치를 구하는 것
Deep Feedforward Networks는 이상적인 함수의 근사치인 $y=f_\theta(x)$ , parameter $\theta$ 를 정의한다.

$f^*(x) \approx f_{\theta}(x)$
- $f^*(x)$ : Ground Truth
- $f_\theta()$ : dataset을 이용한 훈련을 통해 구현해야하는 것
- $\theta$ : Network parameter - training을 통해 업데이트된다.
  
  이때 좋은 방향으로 훈련되고 있는지 P를 통해 확인한다.
Why are they called feedforward?
- 함수를 지나가는 정보의 흐름이 x로부터 시작되어 중간 연산 f를 거쳐 최종적으로 출력 y에 도달한다.
- feedback 연결은 없다.
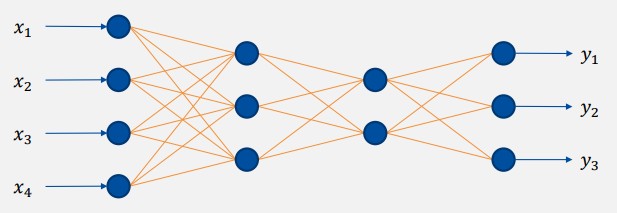
AI의 자료구조는 오직 tensor로 이루어진다.
- 스칼라: 0-tensor
- 벡터: 1-tensor
- 행렬: 2-tensor
- N-tensor
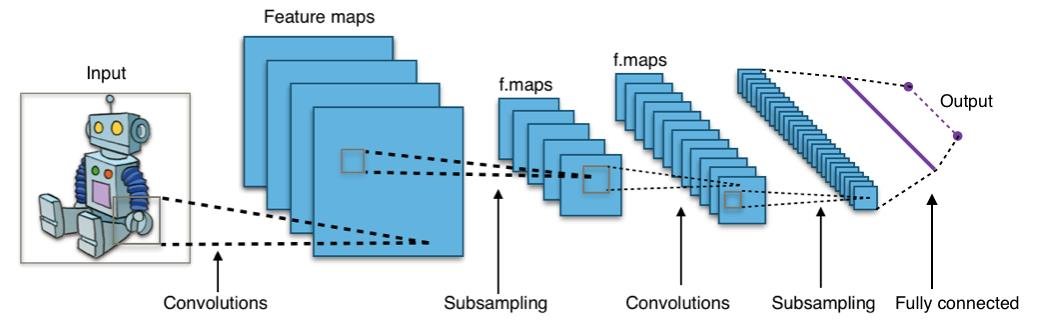
  - 입력이 3-tensor, 출력이 vector인 경우
Some terminologies
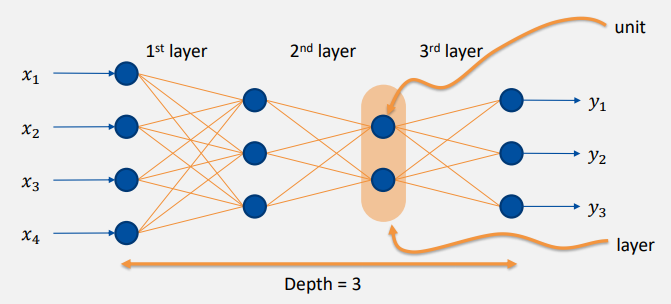
- depth: 모델의 깊이, layer 개수
- unit: layer의 입출력 각각
- layer
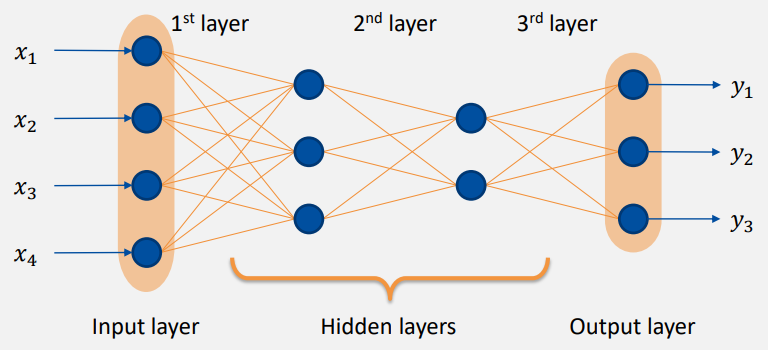
  - input layer
  - hidden layers: black box, 알 필요 없는 layer
  - output layer
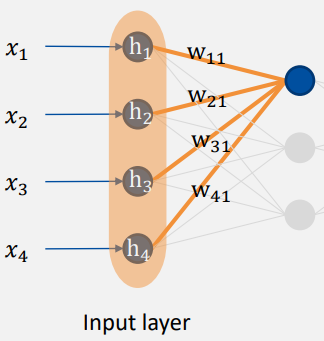
- weights: 입력된 값에 곱하는 가중치
  $x$ : 실제 숫자 - argument
  $h$ : 실제 숫자를 넣기 위한 공간 place holder - parameter
  $w$ : parameter에 곱할 가중치
  
  train을 통해 최적의 w를 구해야 한다.
  
  $y = xA^T$
  와 같이 계산하면 0을 넣었을 때 항상 0이 반환되어 단조로운 문제가 발생하므로 bias로 해결해야 한다.
  $y = xA^T + b$
- Activation functions
  선형함수의 결과값에 비선형을 적용 → 전체 구조는 비선형
  비선형 함수는 여러번 적용해도 되며 매우 깊게 쌓으면 성능이 좋아진다.
A deep network models a non-linear function
- layer를 깊이 쌓을수록, unit이 많을수록 복잡한 기능을 수행한다.
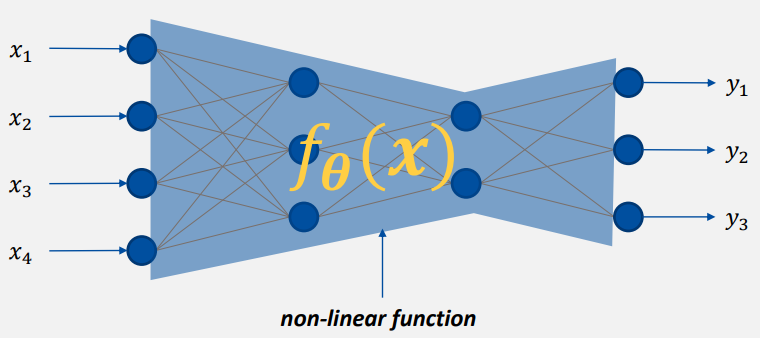
- 모든 선을 표현하기 위한 기호 $\theta$ 는 훈련을 통해 업데이트된다.
- activation function이 포함되어 있으므로 non-linear function이라 한다.
  - Input layer는 function의 input을 다룬다.
  - Training은 최적의 function parameter를 찾는 과정이다.
Deep network는 현재 parameter를 이용해서 output을 예측한다.
이때 완벽한 함수는 아니므로 prediction으로 표현한다.

$y_{pred}$
Loss: 예측값과 실제값의 오차(cost, energy, score)
- ex) $\text{loss} = \| y_\text{pred} - y_\text{true} \| ^ 2$
  $loss(y_{true}, y_{pred}) = loss(\theta)$
- y_true: Ground Truth, dataset
  - 입력 x와 y_true는 사람이 준다.
- y_pred: 훈련 중인 network에서 반환하는 출력
$\theta_{opt} = \arg\min loss(y_{true}, y_{pred}) = \arg\min loss(\theta)$
- 훈련의 목표: loss를 최소화하는 $\theta$ 찾기

Network Training: Minimizing Loss Function

Numerical Computation
- 근의 공식 같은 분석적 접근은 항상 적용할 수 없다.
- 5차 이상의 함수는 근의 공식이 없기 때문에 Gradient Descent가 필요하다.
- numerical approach를 통해 최적의 값을 얻을 수 있다.
- Newton's method
  - 접선와 x축의 교점을 반복적으로 찾으면 근에 도달한다.
  - 시작점이 근의 근처에 있다면 훨씬 빠르게 근에 도달한다.
  - first order, second order approoximation으로 확장할 수 있다.
Gradient-Based Optimization
- 대부분의 deep learning algorithms은 loss를 최소화하는 것과 같은 최적화를 포함한다.
  
  $\theta_{opt} = \arg\min l(\theta)$
- cost function $l(\theta)$ 를 줄이는 방법
  - $l'(\theta) \approx \frac{{l(\theta + \epsilon) - l(\theta)}}{{(\theta + \epsilon) - \theta}} ⇨ l(\theta + \epsilon) \approx l(\theta) + \epsilon l'(\theta)$
  - 기울기 방향으로 이동하면 원래 loss보다 증가하므로 반대 방향으로 가야한다.
- Gradient descent
  - θ를 미분 반대 방향으로 조금씩 이동하면 $loss(\theta)$ 를 줄일 수 있다.
  - $\theta ← \theta - \epsilon sign(l'(\theta))$
  - $\epsilon$ : learning rate
- Critical points: $l'(\theta)$ 가 0이 되는 지점
  - Local minimum, local maximum, saddle point 등
- Global minimum: $l(\theta_{opt})$
- $l(\theta)$ 를 최소화하는 방법
  - 편미분
- $l(\theta)$ 의 기울기, $\nabla l(\theta)$
  $\nabla l(\theta) = \begin{bmatrix} \frac{{\partial}}{{\partial \theta_1}} l(\theta) \\ \begin{array}{c} ⋮ \\ \end{array} \\ \frac{{\partial}}{{\partial \theta_n}} l(\theta) \\ \end{bmatrix}$
  $\theta ← \theta - \epsilon \nabla l(\theta)$
- learning rate ε를 정하는 방법
  - 작은 상수를 선택한다.
  - 점진적으로 숫자를 줄인다.
  - 주어진 방향으로 단계적으로 loss를 최소화하는 값을 찾는다.