Linear Regression with One Variable

Model Representation

Example: Housing Prices Prediction

1. Task 분류

   • Regression Problem: real-value
   • Supervised Learning: Given "right answer"

2. Notation

   • $m$: 훈련 데이터 개수
     • 좋은 데이터가 많으면 학습에 유리하다.
   • $x$'s: 입력 변수 / features - $(\text{feet})²$
   • $y$'s: 출력 변수 / target variable - $\text{price}$

3. 전체 개요
   

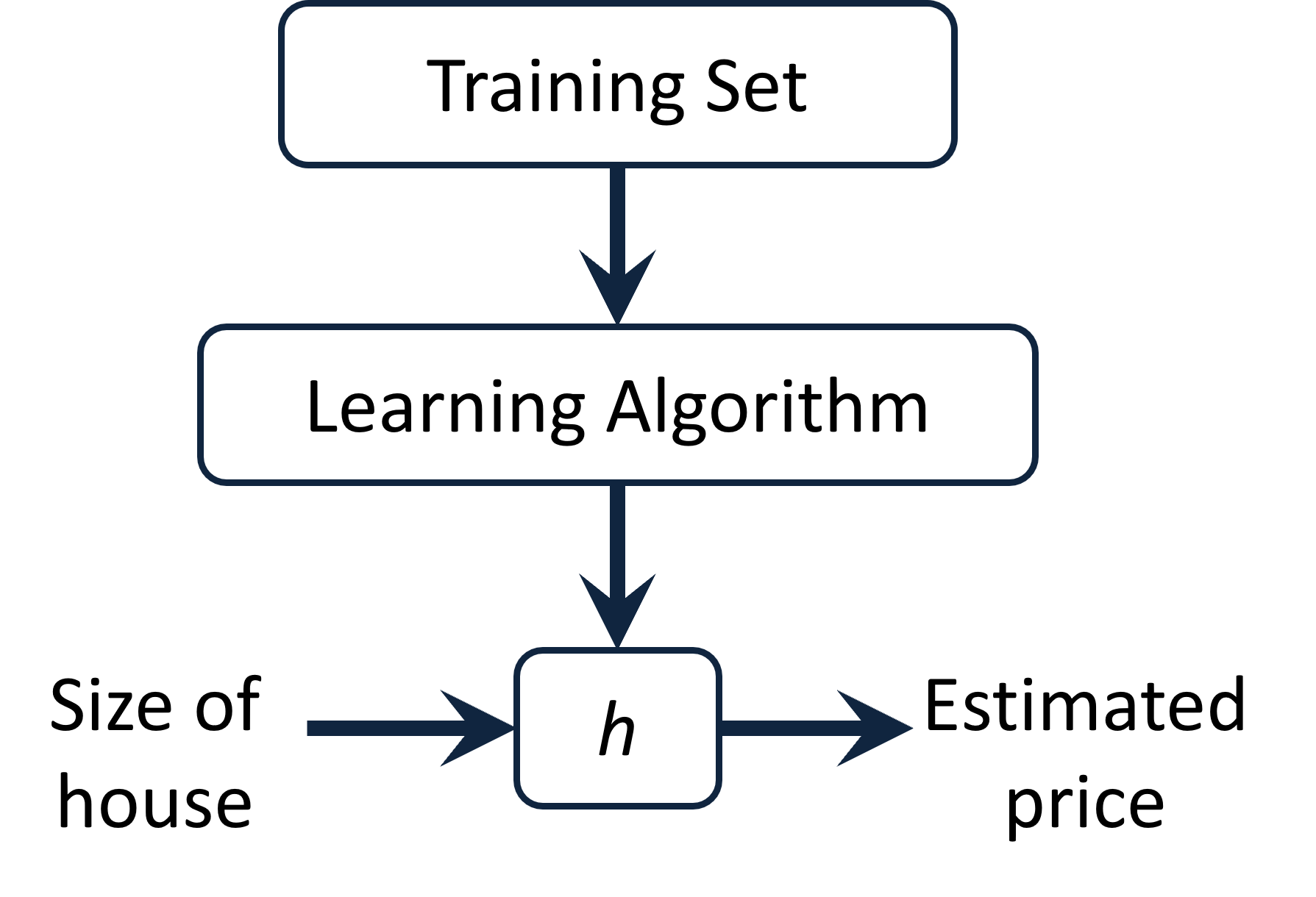
   • Training Set - $E$
   • Learning Algorithm - Supervised Learning or Cost Function
   • Size of house - 입력 $x$
   • $h$ - 데이터 기반 function, $\theta$
   • Estimated price - 예측 가격

   $h$를 표현하는 방법

   • $h(x)$ = $θ₀ + θ₁x$ - 선형적일 것이라고 가정
     • 변수가 한 개인 linear regression
     • Univariate linear regression

Cost Function

1. Training Set - $E$

   Size in $\text{feet}²(x)$	Price in $100's(y)$
   2104	460
   1416	232
   1534	315
   852	178

2. Hypothesis
   $h(x) = θ₀ + θ₁x$

3. $θᵢ$'s: parameters

   $θᵢ$'s를 구하는 과정 → Machine Learning
   $θᵢ$'s를 적절히 구했는지 측정하고 판단해야 한다.
   Idea: 실제 정답 $y$와 $h(x)$가 가장 근사해지는 $θ₀$, $θ₁$를 선택한다.

Cost Function Intuition I

Simplified

1. Hypothesis
   $h(x) = θ₁x$
2. Parameters
   $θ₁$
3. Cost Function
   $J(\theta_1) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2$
4. Goal
   $J(θ₁)$를 최소로 만드는 $θ₁$ 구하기

Cost Function Intuition II

1. Hypothesis
   $h(x) = θ₀ + θ₁x$
2. Parameters
   $θ₀$, $θ₁$
3. Cost Function
   $J(\theta_0, \theta_1) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2$
   $θ₀$, $θ₁$ 두 가지 변수를 모두 고려해야 한다.
   그래프를 그리면 contour 형태로 나타난다.
4. Goal
   $J(θ₀, θ₁)$를 최소로 만드는 $θ₀$, $θ₁$ 구하기
   Global solution에 도달하여도 오차는 0이 되지 않는다.

Gradient Descent

경사하강법: $J(θ₀, θ₁)$를 최소로 만드는 $θ₀$, $θ₁$ 구하기 위한 방법

개요

• Start with some $θ₀$, $θ₁$ - 시작점은 항상 달라질 수 있다.
• $J(θ₀, θ₁)$를 줄이는 방향으로 $θ₀$, $θ₁$를 계속 수정한다.
  • 기울기: 가장 가파르게 올라가는 방향
  • 기울기 반대 방향으로 이동하며 최저점을 찾아야 한다.
• 시작점이 달라지기 때문에 항상 일정한 결과를 도출할 수 없다.

Gradient Descent Algorithm

수렴할 때까지 아래 식을 반복한다.

• 이론적으로는 기울기가 0이 될 때까지 반복해야 하지만 실제로는 불가능하므로 사람이 정도껏 멈추어 주어야 한다.
• $\theta$ 값들은 동시에 update해야 한다.
  
• $-\alpha$: 기울기의 반대 방향으로 learning rate 만큼 값을 갱신한다.
  • learning rate: 얼마큼 update 할 건지 결정하는 실험적 변수
    • P, T, E에 따라 크게 달라진다
  • $α$가 지나치게 작으면 연산량이 많아지고 수렴이 느려진다.
  • $α$가 지나치게 크면 수렴하지 않고 발산한다.

Gradient Descent Intuition

• 모델이 정해지면 loss function은 변하지 않는다.
  • 시작점에 따라 결과가 달라지기 때문에 초기화가 매우 중요하다.
    
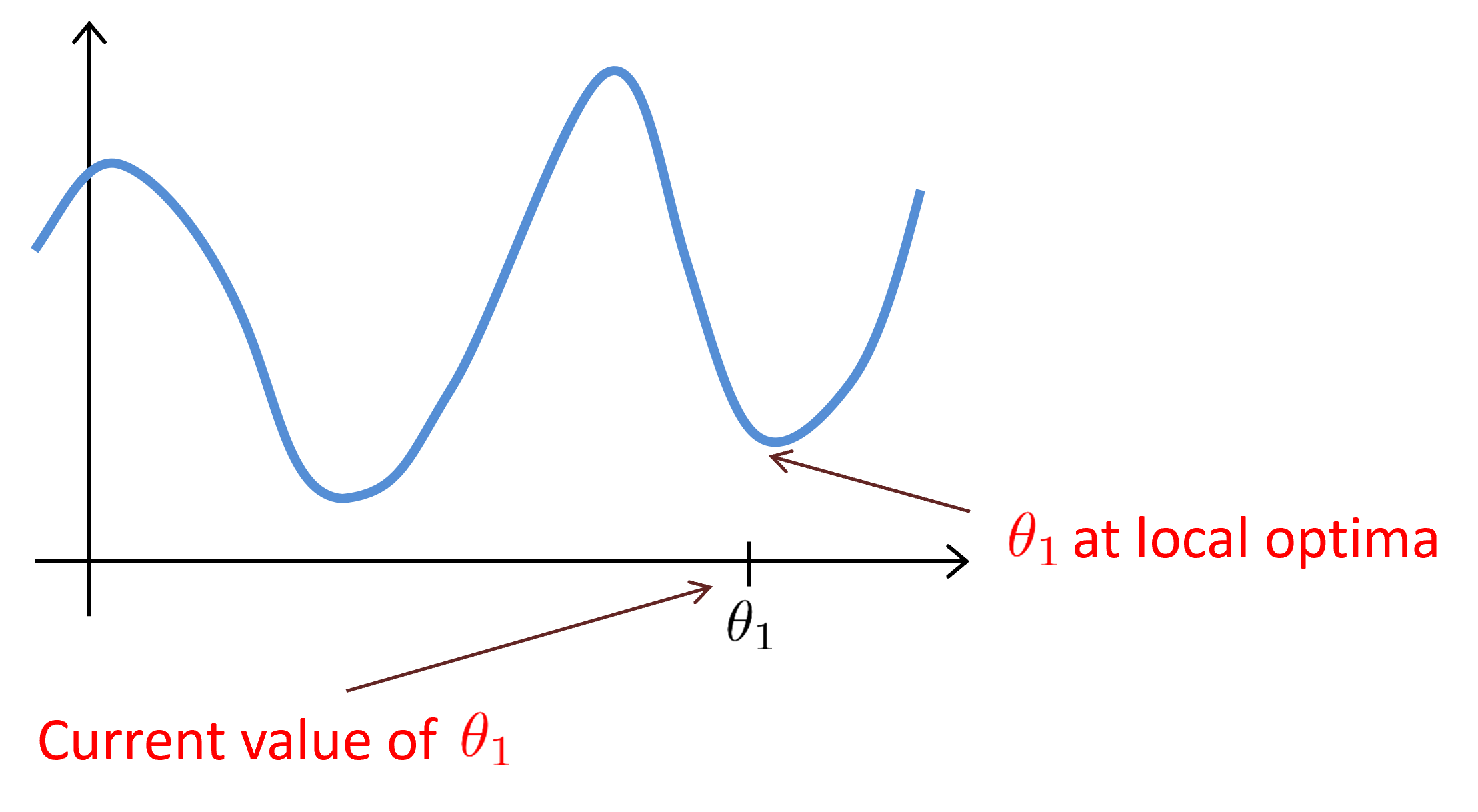
  • local optima는 최적의 solution이 아니다.
• 경사하강법은 learning rate가 고정되어 있어도 local minimum에 수렴할 수 있다.
• Local minimum에 도달하면 경사하강법은 자동적으로 더 작은 단계를 취한다. 따라서 learning rate를 줄일 필요가 없다.

Gradient Descent for Linear Regression

Gradient Descent Algorithm

수렴할 때까지 반복한다.

• $θ₀$ 업데이트 == $θ₀$ 편미분
  $\theta_0 := \theta_0 - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_\theta (x^{(i)}) - y^{(i)})$
• $θ₁$업데이트 → $θ₀$의 기울기는 알 필요 없으며 $θ₁$의 기울기를 알아야 한다.
  $\theta_1 := \theta_1 - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_\theta (x^{(i)}) - y^{(i)}) \cdot x^{(i)}$
• $θ₀$, $θ₁$은 동시에 업데이트 한다.

Linear Regression Model

데이터가 $m$개일 때 손실 함수 $J(θ_0, θ_1)$

Convex function

Bowl-shaped의 convex function의 경우 gradient descent를 통해 항상 최적을 결과를 도출할 수 있다.

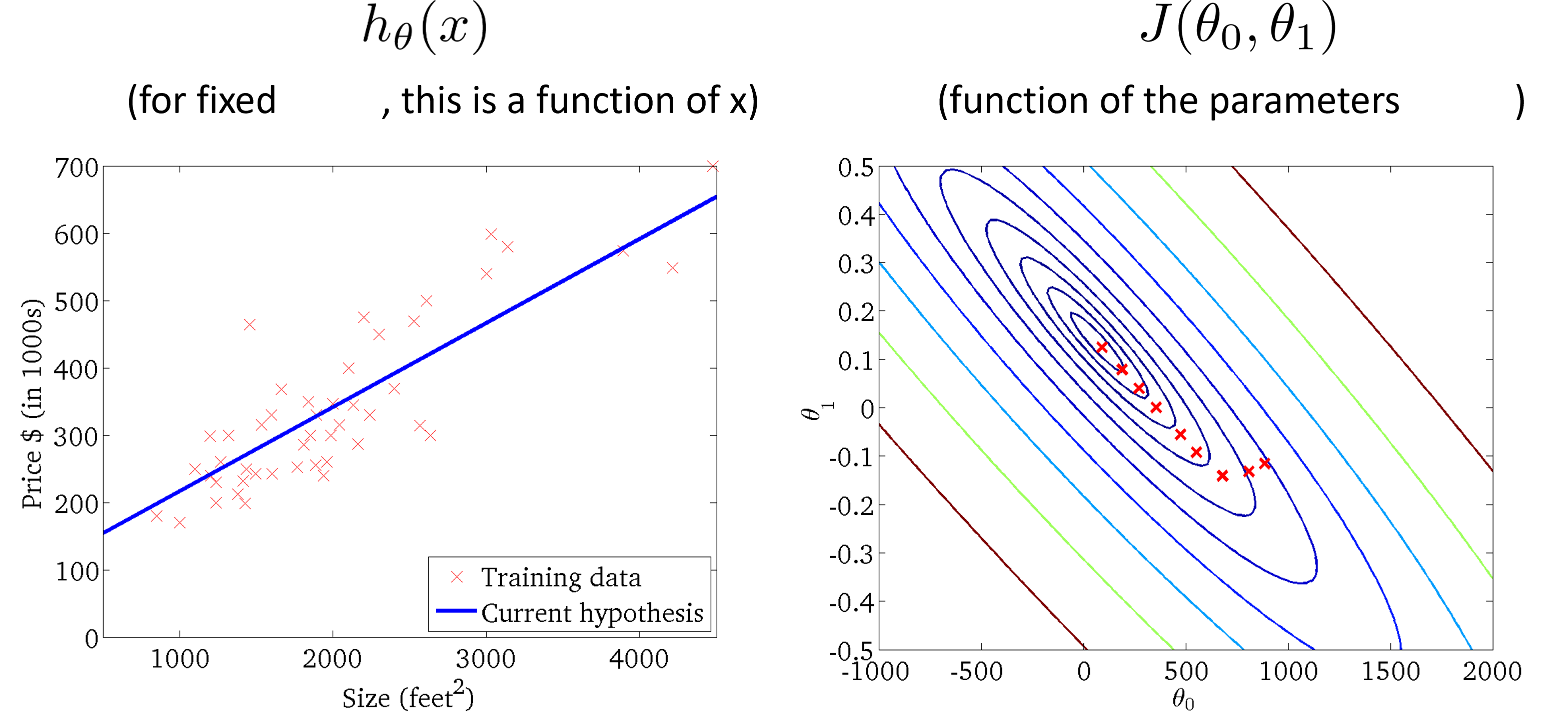
도달한 결과가 위와 같고 error가 잔재할 때 차원을 변경하는 등 가설을 변경하여 데이터를 더 잘 표현하는 함수를 찾아야 한다.

"Batch" Gradient Descent
Training sample을 모두 사용해서 gradient descent를 수행하는 것
cf) Mini-batch, Stochastic Gradient Descent