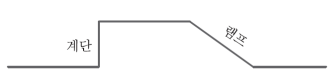
Edge란 Color 값 또는 명암 값의 차이가 명확한 사물의 경계 부분을 뜻한다. 에지는 매칭에 용이한 선분이나 곡선으로 변환할 수 있다. 하지만 너무 밝거나 어두운 때 실종된 에지 (거짓 부정), 거짓 에지 (거짓 긍정) 에지가 발생하는 문제가 있다. 이러한 오류를 어떻게 최소화할 수 있을까.
에지 검출의 기초
- 원리
- 물체 내부나 배경은 변화가 없거나 작은 반면, 물체의 경계는 변화가 크다. 이 원리에 따라 에지 검출 알고리즘은 명암, 컬러 또는 텍스처의 변화량을 측정하고, 변화량이 큰 곳을 에지로 검출한다.
- Surface Normal Discontinuity: 에지만으로 어떤 물체인지 구분 가능하다.
- Depth Discontinuity: 배경과 물체를 구분할 수 있다.
- Surface Color Discontinuity: 색 정보로 에지를 검출할 수 있다.
- Illumination Discontinuity: 조명, 그림자 정보를 검출할 수 있다.
- 물체 내부나 배경은 변화가 없거나 작은 반면, 물체의 경계는 변화가 크다. 이 원리에 따라 에지 검출 알고리즘은 명암, 컬러 또는 텍스처의 변화량을 측정하고, 변화량이 큰 곳을 에지로 검출한다.
- 에지 정보만으로도 물체의 정보, 빛의 방향 등의 정보를 얻을 수 있다.
- 조명 환명이 변화하면 검출되는 속성 또한 모두 바뀐다.
디지털 영상의 미분
- 1차원
-
연속 공간에서 미분
-
디지털 (이산) 공간에서 미분
- 의 최솟값이 로 오른쪽 픽셀 값 과의 차이를 의미한다.
- 이 연산은 [-1, 1] 마스크로 수행할 수 있다.
순서 0 1 2 3 4 5 6 7 8 9 디지털 영상 2 2 3 2 3 5 9 9 8 9 의 도함수 0 1 -1 1 2 4 0 -1 1 -
-
- 계단 에지와 램프 에지
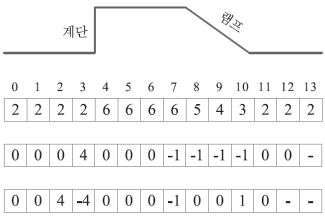
- 자연 영상에서는 주로 명암값이 서서히 변하는 램프 에지가 나타난다.
- 계단 영역의 경우 입력된 디지털 영상의 1차 도함수에서 0이 아닌 영역이 한칸으로 나타난다.
- 램프 영역의 경우 0이 아닌 영역이 네 칸으로 edge가 굵게 드러난다.
- 이 문제를 해결하게 위해 2차 도함수를 구해 edge의 시작과 끝(4와 -4, -1과 1)을 표현한다.
- 2차 도함수는 [1, -2, 1] 형태의 마스크로 계산할 수 있다.
- 차선의 경우 계단 에지 네개가 검출된다.
- 램프 에지에서의 미분
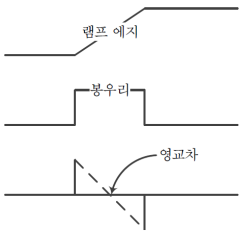
- 램프에지는 두꺼운 에지이다. 따라서 1차 미분에서 봉우리를 검출하거나 2차 미분에서 edge의 시작과 끝의 가운데 위치인 영교차를 찾아 에지를 검출한다.
- 에지의 특성
- 에지에는 이미지 강조가 급격하게 변하는 구간이다.
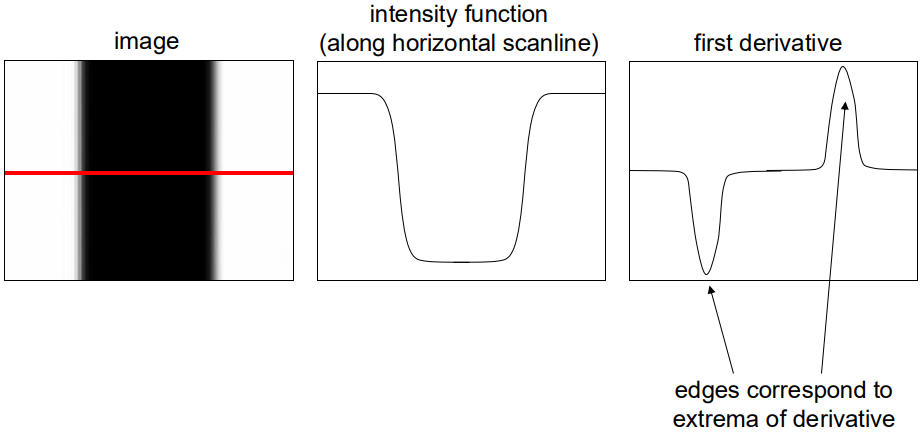
- 하지만 실제 영상에는 noise가 섞여있기 때문에 픽셀 간 차이가 부각되어 거짓 에지가 검출될 수 있다.
- 일반적으로 노이즈가 클수록 Difference Filter는 더 강하게 반응한다.
- 필터를 씌워 문제를 해결할 수 있다.
- 계단 에지를 검출하기 위해 2중 for loop을 반복하며 convolution 연산을 적용해 램프 에지 형태로 검출하고 이를 미분하여 (-1, 1 마스크) peak point를 찾는다.
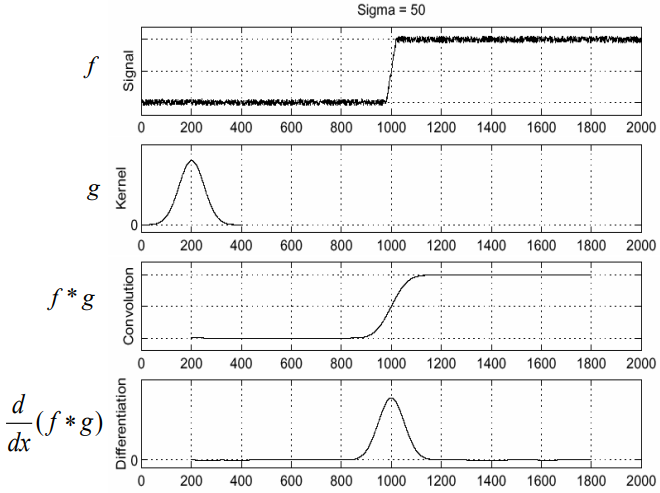
- 미분은 Convolution과 같고 convolution은 합성 함수이므로
- 1에서 2회의 convolution을 하나의 마스크로 결합하여 연산 횟수를 줄일 수 있다.
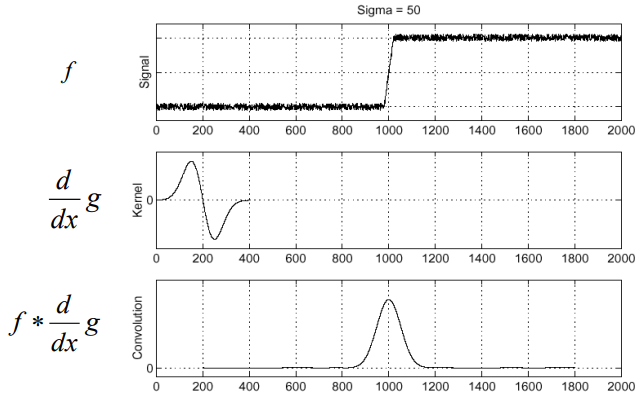
- 계단 에지를 검출하기 위해 2중 for loop을 반복하며 convolution 연산을 적용해 램프 에지 형태로 검출하고 이를 미분하여 (-1, 1 마스크) peak point를 찾는다.
- 에지에는 이미지 강조가 급격하게 변하는 구간이다.
- Gaussian Filter의 변형
- x-direction filter는 x축 변화에 나타내므로 세로축을 검출하기에 용이하다.
- y-direction filter는 가로축을 검출하기에 용이하다.
에지 모델과 연산자
- 현실에서는 잡음 때문에 스무딩이 필요하다. 이를 위해 인 연산으로 확장하면 [-1, 0, 1] 마스크를 적용해야 한다.
- 2차원으로 확장하면 상하좌우를 모두 고려하기 위해 [-1, 0, 1], [-1, 0, 1] 마스크를 적용해야 한다.
- 정방형으로 확장하여 스무딩 효과를 적용할 수 있다.
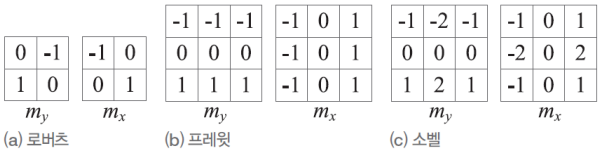
- 로버츠 연산자로 대각선 에지를 검출할 수 있다.
- 프레윗 연산자로 y축, x축 미분을 할 수 있다.
- 소벨 필터는 smoothing과 에지 검출이 동시에 적용되어 에지 검출이 더 잘 된다.
에지 강도와 에지 방향
- 에지 검출 연산
-
Gradient: 컬러나 명암 값이 바뀌는 방향과 크기를 나타내는 벡터
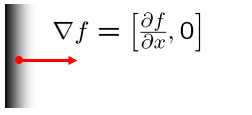
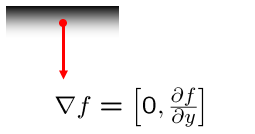
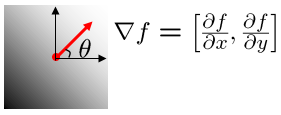
상하 명암차이와 무관하게 세로 에지가 검출된다. 세로 방향으로 서서히 변화한다. 명암값 변화를 나타내는 벡터
-
- 에지 강도 (의 magnitude):
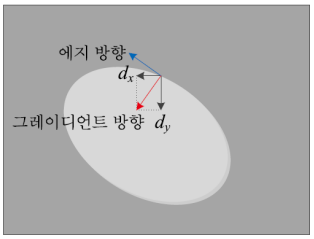
- Gradient 방향:
- Gradient 방향은 에지 방향과 직교한다.
선분 검출
에지 연결과 선분 근사
- 에지 연결과 표현
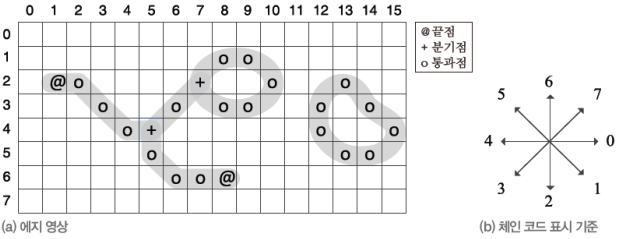
- 입력 이미지는 이고 에지 정보는 입력의 20% 정도에 불과한다.
- 에지 토막의 에지 열과 체인 코드로 표현하면 간략하게 표현 가능하다.

- 선분 근사
- 두 끝점을 잇는 직선으로부터 가장 먼 점까지의 거리 가 임계값 이내가 될 때까지 선분 분할을 재귀적으로 반복하는 것
- 픽셀이 이산적이기 때문에 선분 근사는 거의 사용되지 않는다.
허프 변환
- 허프 변환
- 에지 연결 과정 없이 선분 검출
- 에지 영상 정보를 직선의 방정식으로 반환하는 것
- 영상 공간 를 기울기 절편 공간 로 매핑
- 공간을 변환한다는 의미에서 Hough Transform이라고 한다.
- 수직선의 기울기가 인 문제
- 극좌표계를 사용하여 해결한다.
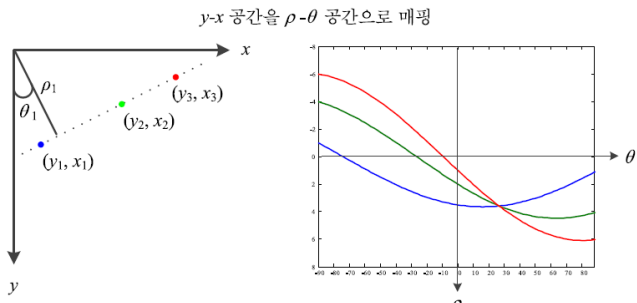
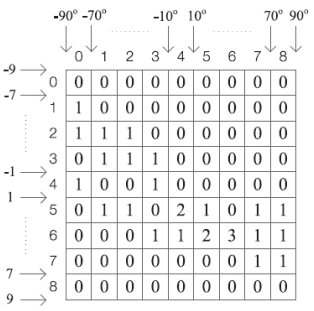
- 양자화된 누적 배열을 이용하여 밀집된 곳의 값을 도출한다.
- 하나의 점을 지나는 직선()의 개수는 무수히 많지만 두 개의 점을 지나는 직선()은 하나뿐이다. 따라서 모든 점(에지)에 대해 그 점을 지나는 직선()에 대한 정보가 가장 많이 겹치는 직선이 Hough Transform의 출력이 된다.
- 극좌표계를 사용하여 해결한다.
Voting Schemes
- 모든 파라미터를 이산 공간에서 표현한다.
- 각 특징점이 이산 공간 어느 위치에 존재하는지 표시한다.
- 가장 많이 표시된 곳을 선택한다.
Algorithm Outling
- 누적 배열 를 초기화한다.
- Edge point에 대해 계산한다.
- For
- 가 최대인 local maximum을 찾는다.
- Circle의 경우 직선이 없으므로 극좌표계에서 표현된 선분들이 한 점에서 만나지 않는다.
- 원 검출을 위해서는 3차원 누적 배열을 사용한다.
- 반지름을 늘려가며 voting
- 각 도형에 따라 정해진 vectors가 있고 이는 패턴 인식에 활용된다.
- Hough Transform은 noise에 취약한 문제가 있다.
RANSAC
- Effect of noise
- Noise로 인해 극좌표계에서 표현된 선분들이 한 점에서 모이지 않는 문제가 발생한다.
- Inlier를 찾아 어떤 모델을 적합시키는 기법으로, 잡음이 있어도 직선을 검출할 수 있다.
- 난수를 생성하여 인라이어 군집을 찾기 때문에 임의성을 지닌다.
- Least Squared error
- 오차가 최소인 직선을 구하는 방법으로 Outlier에 취약하다.
- 결과로 도출되는 직선이 항상 하나로 동일하지만 시간 소요가 크다.
- 원리
- 입력 샘플 집합에서 임의로 두 점을 선택하여 직선을 긋고 설정한 margin 내에 포함된 샘플 수가 임계 이상이 될 때까지 반복한다.
- RANSAC은 noise의 영향을 최소화하기 때문에 최적화에서도 활용된다.
