Lateral Control

‍이세현·2025년 5월 25일

Lane Keeping Assistance System

LKAS는 차량이 차선을 벗어나지 않도록 자동으로 조향을 조절하는 시스템이다. 운전자가 직접 조향을 하지 않아도 자동차가 도로 위의 차선을 따라 안정적으로 주행할 수 있도록 도와준다. 카메라와 센서로 현재 차량이 차선에서 얼마나 벗어났는지( $e_1$ ), 차량의 방향이 도로와 얼마나 틀어졌는지( $e_2$ ) 측정하여 차량을 원래 차선으로 되돌리도록 조향을 보정한다.

LKAS 제어 구조

카메라, GPU, IMU를 이용해서 도로 중심선과 차량 상태를 감지하면 제어기는 오차 $e_1, e_2$ 를 기반으로 제어량을 계산하여 실제로 핸들을 돌리는 구조로 동작한다.

Dynamic Bicycle Model 기반 상태공간

상태 변수 $e_1, e_2$ 는 LKAS의 핵심이다.

$e_1$ : 차량 중심이 차선 중심에서 얼마나 벗어났는지 나타내는 횡방향 오차로, $e_1>0$ 이면 차량이 차선의 오른쪽으로 벗어난 것이다.
$e_2$ : 차량이 도로 중심선에 비해 얼마나 기울어져 있는지 나타내는 헤딩각도 오차로, $e_2>0$ 이면 차량이 도로보다 왼쪽을 향하는 것이다.

이 오차를 줄이는 방향으로 핸들을 자동 조절하는 것이 제어기의 목표이다.

차량이 바퀴 두 개 달린 Bicycle Model이라고 가정한다면, 이 모델은 속도, 조향각, 타이어 힘 들을 바탕으로 회전을 설명할 수 있다. 예를 들어 차량이 일정 속도 $V_x$ 로 선회반경 $R$ 을 유지하면서 움직이고 있을 때 먼저 두 가지 개념을 잡아야 한다.

$\dot\psi_\text{des}=\frac{V_x}{R}$ : 목표 요레이트
$a_{y,\text{des}}=\frac{V_x^2}{R}=V_x\dot\psi_\text{des}$ : 목표 횡가속도

차량이 차선에서 얼마나 벗어났는지 측정하려면 두 개의 오차항의 수식을 정의해야 한다.

$\ddot{e_1} =a_y-a_{y,\text{des}} = \ddot{y}+V_x\dot\psi-V_x\dot\psi_\text{des}$ : 횡가속도 오차
$e_2=\psi-\psi_\text{des}$

차량 속도 $V_x$ 가 일정하다고 가정하였으므로 $\ddot{e}_1$ 은 적분했을 때 다음과 같다.

\dot{e}_1=\dot{y}+V_x(\psi-\psi_\text{des})

이 두 값( $e_1,e_2$ )이 0이면 차량이 완벽하게 중심선을 따라가고 있는 것이고, 값이 클수록 많이 벗어난 것이다.

이 오차들을 포함한 시스템 전체( $x$ )를 상태공간으로 표현하면 다음과 같은 상태방정식을 얻게 된다.

\frac{d}{dt} \begin{bmatrix}e_1 \\ \dot{e}_1 \\ e_2 \\ \dot{e}_2 \end{bmatrix} = Ax+B_1\delta+B_2\dot\psi_\text{des}

차량이 중심선에서 벗어나지 않도록 핸들을 자동으로 조정할 때 사용하는 것이 상태 피드백 제어기이다. 제어 입력, 즉 조향각은 다음과 같이 설계된다.

\delta=-Kx=-k_1e_2-l_2\dot{e}_1-k_3e_2-k_4\dot{e}_2

$x$ 는 현재 시스템의 상태이고, $K$ 는 설계해야 하는 gain 값이다. 즉, 오차가 클수록 핸들을 더 크게 꺾어서 위치를 보정하게 된다.

이 제어기를 제대로 동작하게 하려면, 제어 시스템의 고유값을 조절해줘야 한다. 이를 위해 Pole Placement 기법을 사용한다.

차량 경로 제어 알고리즘

Pure Pursuit

Pure Pursuit은 차량이 특정 경로를 따라가기 위해 사용하는 대표적인 경로 추종 알고리즘 중 하나이다. 차량은 일정 거리 앞에 있는 목표 지점을 추적하도록 조향각을 계산한다. 핵심 아이디어는 차량 뒤 축 중심을 기준으로, 경로 상 일정 거리 떨어진 점을 목표로 회전 반경 $R$ 을 결정하고, 해당 반경에 맞는 조향각 $\delta$ 를 계산하는 것이다.

Pure Pursuit은 Kinematic Bicycle Model에 기반한다. 기하학적으로 조향각 $\delta$ 를 유도할 때 차량이 회전 반경 $R$ 로 곡선을 그리며 선회한다는 가정이 필요하다. 차량의 회전 중심을 기준으로 삼각형을 형성하면 아래와 같은 삼각 함수를 통해 조향각을 유도할 수 있다.

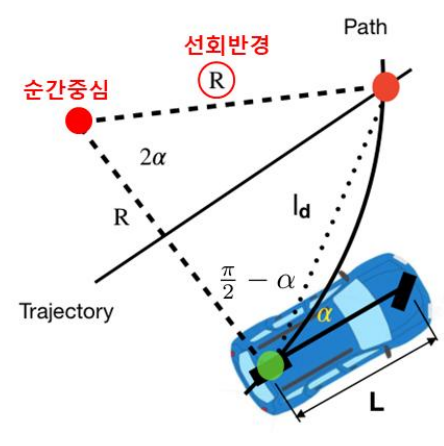
\frac{l_d}{\sin2\alpha}=\frac{R}{\sin(\frac{\pi}{2}-\alpha)}\quad\rightarrow\quad \frac{l_d}{2\sin\alpha\cos\alpha}=2R\quad\rightarrow\quad\kappa=\frac{1}{R}=\frac{2\sin\alpha}{l_d}

여기서 $\alpha$ 는 차량 후륜과 목표 지점 사이의 헤딩각이고, $l_d$ 는 전방주시거리, $L$ 은 휠베이스일 때 조향각은 다음과 같이 유도된다.

\delta_f=\tan^{-1}\frac{L}{R}=\tan^{-1}\kappa L=\tan^{-1}\Big(\frac{2L\sin\alpha}{l_d}\Big)

보통 도로 위 실제 차량은 도로 중심선에서 얼마나 벗어났는지 측정할 수 있다. 이 오차를 통해 조향각을 단순하게 다음과 같이 유도할 수 있다.

\delta_f\approx\frac{2L}{l_d^2}e

이 조향각은 경로 오차 $e$ 에 비례하고, 전방주시거리 $l_d$ 의 제곱에 반비례하다. 이 관계는 차량이 경로에 빨리 복귀하려면 어떻게 조향해야 하는지 직관적으로 보여준다.

전방주시거리 $l_d$ 는 제어 성능을 좌우하는 중요한 파라미터이다.

$l_d$ 가 크면 경로 오차가 커도 조향각은 작게 계산되어 부드럽게 움직이지만 반응이 느릴 수 있다.
$l_d$ 가 작으면 경로 오차가 작아도 조향각이 크게 계산되어 빠르게 반응하지만 과잉 반응할 수 있다. (초보운전)

속도에 따라 전방주시거리를 조절할 수도 있다.

고속 주행 시 $l_d$ 가 증가하므로 경로 오차가 크더라도 조향각이 작아서 안정적으로 조향할 수 있다.
저속에서는 $l_d$ 가 작아서 민감하게 반응한다.

Pure Pursuit는 기하학적인 방법이므로 구현이 쉽고 직관적이지만, 타이어 슬립이 발생하는 고속 상황, 또는 정확한 경로 오차 계산이 어려운 경우에는 정확도가 떨어질 수 있다. 따라서 실내 자율주행 차량, 저속 주행에 주로 사용된다.

Stanley Control

Stanley Control은 차량이 도로 위 목표 경로를 잘 따라가게 만드는 방식이지만 Pure Pursuit과 달리, 전방주시거리 $l_d$ 를 사용하지 않고도 정확하게 조향각을 계산할 수 있다. 핵심 아이디어는 차량의 앞바퀴 중심을 기준으로 잡고 경로 오차와 헤딩 오차를 사용하는 것이다.

횡 경로오차 $e$ : 차량 앞바퀴 중심에서 목표 경로까지의 수직 거리
헤딩 오차 $\psi$ : 차량이 향하고 있는 방향과 경로가 향하는 방향의 각도 차이

조향각 $\delta_f$ 는 다음 두 항의 합으로 계산된다.

헤딩오차고려: 목표 경로의 방향과 차량 축방향을 일치시키기 위한 조향각도 (Feedforward 항)
$\delta_f=\psi$
- 차량이 목표 경로 방향을 향하도록 조향각을 조절한다.
경로오차고려: 아래 조건을 고려한 control law 설정 (Feedforward 항): Pure-pursuit과 유사
- 경로 오차에 비례
- 차량 속도를 고려 (예: 고속에서 작은 조향각도) $\delta_f=\tan^{-1}\Big( \frac{ke}{v_f} \Big)$
- $k$ 는 튜닝 파라미터로, 경로 오차에 대한 민감도이다.
- 경로에서 벗어난 거리만큼 조향각을 조절한다. 차량 속도가 느릴수록 조향각을 더 크게 조절하여 빠르게 경로에 복귀한다.

두 항을 합치면 최종 조향각은 다음과 같이 계산된다.

\delta_f=\psi+\tan^{-1}\Big( \frac{k\dot e}{v_f} \Big)

Control Law를 구성하는 두 항의 크기에 따라 경로를 제어한 결과

Stanley 알고리즘은 차량이 경로를 따라가도록 지속적으로 방향을 조절한다.

속도가 빠르면 조향각이 작아지므로 경로 오차를 부드럽게 수정한다.
속도가 느리면 조향각이 커지므로 경로 복귀를 빠르게 유도한다.
목표 경로에 가까워질수록 경로 오차는 감소하고, 조향각도 점차 줄어든다.

속도 $v_f$ 가 너무 작아지면 조향각이 과도하게 커질 수 있기 때문에, 분모어 보정항 $k_s$ 를 추가하여 조정해야 한다.

\delta_f=\psi+\tan^{-1}\Big( \frac{ke}{k_s+v_f} \Big)

이렇게 하면 작은 경로 오차에서 과도한 조향각이 발생하는 것을 방지할 수 있다.

Pure Pursuit vs. Stanley

구분	기준점	전방주시거리	고려사항	경로 오차 정의
Pure Pursuit	뒷바퀴 중심	사용	경로 오차	전방주시거리와 경로의 교점에서 차량 축방향까지의 수직거리
Stanley	앞바퀴 중심	사용 안함	경로 오차 + 헤딩 오차	앞바퀴 중심에서 목표경로까지 가장 가까운 거리

두 방법 모두 기구학 기반 경로제어 방법이므로, 차량의 동역학이 발휘되어 타이어 힘이 발생되었을 때는 사용할 수 없다. 따라서 실제 적용하기 위해서는 동역학적 차량 모델 기반 경로제어방법이 필요하다.

Model Predictive Control

MPC는 차량이 앞으로 어떻게 움질일지 예측한 뒤, 그 예측을 바탕으로 최적의 조향각을 결정하는 방법이다. MPC는 다음 세 가지를 동시에 고려한다.

미래의 경로 예측
현재 상황에서 최적의 조향각 선택
차량의 움직임에 대한 제약 조건 고려

MPC는 차량의 움직임을 예측하기 위해 차량 모델이 필요하다. 종-횡방향 힘을 모두 고려한 동역학 기반 차량 모델은 다음과 같은 물리 법칙을 포함하고 있다.

타이어에 작용하는 힘
차량의 회전과 이동
조향각이 차량의 위치와 방향에 미치는 영향 등

하지만, 실제로는 연속적인 시간 흐름이 아니라, 샘플링 타임에 따라 미래를 비선형적으로 나누어서 예측한다. 즉, $t, t+1, t+2, \dots, t+N_p$ 시점까지 조향 각도를 결정한다.

\xi(k+1)=f_\text{dt}(\xi(k),\Delta u(k)), \quad u(k)=u(k-1)+\Delta u(k)

미래 경로를 예측한 후, 그 결과가 얼마나 잘 따라가는지 수치로 평가하는 것을 비용함수라고 한다. 시점 $t$ 에서 $t+N_p$ 까지의 추종 오차와 시점 $t$ 에서 $t+N_c-1$ 까지의 급격한 제어 입력 변화 방지에 대한 합으로 계산된다.

MPC는 현실적인 상황도 반영할 수 있다. 예를 들어,

조향각은 최대 몇 도까지만 돌릴 수 있음
조향 각도 변화 폭은 일정 이상 못 넘김
차량의 속도나 위치도 물리적으로 제한됨

이런 조건을 만족시키면서 비용함수를 최소화하는 방향으로 문제를 푼다.

결국 MPC는 아래와 같은 수학 문제(최적화 문제)로 바뀐다.

\min_{\Delta u(k)}J(\xi,\Delta u) \\ \Delta u^*(t)=[\Delta u(t|t),\cdots\Delta u(t+N_p-1|t)]

이 문제를 실시간으로 계속 풀어서 그 중 가장 첫번째 요소 $\Delta u(t|t)$ 만 차량에 인가되고 나머지 $N_p-1$ 개의 계산된 값들은 사용되지 않는다.

실제로 실험해보면 MPC는 경로를 부드럽고 안정적으로 따라가며 조향각도 부드럽게 변화한다.

장점	단점
미래를 내다보고 최적화	높은 계산량
선형, 비선형 모델 모두 적용	제어기 원리가 직관적이지 않음

다수의 제한조건 동시 고려 가능

차량 횡방향 제어

자동차가 코너를 돌거나 차선을 유지할 때, 차량이 도로 위에서 안정적으로 움지깅기 위해 횡방향 제어가 필요하다. 특히, 미끄러지거나 언더스티어/오버스티어와 같은 위험한 상황을 방지하기 위해서는 안전 제어가 필수적이다. 하지만 차량이 항상 일정한 주행 조건을 유지하진 않기 때문에, 단순한 조향 튜닝으로는 모든 상황에 대응할 수 없다. 이로 인해 Active Control이 필요해졌으며 현재는 이를 ESC라는 이름으로 상용차에 적용하고 있다.

안정성 제어 시스템의 유형

안정성 제어 시스템은 크게 다음 세 가지 방식으로 구분된다.

Differential Braking: 가장 보편적인 방식으로, 오른쪽과 왼쪽 바퀴에 서로 다른 브레이크 압력을 가해 차량의 yaw moment를 조절한다. 예를 들어, 왼쪽 바퀴에 브레이크 압력을 더 많이 걸면 차량이 왼쪽으로 회전하게 된다.
Steer-by-Wire: 운전자의 조향 입력을 전자적으로 감지하고, 보정된 조향각을 바퀴에 전달한다. 기계적인 연결 없이 전기적으로 조향하는 시스템이다.
Active Torque Distribution: 구동력을 네 바퀴에 개별적으로 분배하여 차량의 선회와 안정성을 확보한다. 이 방식은 사륜구동 차량에 주로 적용되며, 코너링 중 휠마다 다른 구동력을 전달해 차량 자세를 유지한다.

제어 시스템 구성도

차량의 횡방향 안정성을 유지하기 위한 제어 시스템은 다양한 센서와 유압/전자 부품으로 구성된다. 예시는 다음과 같다.

차륜 속도 센서: 각 바퀴의 속도를 감지
요레이트 센서/가속도 센서: 차량의 회전 속도 및 측면 가속도 감지
압력 센서 & 하이드로닉 유닛: 브레이크 유압 조절
VDC ECU (Vehicle Dynamics Control Electronic Control Unit): 센서 데이터를 기반으로 제어 명령을 판단하여 브레이크나 엔진 토크 등을 조절

이 시스템은 ESC가 개입할 시 각 바퀴에 개별적으로 브레이크를 적용하거나 엔진 토크를 줄여 차량을 안정적으로 만든다.

안정성 제어를 위해 차량은 다음과 같은 물리량을 실시간으로 측정한다.

Steering angle, Yaw rate, Lateral acceleration, Vehicle speed(휠 센서), Master cylinder pressure

그리고 제어 가능한 항목은 다음과 같다.

Brake pressure, Engine torque(감속용), Steering angle

제어 방식은 크게 두 가지 접근 방식으로 나뉜다.
1. Yaw rate based control: 차량이 회전해야 할 목표 yaw rate와 실제 yaw rate를 비교하여 제어
2. Side slip angle control: 차량이 실제로 얼마나 미끄러지고 있는지를 측정하여 제어

차량 모델

차량의 운동을 설명하기 위해 일반적으로 사용되는 모델은 6 자유도 모델 또는 7 자유도 모델로, 차량의 직선 및 횡방향 움직임, 회전 운동, 각 바퀴의 회전 등을 모두 고려한다.

ESC Using Differential Braking

ESC 시스템과 제어 구조

Electronic Stability Control은 차량이 미끄러지거나 불안정한 상태에 빠졌을 때, 운전자가 원치 않는 방향으로 차량이 회전하지 않도록 도와주는 제어 시스템이다. 이 시스템의 목표는 Yaw Stability Control이다.
상위 제어기는 목표 yaw moment를 계산하고, 하위 제어기는 이를 달성하기 위해 브레이크 제어 입력을 통해 작동한다. 핵심은 빠른 바퀴의 반응을 이용해 느린 차량 동역학을 제어하는 것이다.

Yaw rate based control

목표 yaw rate는 차량의 조향각 $\delta$ 속도 $V$ , 휠베이스 $L$ , 특성속도 $v_\text{char}$ 로 계산된다.

\dot\psi_\text{des}=\frac{v_x}{1+(v_x / v_\text{char})^2}\cdot\frac{\delta_f}{L}

계산된 yaw rate와 센서로 측정된 yaw rate의 오차를 줄이는 방향으로 yaw moment를 생성한다.

장점
- 원하는 yaw rate 계산이 쉽고 명확하다.
- 양산차 관성측정장치에 요레이트 센서가 부착되어 요레이트를 측정할 수 있다.
단점
- 희말 요레이트에 노면에 대한 정보를 포함하지 않아 미끄러운 노면에서 과도한 희망 요레이트를 설정한다.
- 노면 마찰력에 의해 요가 결정되지만 노면 마찰력은 측정하기 어렵다.

Side slip based control

측면 슬립각 $\beta$ 는 차량이 실제 진행 방향과 차체 방향 사이의 각도로, 타이어의 한계 마찰력과 밀접한 관련이 있다.

$\beta$ 가 너무 커지면 타이어가 쉽게 미끄러지며 제어력을 잃는다.
따라서 보통 $\beta$ 를 $\pm5$ 도 이내로 제한한다.

\alpha_f=\beta+\frac{l_f}{v_x}r-\delta_f,\quad\alpha_r=\beta-\frac{l_r}{v_x}r

장점
- 도로 마찰 조건을 완전히 활용할 수 있어 매우 효율적으로 제어할 수 있다.
단점
- $\beta$ 는 직접 측정이 불가능하며 추정이 필요하다.
- 경사로에서는 센서로 측정된 값이 왜곡된다.
- IMU 센서를 이용한 정밀한 추정이 필요하다.

제어 한계 및 안정성 고려

차량은 계산된 yaw rate 또는 $\beta$ 에 항상 도달할 수는 없다. 그 이유는 노면 마찰계수 $\mu$ 에 따라 제어 가능한 최대 가속도가 제한되기 때문이다.
즉, 차량이 도달 가능한 최대 요레이트 및 횡 미끌림 각은 노면 마찰계수에 의해 제한된다.

상위 제어기와 하위 제어기

상위 제어기는 목표 yaw rate와 $\beta$ 값에 따라 슬라이딩 모드 제어기를 구성한다.

차량 모델을 기반으로 슬라이딩 표면을 따라가도록 제어 입력을 설계한다.
필요한 yaw moment를 계산한다.

s=\dot\psi-\dot\psi_\text{target}+\xi(\beta-\beta_\text{target})

하위 제어기에서는 상위 제어기에서 계산한 yaw moment를 실제로 생성하기 위해 좌/우 제동력 차이를 만들어낸다. 그리고 이를 각 바퀴의 브레이크 토크로 변환한다. 바퀴가 감속되며 생성되는 마찰력으로 목표 yaw moment를 유도한다. 마지막으로 패드-디스크 간의 마찰 특성과 거리, 마찰계수 등을 고려하여 토크를 정밀하게 제어한다.

ESC 전체 구조를 요약하자면, 브레이크 토크를 제어하지만 실제 목적은 타이어 마찰력의 제어이다.

고급 횡방향 제어

Friction circle

타이어의 최대 마찰력은 단순히 앞뒤, 좌우 방향 힘으로 나뉘는 것이 아니라 마찰 원이라는 개념으로 표현된다. 이 원은 타이어가 동시에 견딜 수 있는 종방향 힘과 횡방향 힘의 조합 범위를 나타낸다.

예를 들어 가속하면서 동시에 급하게 방향을 바꾸면, 어느 한쪽 방향의 마찰 여유가 부족해지며 미끄러지기 쉽다.
이때 차량의 움직임을 보정하는 요 모멘트를 최소한의 방해로 만들어내는 것이 핵심이다.

Oversteer와 Understeer에서의 보정 전략

오버스티어 상황: 차량이 너무 많이 꺾여 뒷바퀴가 미끄러지는 경우
- 조향보다 차량이 더 돌기 때문에 즉각적인 제어가 필요하다.
- 후륜 구동 차량은 엔진 토크를 줄여 오버스티어를 완화할 수 있다.
언더스티어 상황: 차량이 원하는 만큼 돌지 못하고 외곽으로 밀려나는 경우
- 상대적으로 위험도는 낮고, 제어도 느슨하게 적용된다.
- 전륜 구동 차량은 엔진 토크를 줄여 앞바퀴의 조향력을 확보한다.

실용적인 문제들

제어 모멘트를 만들기 위해 사용되는 제동 토크는 브레이크 압력에 의존하지만, 대부분의 차량은 실제 브레이크 압력을 직접 측정하지 않는다.
대신 밸브 명령값과 공급 압력을 통해 추정하며, 정확도가 떨어질 수 있다.
과도한 제동은 바퀴를 잠그거나, 불안정한 마찰 및 슬립 구간에 진입시켜 제어를 어렵게 만든다.
- 슬립 컨트롤러와 병행하여 적절한 슬립 범위 내에서 제어가 필요하다.

따라서 실 차량에서는 요 레이트 기반 제어와 사이드 슬립 기반 제어를 혼합하여 사용한다. (실제로는 요 레이트 기반 제어가 흔히 사용된다.)

설계 시 다음의 사항을 고려해야 한다.

과도한 브레이크 개입은 매우 위험하기 때문에 약간 느슨한 제어가 오히려 안정적일 수 있다.
조향 입력이 갑자기 발생하는 순간, 앞바퀴 슬립각 $\alpha_f$ 가 커지며 일시적으로 언더스티어로 오해될 수 있으므로, 실제로는 제어가 필요 없는 상황일 수도 있다.
브레이크나 엔진 토크 제어는 차량 속도를 줄이기 때문에 정말 필요한 상황에서만 사용해야 한다.

고급 기능

Active Steering
- BMW가 2003년 개발한 능동 조향 시스템은 차량의 속도에 따라 조향각을 자동 조정해준다.
- 주차 등 저속 주행 시 민첩한 움직임을 위해 조향각을 더 많이 부여하고 (큰 조향비), 고속 주행 시 차량의 안정성을 확보하기 위해 조향각을 줄인다. (작은 조향비)
Damping
- CDC (Continuous Damping Control): 노면 상태나 차량 움직임에 따라 감쇠력을 능동적으로 조절
- Active Roll Control: 롤링 억제를 위해 롤 바를 능동적으로 조작하여 코너링 시 차량 안정성 확보
Torque Distribution
- 각 바퀴 또는 앞/뒤 구동축에 정밀하게 토크를 분배하는 시스템으로, 트랙션 확보와 요 안정성 향상에 효과적
- 단, 매우 고가 시스템이기 때문에 비용 대비 효과 분석이 필요하다.

다양한 4WD 시스템

4륜구동은 단순히 네 바퀴가 굴러가는 것이 아니라, 구동 방식에 따라 다음과 같이 나뉜다.

Full-time 4WD: 항상 네 바퀴에 구동력 제공
Part-time 4WD: 필요시 2WD와 4WD 모드 전환 가능
Automatic 4WD: 보통은 2WD로 주행하다가 필요시 자동으로 4WD로 전환

4WD는 제동력을 증가시키지 않고, 건조한 노면에서는 오히려 제동이 더 어려울 수 있다.

Kinematic Model 기반의 차량 횡방향 제어

Kinematic Model을 쓰는 이유

기구학적 모델은 차량을 단순화하여 물리적인 힘보다는 기하학적인 관계로만 차량 움직임을 설명하는 모델이다.

실제 차량은 복잡한 힘, 마찰, 슬립 등의 동역학이 작용하지만,
저속이거나 정밀한 위치 제어가 필요한 경우에는 이런 복잡한 요소 없이도 기하학적 관계만으로 제어가 가능하다.

그래서 저속 후진 주차나 정밀 주행 같은 상황에서는 Kinematic Model 기반 제어가 효율적이고 직관적이다.

기본 구성: Kinematic Bicycle Model

차량을 자전거 형태의 모델로 단순화 한다.

차량은 앞바퀴 한 쌍, 뒷바퀴 한 쌍이 있는 것처럼 구성된다.
조향은 앞 바퀴만, 추진력은 뒷바퀴만으로 가정한다.
상태 변수는 다음과 같다.
- $x, y$ : 차량의 위치
- $\theta$ : 차량이 바라보는 방향 (yaw)
- $v$ : 속도
- $\delta$ : 조향각

궤적 추종 제어

차량이 도로 중심선이나 목표 경로를 따라가게 만들기 위해 두 가지 오차를 정의한다.

측방 거리 오차: 차량이 경로에서 얼마나 떨어져 있는지
방향 오차: 차량이 경로 방향에서 얼마나 기울어져 있는지

이 두 오차를 최소화하는 방향으로 조향각을 조정한다.

제어 입력 $u$ 는 조향각 $\delta$ 에 해당하며, 궤적 오차에 따라 다음과 같이 정의한다.

u=-k_1e_1-k_2e_2

여기에서 $k_1,k_2$ 는 오차에 대한 민감도를 조절하는 제어 gain이며, 이 값에 따라 차량이 경로에 얼마나 빠르게 복귀할지 결정된다.
또는 Feedback Linearization 기법을 통해 비선형 시스템을 선형처럼 바꿔 제어할 수도 있다.

‍이세현

Hi, there 👋

이전 포스트