Overfitting Regularization

딥러닝 네트워크 층이 많이 쌓이고 각 층의 노드 개수가 많아질수록 네트워크를 구성하는 가중치 개수가 더 많아지고 네트워크의 표현력(capacity)이 높아진다. 모델을 학습시킬 데이터가 한정된 상황에서 capacity가 높을수록 모델은 학습 데이터에 fitting이 더 잘 되어 training error는 떨어지지만 test error는 커진다.

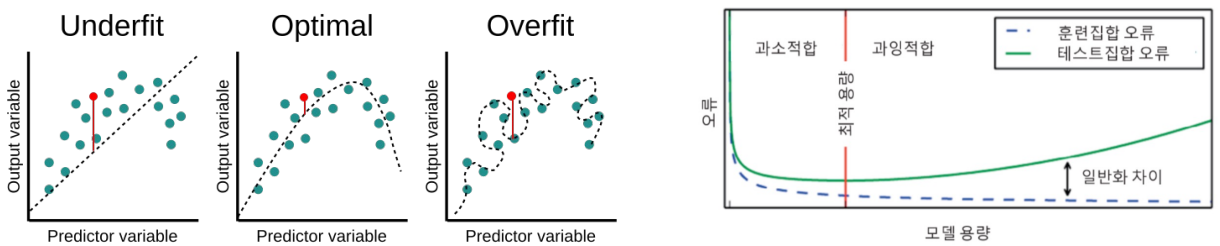
Model capacity가 큰 딥러닝 모델에서 과적합을 방지하는 방법으로 early stopping, weight decay, data augmentation, dropout, batch narmalization이 있다.

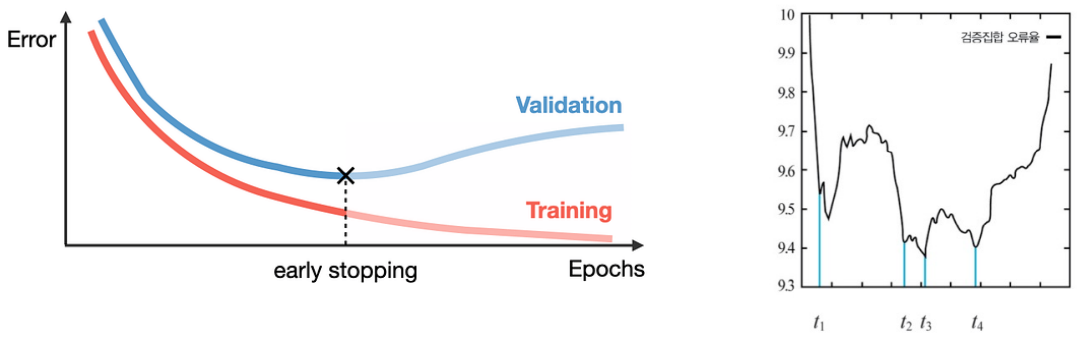
Early Stopping

Validation set에 대한 error가 더이상 감소하지 않고 정체되어 있거나 증가하는 경우 학습을 조기 종료한다.

• 일부 기간 종료하지 않고 기다리면 error가 다시 감소할 수 있다. 어느 정도 지켜보다가 validation error가 감소하지 않으면 그때 학습을 조기에 종료하는 방법(tolerance)도 있다.

Weight Decay

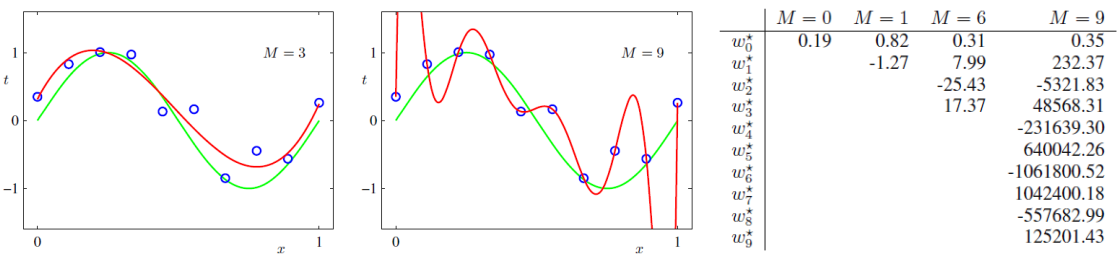
• 다항식 fitting의 예(차수가 $\mathbf{M}$일 때)

  $y(x, \mathbf{w})=w_0+w_1x+w_2x^2+\cdots+w_\mathbf{M}x^\mathbf{M}=\sum_{j=0}^{\mathbf{M}}w_jx_j$
  • Overfitting된 모델은 가중치의 값이 매우 크다.
  • 각 가중치가 큰 값을 가지지 못하도록 penalty를 부여하여 가중치 값을 감쇠시킬 수 있다.
    • $\lambda$를 키워 규제의 강도를 높인다.
  1. Lasso Norm (L1 Norm)
     $E=\frac{1}{2}\times\sum(t_k-o_k)^2+\lambda\times\sum\|w_i\|$
     • 가중치 값을 0으로 만들기 때문에 가중치 값이 크면 수렴 속도가 느리다.
     • 중요한 특징을 선택하는 효과
     • 모델에 Sparsity를 가한다.
     • 미분하면 $-1$ 또는 $+1$
  2. Ridge Norm (L2 Norm)
     $E=\frac{1}{2}\times\sum(t_k-o_k)^2+\frac{\lambda}{2}\times\sum\|w_i\|^2$
     • 가중치 크기에 비례하여 큰 가중치 값을 작게 만든다.
     • 모델 전반적인 복잡도를 줄이는 효과
     • 가중치의 값이 0이 되게 하지는 못한다.
     • 미분하면 $\mathbf{w}$

Data Augmentation

데이터가 많으면 모델이 쉽게 과적합되지 않는다. 모델의 구조, 손실과 무관하게 데이터의 양을 최대한 늘리면 과적합을 피할 수 있다.

• 데이터를 늘리는 (효과를 만드는) 방법
  1. 개별 이미지 데이터 안에서의 증강
     • Flip: 좌우 반전
     • Rotation: 기울기
     • Random Crop: 확대, 자르기
     • Color Shift: 색 조절
     • Noise Addition: Gaussian 등 잡음 추가
     • Information Loss: 이미지 일부분에 마스킹
     • Contrast Change: 명도, 채도 조절
     • 증강법은 데이터의 특성에 맞게 사용해야 한다.
  2. 미니배치 안의 여러 데이터를 사용하는 증강
     • Mixup: 두 이미지의 투명도를 조절해서 하나의 이미지로 결합
     • CutMix: 두 이미지를 잘라서 결합
       

Drop Out

학습 과정에서 신경망의 노드 일부를 drop out 하여서 drop out 된 노드에 연결된 가중치를 사용하지 않는 방법

• Hyperparameter: Drop probability $p$
  • 일반적으로 0.5를 가장 많이 사용한다.
• 매 반복마다 개별적으로 dropout을 적용하여 매번 다른 노드, 다른 가중치를 가지고 학습을 수행한다.
  • 데이터 암기를 방지하여 과적합을 막는 효과
    
• 평가 시에는 드롭아웃된 노드 없이 신경망의 모든 노드를 사용한다. 훈련 시 사용한 노드 개수보다 많으므로 평가할 때 노드 출력값은 커질 수밖에 없다. 따라서 평가 때는 각 뉴런의 출력에 $1-p$를 곱해주어야 한다.

Batch Normalization

• Internal Covariate Shift: 매 반복(미니배치)마다 은닉층에 들어오는 input 데이터의 분포가 달라진다.
  • 깊은 layer일수록 이 현상이 더 심해진다.
• 미니배치 내 각 데이터에 대해 평균을 빼고 분산으로 나누어 평균 0, 분산 1의 정규분포로 변환한다.
  $x_i^\text{new}=\frac{x_i^\text{old}-\mu_i}{\sigma_i}$
  • 활성함수 적용 전 중간 값 $Z$에 대해 정규화를 수행한다.
  • 정규화 변환값을 선형변환한다.
    $z_i'=\gamma{z_i}+\beta_i$
    • ReLU 비선형함수를 사용할 경우 정규화된 데이터 절반은 음수이기 때문에 0으로 죽어버리는 문제가 있다. Sigmoid 비선형함수를 사용할 경우에는 정규화된 데이터 대부분 세로축 가까이에 분포하기 때문에 비선형 역할을 수행하지 못하는 문제가 있다. 따라서 정규화된 데이터를 선형변환을 거쳐 활성화 함수에 입력한다.
    • $\gamma$와 $\beta$는 각 노드마다 다른 값으로, 역전파를 통해 학습된다.
• Regularization 효과
  • Internal Covariate Shift 해소로 인해 깊은 층에서 학습이 보다 더 잘 이루어진다. 모델이 얕은 층에서의 feature를 과도하게 의존하고 암기하는 것을 방지하여 간접적인 regularization 효과가 나타난다.
• 평가 시에는 배치 단위의 평균과 분산을 구할 수 없다. 따라서 학습 단계에서 moving average, exponential average를 이용하여 계산한 평균과 분산을 고정값으로 사용하여 평가한다.