Variational Auto-Encoder

Autoencoder + 확률

Auto-Encoding Variational Bayes

Autoencoder v.s. Variational Auto-Encoder

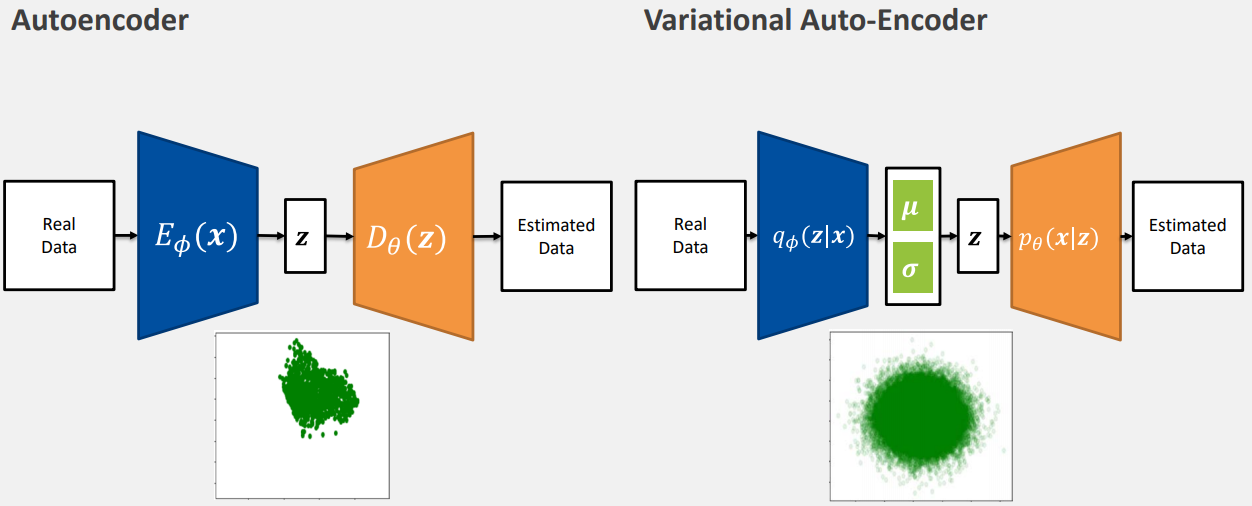
• Autoencoder
  • latent space에 임의의 값을 넣었을 때 decoding 후 의미있는 값이 나와야 한다.
  • image data 하나를 나타내는 vector인 latent space의 분포가 고르지 않다.
    • 초기화에 따라 학습 이후의 latent space 분포 모양이 달라진다.
    • sampling을 고르게 할 수 없으며 sampling 시 sampling에 대한 정보도 필요하다.
• Variational Auto-Encoder
  • random value를 유발하는 parameters인 $\mu$와 $\sigma$를 포함한다.
  • $\mu$와 $\sigma$를 통해 latent를 원하는 모양(정규분포)으로 분포시킬 수 있다.

Variational Auto-Encoder (VAE)

• variational bayes를 기반으로 하는 auto-encoder
  • 확률분포의 parameter를 최적화한다.
• Encoder model: $q_\phi(\mathbf{z}|\mathbf{x})$
  • $\mathbf{x}$: 입력 이미지
  • $\mathbf{z}$: latent space
• Decoder model: $p_\theta(\mathbf{x}|\mathbf{z})$
• Optimization
  • $\mathcal{L}(\phi, \theta, x)=(\text{recon.loss}+\text{reg.loss})$
  • Reconstruncion loss
    $\|x-\hat{x}\|^2$
  • Regularization(인간의 가정) loss: divergence
    $D\big(q_\phi(z|x) \| p(z) \big)$
    $x$가 주어졌을 때 encoder $q_\phi$는 latent $z$의 분포가 정규분포 $p(z)$(prior)에 가까워지도록 학습을 진행한다.

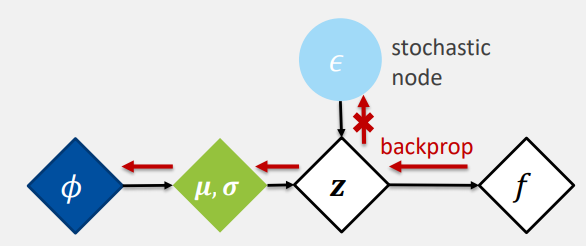
Reparameterization Trick

• Encoder $q_\phi(z|x)$가 고정된 prior 분포 $p(z)$와 유사하게 latent space에 고르게 분포하도록 해야한다.

ex) $p(z)$를 정규분포로 고정하였을 때

ex) 표본화된 latent vector $z \sim p(z)$를 $\mu$와 $\sigma$의 합으로 간주하고, 임의의 상수 $\epsilon$에 의해 scale한다.

• $z$는 $\mu$와 $\sigma$로 구성하거나 완전 random 값으로 구성할 수 있다.

  • random value는 학습할 수 없다.
  • $z=\mu+\sigma \odot\epsilon$

• 연산 구조로 만들면 back propagation이 가능해진다.

  • $\mu$: latent space에서의 평균을 나타내는 변수로, encoder network 입력 $x$로부터 추정한다.

  • $\sigma$:latent space에서의 표준 편차를 나타내는 변수로, encoder network가 입력 $x$로부터 추정한다.

  • $\epsilon$: 표준 정규 분포(즉, 평균 0, 분산 1)에서 샘플링된 노이즈 변수

    • 무작위로 생성되어 확률적 요소를 제공한다.
    • 일반화 능력과 유연성에 도움이 된다.
    • 입력 데이터로부터 도출된 평균 $\mu$와 표준 편차 $\sigma$에 기초하여 latent $z$를 간접적으로 생성한다.
    • 확률적인 요소는 모델의 학습 과정 중에 gradient 계산과 back propagation에 영향을 미치지 않으면서도 모델이 데이터의 확률적 특성을 학습할 수 있도록 한다.
      

  • $\odot$: 요소별 곱셈(element-wise multiplication)

    • $\sigma$와 $\epsilon$ 각각의 요소를 요소별로 곱한다.

  • loss를 최소화하는 과정
    $p_\theta(x|z)$ back propagation
    $\rightarrow \theta$ update
    $\rightarrow z$가 잘 나와야 하므로 $\mu$와 $\sigma$ 학습
    $\rightarrow \phi$가 잘 나와야함

  • 부드러운 sample 분포
    

Conditional VAE

• 조건적 확률을 encoder와 decoder에 입력과 같이 부여한다.
  • Encoder $q_\phi(z|x,c)$
  • Decoder $p_\theta(x|z,c)$
• Neural network 구조에 따라 $c$의 입력 방식이 달라진다.
  • Linear layer이면 $c$를 입력 vector에 concatenate
  • Convolution layer이면 one-hot encoded $c$를 input image channel에 추가한다.