Vision Linear Model

Machine Learning: Linear Classifiers

CIFAR-10 Dataset

• $32\times32\times3$ 크기의 50,000 학습 이미지와 10,000 테스트 이미지로 이루어진다.
• Training set으로 테스트하면 정확도가 높을 수밖에 없으므로 학습에 사용하지 않는 Test set을 별도로 두어야 한다.

Parametric Approach

• $x$: $[32\times32\times3]$ 크기의 숫자로 이루어진 이미지
• $W$: Parameter, weights로 바뀔 수 있는 값
• $f(x,W)$: 각 클래스에 해당하는 확률 값 벡터
• Shape: $[10,]=[10,3072]\times[3072,]$
  • Matrix인 $W$와 $x$의 곱은 벡터 간 내적의 반복이다.
  • 내적: 선형 연산(정사영)으로, 두 벡터가 유사할수록 높은 값을 가진다.

---

• $b$: bias로, 데이터가 편향되어 분포되어 있어도 표현력을 유지하는 방법
• Shape: $[10,]=[10,3072]\times[3072,]+[10,]$

Example for $2\times2$ image, 3 classes

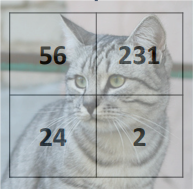
1. Input image의 Pixel 값을 column vector로 펼친다.
   • 
   • $(2,2)\rightarrow(4,)$
   • 일반화: $(H,W)\rightarrow(H\times W,)$
2. 각 클래스를 대변하는 값(weight)와 픽셀 벡터를 곱한다. 이후 Bias를 더한다.
   • 
   • $(3,4)\times(4,)+(3,)=(3,)$
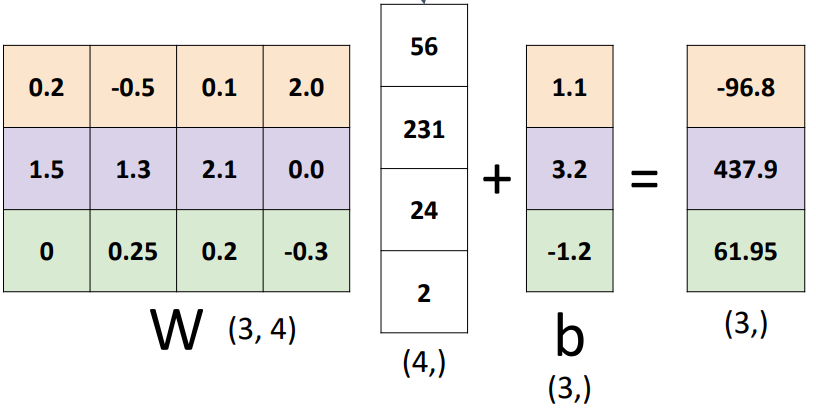
   • 일반화: $(\text{Class},H\times W)\times(H\times W,)+(\text{Class},)=(\text{Class},)$
   • Bias를 더하는 과정은 동차를 활용하여 단순화할 수 있다.
     • 
     • $(3,5)\times(5,)=(3,)$
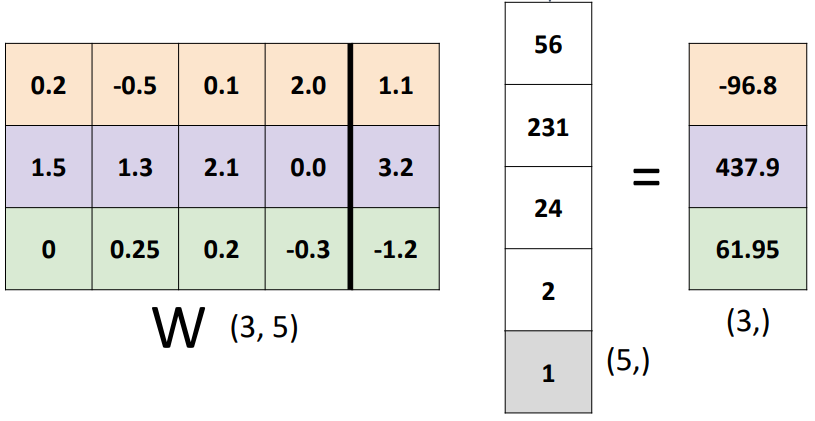
     • 일반화: $(\text{Class},H\times W+1)\times(H\times W+1,)=(\text{Class},)$
   • 가중치를 구성하는 Row Vector 각각은 class를 대변하는 값이기 때문에 서로 독립적이고 영향을 끼치지 않는다.

Interpreting a Linear Classifier

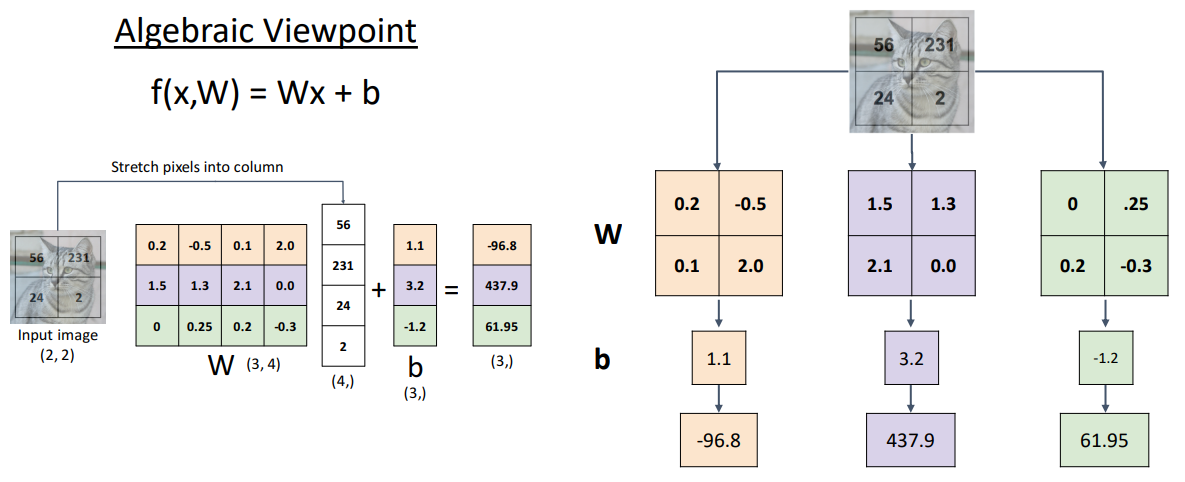
$(H, W)$ 크기의 이미지를 벡터로 펼치지 않고 weight를 이미지 형태로 바꾸어 연산할 수 있다.

• $(\text{Class},H\times W)$ 형태의 weight를 $(H,W)$ 크기의 weight $\text{Class}$ 개수 만큼 만들어 element-wise로 곱하고 더하면 벡터 내적 연산과 동일하다.
  • 이를 Template Matching이라고 한다.
• $(\text{Class},)$ 형태의 출력 벡터에서 가장 큰 값에 해당하는 class가 predict 값이 된다.
• 학습이 완료된 template를 출력하면 각 클래스에 해당하는 이미지의 평균값이 나타난다.
  • 
  • 각 클래스에 해당하는 template은 단 하나이므로, 모든 형태의 데이터를 표현할 수 없다. 하나의 template이 해당 클래스의 모든 데이터를 나타내기 때문이다.
    • 'Horse' Template의 경우 두 개의 머리가 두드러진다.
    • Linear 모델의 한계: 복잡한 데이터를 표현할 수 없다. (XOR 문제와 동일)

Score Function

• 모델의 출력이 최선이 출력인지, 그렇지 않은지 판별하고 최적의 가중치를 선택하는 방법
  1. Loss function을 이용하여 최적의 가중치인지 확인한다.
  2. Loss function 값을 최소화하는 가중치를 찾아간다. (최적화, 학습)
• Loss function: 모델이 얼마나 좋은 성능인지 나타낸다.
  • 하나의 샘플에 대한 손실: $L_i(f(x_i,W),y_i)$
    $L=\frac{1}{N}\sum_i L_i(f(x_i,W),y_i)$
• Cross-Entropy Loss
  • 고양이 이미지에 대한 Linear Model의 출력이 cat 3.2, car 5.1, frog -1.7일 때
  • 최종 출력은 확률로 나타나야 한다.
    • scalar 값을 확률로 바꾸는 대표적인 방법으로는 softmax function이 있다.
    • $P(Y=k|X=x_i)=\frac{\exp(s_k)}{\sum_j\exp(s_j)}$
    • 이때 $s_k$는 $k$ 클래스에 해당하는 모델 출력
    • $s_k$의 합은 1이어야 한다.

    • class	output	$\exp$	softmax
      cat	3.2	24.5	0.13
      car	5.1	164.0	0.87
      frog	-1.7	0.18	0.00

  • 최종 Loss
    • cat label의 경우 softmax 함수의 출력이 1에 가까울수록 손실이 적어야 한다. 반면 0에 가까울수록 손실이 커야 한다.
    • $-\log P(Y=y_i|X=x_i)$
    • $-\log(0.13)=2.04$, 0에 가까울수록 loss는 기하급수적으로 커진다.
    • 모델은 cat에 대한 예측 확률이 1에 가까워지도록 학습된다.