Convolution Neural Network

Image 처리에서 MLP의 한계

1. 이미지를 1차원 벡터로 flatten하며 2차원 spatial 정보가 손실된다.
   • 예) MNIST $[1, 28, 28] \rightarrow [784]$

     x = x.view(-1, 28*28)

2. Linear layer에서는 모든 node가 연결되어 있어 image 내 물체의 위치에 따라 다른 결과가 도출된다.
   • Fully Connected Layer의 한계
   • 동일한 배경의 사물이 오른쪽으로 두 픽셀 이동하여도 node 연결은 동일하기 때문에 비효율적이다.
3. Fully Connected Layer이므로 매우 많은 가중치가 필요하다.
   • 이미지 너비나 높이에 따라 데이터 사이즈는 그의 제곱만큼 증가한다.
   • Overfitting에 취약하다.
   • 예) 은닉층 노드 개수가 10일 때 $[32\times32]$ 이미지를 입력으로 받는 가중치 개수는 $(32\times32\times3)\times10=30720$
   • 예) 은닉층 노드 개수가 10일 때 $[1024\times1024]$ 이미지를 입력으로 받는 가중치 개수는 $(1024\times1024\times3)\times10=31457280$

CNN

• Convolution $\sim=$ sliding window $\sim=$ tensor 내적
  • 
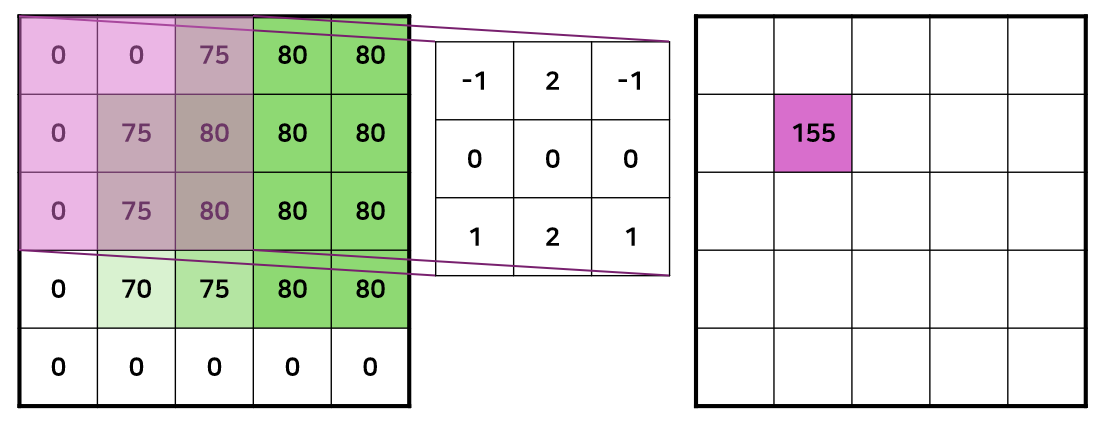
  • 필터를 움직이며 이미지와 element-wise로 곱한다.
    • $155=-75+150+80$
    • Filter는 가중치들로 이루어져있어 gradient descent를 통해 학습시키는 것이 목표이다.
    • Bias 값도 있으므로 위의 예에서 총 weight 개수는 10개이다.
• 딥러닝 이전 고전 컴퓨터 비전 분야에서 이미지 처리를 위해 사람이 설계한 필터로 컨볼루션 연산을 사용했었다.
  • 딥러닝을 통해 데이터로 컨볼루션 필터를 학습시키는 과정으로 이어졌다.
• MLP vs CNN
  1. Flatten 과정이 없으므로 이미지 spatial 정보는 유지된다.
  2. 필터가 움직이며 이미지 정보를 확인하므로 물체 위치에 상관 없이 동일한 결과 도출
  3. Image 수와 무관한 filter(weight) 크기

CNN의 구성

• in_channels: 입력 이미지의 channel 수
• out_channels: filter의 개수
• kernel_size: 필터 크기를 나타내는 scalar. 일반적으로 정사각형 filter를 사용한다.
• stride: default 값은 1
• padding: 출력값의 spatial size가 작아지지 않도록 하는 역할
• pooling: 이미지 사이즈를 줄여 CNN 가중치 개수를 줄이고 overfitting을 억제하는 역할
  • 한 뉴런 활성화에 기여하는 입력 이미지의 영역인 Receptive field를 늘려준다.
  • Pooling layer는 레이어 개수에 포함되지 않는다.
• Fully connected layer: 모든 feature를 기반으로 최종 prediction을 수행
  • 마지막 과정에서는 flatten이 필요하다.