딥러닝 모델 학습과 가중치 업데이트 과정
딥러닝 모델은 입력값을 받아 순전파를 통해 예측값을 계산하고 예측값과 실제값의 차이를 손실 함수를 통해 구한다. 그 후 이 손실을 기반으로 역전파를 통해 각 가중치가 얼마나 잘못되었는지를 계산하여 가중치를 수정한다. 이 글에서는 순전파(Forward Propagation)와 역전파(Back Propagation)의 과정을 알아본다.
1. 순전파(Forward Propagation)
1.1 순전파란?
딥러닝의 순전파는 입력층에서 출력층까지의 계산을 순차적으로 수행하며 중간 연산 결과를 저장하는 과정을 말한다. 이 과정에서 각 층의 가중치(W)와 편향(b)으로 연산을 진행한다. 이 글에서는 편향(b)를 고려하지 않고 계산한다.
1.2 예제 네트워크 구조
직접 계산해보기 편하게 아주 간단하게 구성했다.

1.3 순전파 계산 과정
활성화 함수는 시그모이드 함수를 사용한다. 활성화 함수 공부글 보러가기
z1=w1⋅x1=0.3×0.1
h1=Sigmoid(z1)
z2=w2⋅h1=0.45×0.57=0.25
o1=Sigmoid(z2)=0.56
E=MSE=(y−o1)2=(0.4−0.56)2=0.0256
y = 실제값
2. 역전파(Back Propagation)
2.1 역전파란?
역전파는 순전파의 과정을 역행한다. 순전파에서 계산된 오차(loss)를 기반으로 손실 함수의 기울기(gradient)를 계산하여 손실 함수의 값이 최소화되도록 가중치를 업데이트하는 역할을 한다.
2.2 역전파 계산과정
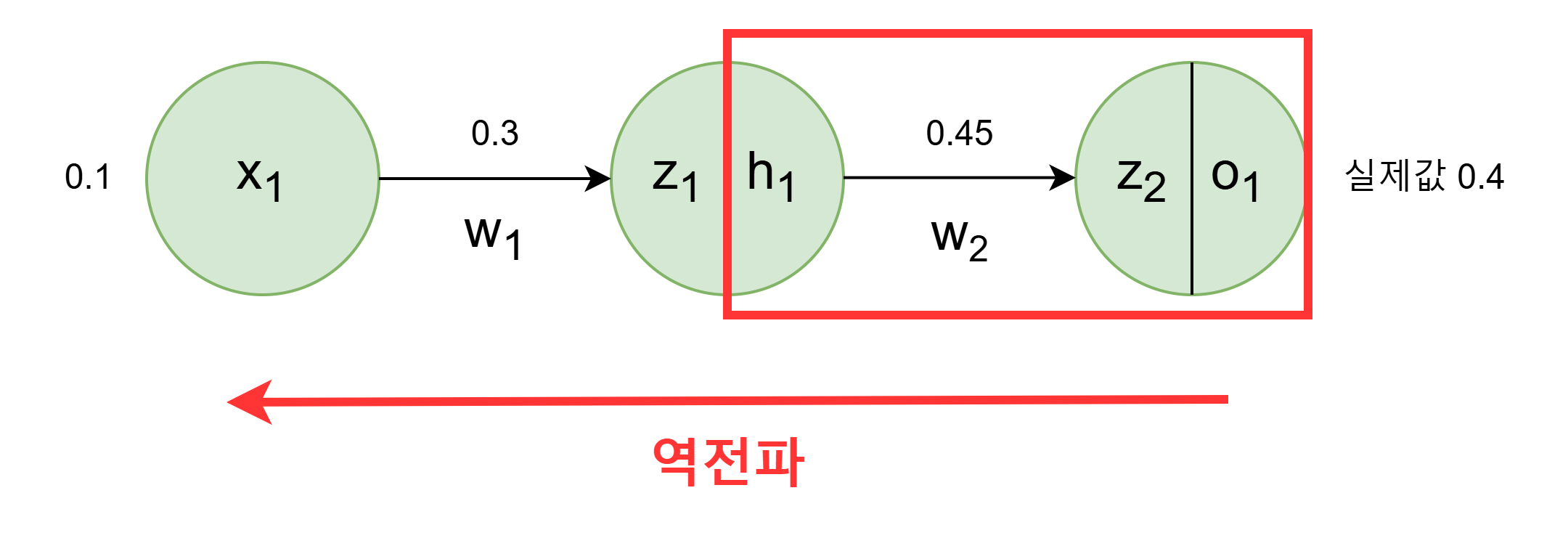
2.3 w2 가중치 업데이트
경사하강법 (w2=w2−lr⋅∂w2∂E) 을 사용하려면 ∂w2∂E 값을 알아야한다.
∂w2∂E는 체인 룰(미분의 연쇄 법칙)에 따라 다음과 같이 풀어쓸 수 있다. 이제 각 항의 값을 계산하여 곱한다.
∂w2∂E=∂o1∂E⋅∂z2∂o1⋅∂w2∂z2
∂o1∂E=2(y−o1)2−1×−1+0=2×−0.16=−0.32
o1는 시그모이드 함수의 출력값이다. 시그모이드 함수의 미분은 f(x)=f(x)⋅(1−f(x))이다.
∂z2∂o1=o1⋅(1−o1)=0.56×0.44=0.24
∂w2∂z2=h1=0.57
∂w2∂E=−0.32×0.24×0.57=−0.043776
이제 경사하강법을 통해 가중치 w2를 업데이트 할 수 있다.
w2=w2−lr⋅∂w2∂E=0.45−0.5×−0.043776=0.471888
2.4 w1 가중치 업데이트
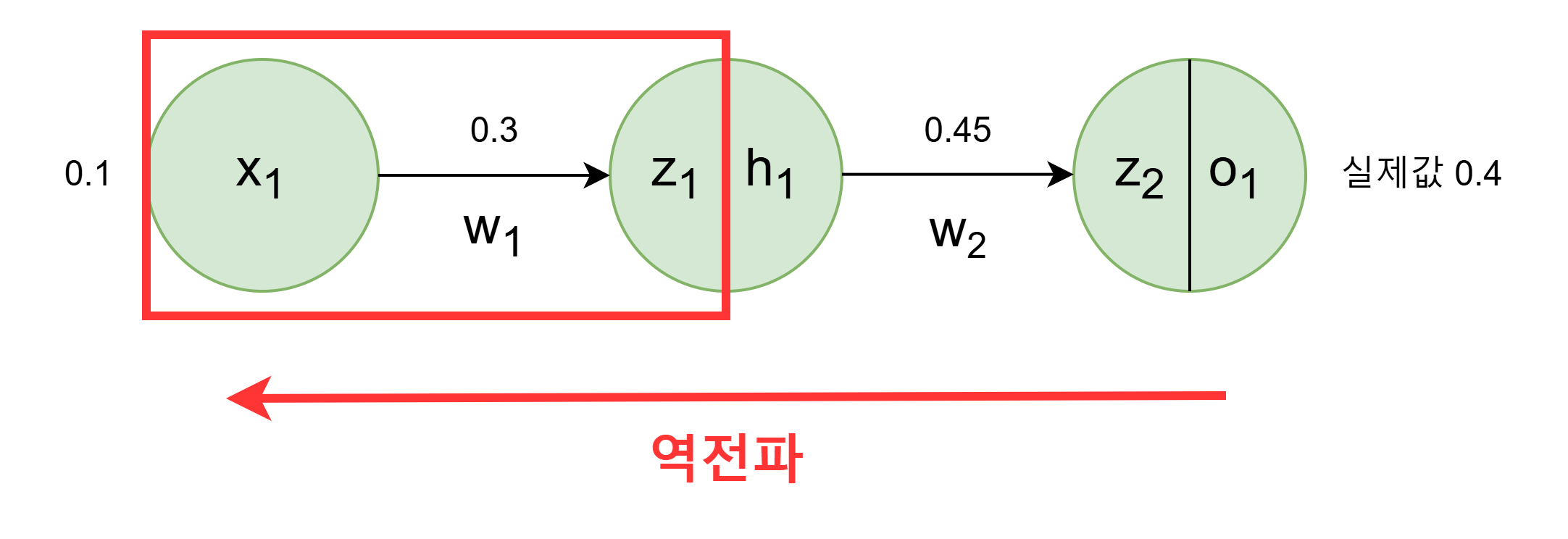
w1역시 경사하강법 (w1=w1−lr⋅∂w1∂E) 을 사용하려면 ∂w1∂E 값을 알아야한다.
∂w1∂E는 체인 룰(미분의 연쇄 법칙)에 따라 다음과 같이 풀어쓸 수 있다.
∂w1∂E=∂h1∂E⋅∂z1∂h1⋅∂w1∂z1
이제 다시 각 항의 값을 계산한다.
∂h1∂E는 체인 룰에 따라 다음과 같이 풀어쓸 수 있다.
∂h1∂E=∂z2∂E⋅∂h1∂z2
∂z2∂E는 체인 룰에 따라 다시 다음과 같이 풀어쓸 수 있다.
∂z2∂E=∂o1∂E⋅∂z2∂o1
결론적으로 ∂h1∂E는 다음과 같다.
∂z2∂E=∂o1∂E⋅∂z2∂o1⋅∂h1∂z2
이때 ∂h1∂z2는 w2이다. 마지막으로 계산해보면 다음과 같다.
∂z2∂E=−0.32×0.24×0.42=−0.03456
다음으로 ∂z1∂h1의 값을 계산한다.
∂z1∂h1=h1⋅(1−h1)=0.57×0.43=0.2451
∂w1∂z1는 x1이다.
∂w1∂z1=0.1
∂w1∂E=−0.3456×0.2451×0.1=−0.008470656
이제 경사하강법을 통해 가중치 w1을 업데이트 할 수 있다.
w1=w1−lr⋅∂w1∂E=0.3−0.5×−0.008470656=0.3004235
3. 결과 확인
3.1 업데이트 된 가중치 확인
업데이트 한 가중치를 적용하여 계산해서 오차(loss)가 줄었는지 확인한다.
w1 : 0.3 👉 0.304235328
w2 : 0.45 👉 0.471888
3.2 순전파 다시 진행
z1=w1⋅x1=0.304235328×0.1=0.0304235328
h1=Sigmoid(z1)=0.507605
z2=w2⋅h1=0.471888×0.507605=0.23953270824
o1=Sigmoid(z2)=0.559598
E=MSE=(y−o1)2=(0.4−0.559598)2=0.025471521604
y = 실제값
3.3 결과
업데이트 전 오차는 0.0256 이었는데 가중치 업데이트 후 오차는 0.0254 이다. 미세하지만 줄은 것을 확인했다.
4. 마무리
이번 글에서는 딥러닝 모델의 학습 과정 순전파와 역전파의 원리를 직접 계산해보며 자세히 알아보았다. 미세한 변화가 반복되면서 결국 모델의 성능은 향상된다. 나도 작은 변화를 통해 더 나은 사람이 되어야겠다.
5. 레퍼런스




