어텐션 메커니즘(Attention Mechanism)

현주·2024년 12월 31일

어텐션 메커니즘이란?

이전글에서 정리한 seq2seq 모델은 두가지 문제가 있다.

하나의 고정된 크기의 벡터에 모든 정보를 압축하려니 정보 손실이 발생한다
RNN의 고질적 문제, 기울기 손실 문제

이는 입력 문장이 길어지면 성능이 떨어지게 된다. 이를 보완하기 위해 어텐션 기법이 등장했지만, 어텐션 스스로가 seq2seq를 대체하는 방법이 되어간다.

어텐션의 기본 아이디어는 디코더에서 출력 단어를 예측하는 매 시점에서 전체 입력문장을 다시 참고한다는 것이다.
여기서 참고할 때 해당 시점에서 예측해야 할 단어와 연관있는 부분을 더 집중(어텐션)해서 참고하게 된다.

어텐션 함수

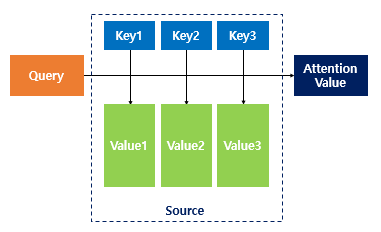
어텐션 함수를 표현하면 다음과 같다.
$Attention(Q, K, V) = Attention Value$

Q = Query : t 시점의 디코더 셀에서의 은닉 상태
K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
V = Values : 모든 시점의 인코더 셀의 은닉 상태들

어텐션 함수는 주어진 쿼리(Query)에 대해 모든 키(Key)와의 유사도를 각각 구한다.
그리고 구한 유사도를 키와 맵핑된 값(Value)에 반영한다.
그리고 유사도가 반영된 값을 모두 더해 리턴한다. 이 값을 어텐션 값이라고 하겠다.

어텐션은 다양한 종류가 있지만, 수식을 적용한 닷 프로덕트 어텐션을 통해 어텐션을 더 알아보자.

닷-프로덕트 어텐션(Dot-Product Attention)

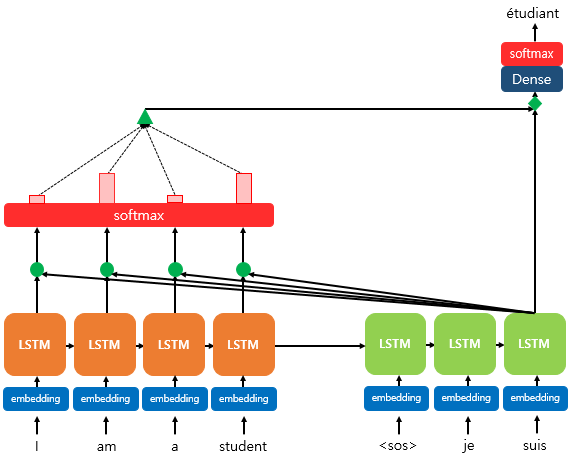
위 그림은 디코더의 세번째 셀에서 단어를 예측할 때 어텐션 메커니즘을 사용하는 모습이다. 디코더의 앞의 두 셀은 이미 어텐션 메커니즘을 통해 예측하는 과정을 거쳤다고 가정한다.

디코더의 세번째 셀은 다음 단어를 예측하기 위해 인코더의 전체 단어의 정보를 다시 참고하려한다.

소프트맥스 함수를 통해 나온 결과는 각 단어가 디코더에서 예측할 때 도움이 되는 정도를 수치화한 값이다. 이 값을 하나의 정보로 담아서 디코더로 전달된다.

디코더의 현재시점 t에서 필요한 정보는 이전 시점의 출력 단어와 은닉 상태다.
그런데 어텐션 메커니즘에서는 하나가 더 필요하다. 바로 어텐션 값(Attention Value) $a_t$ 이다.

어텐션 값을 구하기 위해서는 어텐션 스코어(Attention Score)를 구해야 한다.

어텐션 스코어

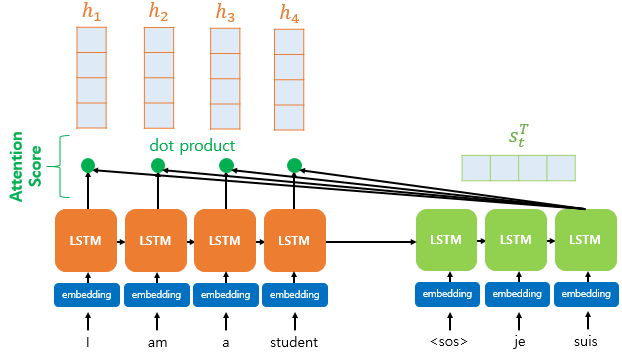
어텐션 스코어란 현재 시점 t에서 인코더의 모든 은닉상태 각각이 디코더의 현재 시점 은닉상태 $s_t$ 와 얼마나 유사한지 판단하는 점수이다.

닷 프로덕트 어텐션에서는 어텐션 스코어를 구하기 위해 현상태의 은닉 상태 $s_t$ 를 전치하여 각 은닉 상태와 내적(dot product)한다.

어텐션 스코어 함수의 수식을 정리하면 다음과 같다.

score(s_t, h_i) = s^T_th_i

어텐션 스코어의 모음값을 $e^t$ 라고 정의했을때 수식은 다음과 같다.

e^t = [s^t_t h1,...,s_t^Th_N]

어텐션 분포

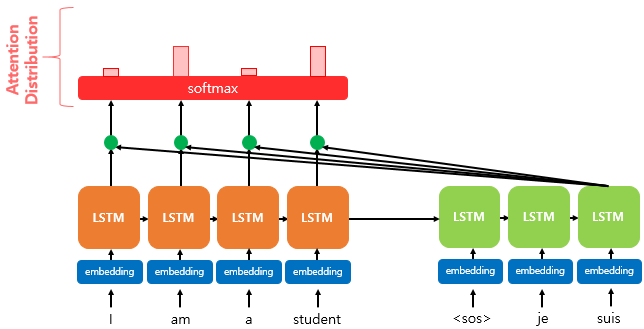
어텐션 스코어의 모음인 $e^t$ 에 소프트맥스 함수를 적용해 모든 값을 합하면 1이 되는 확률 분포를 얻는다.

이를 어텐션 분포(Attention Distribution)라고 하고, 각각의 값은 어텐션 가중치(Attention Weight)라고 한다.

\alpha^t = softmax(e^t)

어텐션 값

이제 구한 값들을 하나로 합친다. 각 인코더의 은닉상태와 어텐션 가중치들을 곱하고 모두 더한다.

이런 어텐션 값은 인코더의 문맥을 포함하고 있다는 의미에서 컨텍스트 벡터라고도 불린다.

a_t = \sum^N _{i=1} \alpha^t_ih_i

어텐션 값과 은닉상태 연결

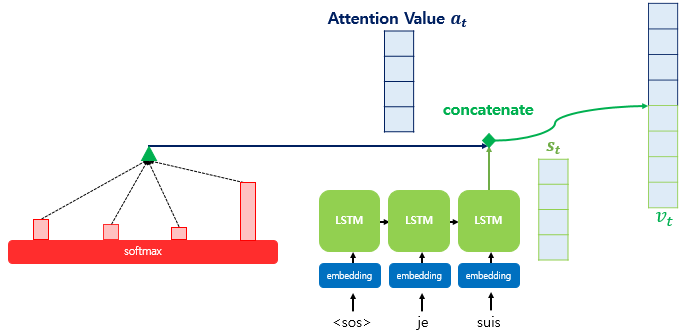
어텐션 함수의 최종값인 어텐션 값이 구해지면 어텐션 메커니즘은 현시점의 은닉 상태 $s_t$ 와 결합해 하나의 벡터로 만든다. 이를 $v_t$ 라고 하자.

이 $v_t$ 를 예측 연산의 입력으로 사용하여 예측 성능을 높이는것이 어텐션 메커니즘의 핵심이다.

논문에서는 $v_t$ 를 출력층으로 보내기 전에 신경망 연산을 한번 더 추가했다.

가중치 행렬과 곱하고 활성화 함수로 하이퍼볼릭탄젠트 함수를 통과시겨 새로운 벡터인 $\tilde s_t$ 를 구한다.

$W_c = 가중치 행렬$
$a_t = 어텐션 값$
$s_t = t시점의 은닉 상태$
$b_c = 편향$

\tilde s_t = tanh(W_c[a_t;s_t]+b_c)

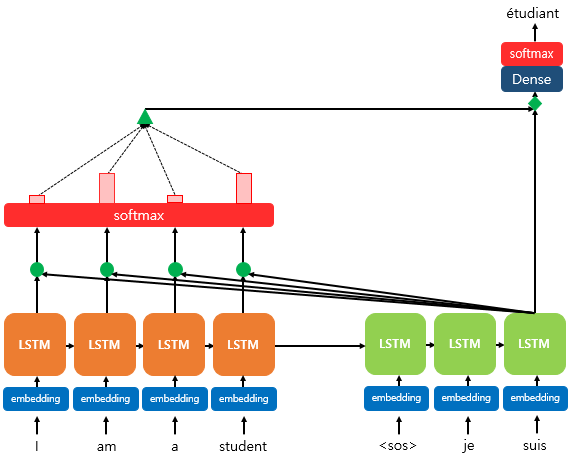
이 $\tilde s_t$ 는 출력층의 입력이 된다. 출력층에서도 소프트맥스 함수를 이용한다.

정리

어텐션 메커니즘은 seq2seq 모델의 한계를 극복하기 위해 등장한 기법으로, 디코더가 출력 단어를 예측할 때 인코더의 전체 입력 정보를 다시 참고하며 관련성이 높은 부분에 더 집중하는 방법이다.
위 과정을 통해 모델은 입력 문장의 특정 부분에 집중하여 더 정확한 출력을 생성할 수 있다!