[BOJ]14956 철학자의 산책

• Barkkkkking Dog 인증 최고난도 재귀 문제
• 이런 문제는 간단히 로직을 생각해보고 답을 보자
• 이런 모양을 Hilbert Curve라고 한다.
  • http://datagenetics.com/blog/march22013/index.html
    
    
• 문제
  • 영문 문제로 번역되지 않아 문제를 해석하는 것도 힘들 것이다.
  • 문제를 요약 정리하자면 n * n 크기의 미로에서 m걸을 가다 길을 잃었는대, 현재 좌표를 알아내는 문제
• 나의 생각
  • 정사각형을 4등분하고, 왼쪽 위부터 1, 2, 3, 4분면으로 나뉘었을 때,
    • 1사분면(우상단), 2사분면(좌상단)은 이전 단계의 산책 경로를
    • 3사분면(좌하단)은 이전 단계의 산책 경로를 오른쪽으로 90도 돌린 모양
    • 4사분면(우하단)은 이전 단계의 산책 경로를 왼쪽으로 90도 돌린 모양이다.
  • M의 특징의 맞는 해석
    1, 2사분면 해석 순서
    12
    03
    3사분면 해석 순서
    01
    32
    4사분면 해석 순서
    10
    23
  • 이를 활용해 재귀로 풀면 될듯
• 나의 팁
  • 모든 재귀는 f(n)과 f(n-1)의 변화를 보고 분해하면 풀이 가능
  • 특히, f(0)과 f(1)의 변화 또는, base condition을 제외한 f(1)과 f(2)의 변화를 분해하면 해결 가능하다.

• 풀이

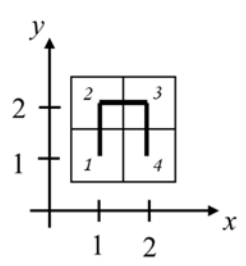
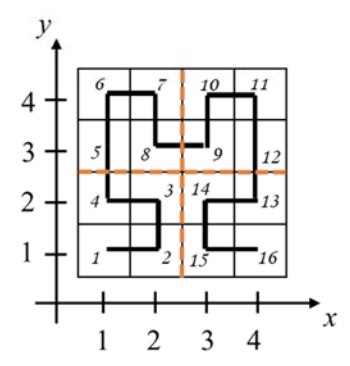
#include <bits/stdc++.h>
using namespace std;
pair<int , int> hilbert(int N, int M){
    //배열 좌표계가 아닌 일반 좌표계 사용(y축 대칭)
    pair<int, int> p;//x, y
    //base condition : W1
    if(N == 2){
        switch(M){
            case 0: //3사분면(좌하단)
                p = {1,1};
                return p;
            case 1: //2사분면(좌상단)
                p = {1,2};
                return p;
            case 2: //1사분면(우상단)
                p = {2,2};
                return p;
            case 3: //4사분면(우하단)
                p = {2,1};
                return p;
        }        
    }
    int half = N/2;
    int quadrant = M / (half*half);
    switch(quadrant){
        //3사분면(좌하단)
        case 0:
            p = hilbert(half, M % (half * half));
            //W2 -> W1을 보면 y = x 대각선 기준으로 대칭되어 두 좌표를 swap
            swap(p.first, p.second);
            return p;
        //2사분면(좌상단)
        case 1:
            p = hilbert(half, M % (half * half));
            //3사분면을 지나 y좌표가 half 만큼 상승
            p.second += half;
            return p;
        //1사분면(우상단)
        case 2:
            p = hilbert(half, M % (half * half));
            //3사분면, 2사분면을 지나 x좌표, y좌표가 half 만큼 상승
            p.first += half;
            p.second += half;
            return p;
        //4사분면(우하단)
        case 3:
            p = hilbert(half, M % (half * half));
            //W2 -> W1을 보면 y = -x 대각선 기준으로 대칭된다.
            //x좌표는 증가한다 이 두가지를 동시에 반영
            pair<int, int> temp = {2 * half - p.second + 1, half - p.first + 1};
            return temp;
    }
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    int N, M;
    cin >> N >> M;
    pair<int, int> result = hilbert(N, M-1);
    cout << result.first << ' ' << result.second << '\n';
    return 0;
}