코딩테스트
1.[BOJ]1406 에디터

sol1: stack 2개를 이용한 포인터 처리포인터의 왼쪽과 오른쪽에 위치하는 문자를 저장하는 두 스택(stack list & right)을 이용해 풀이L, D, B, P에 대한 처리스택 left의 모든 원소를 스택 right로 이동right의 모든 원소 출력 so
2.[BOJ]5397 키로거

sol1: stack left & right를 활용한 커서 문제 풀이sol2: list를 활용한 커서 문제 풀이
3.[BOJ]1158 요세푸스

sol1: queue를 활용해 원형 큐를 제작한 풀이sol2: list를 queue처럼 활용해 원형 큐를 제작한 풀이(뭐.. deque도 되고, 다 된다.)
4.[BOJ]1874 스택 수열

sol1: stack과 vector를 활용한 풀이현재 입력된 수와 cnt를 비교해가며 문제를 풀이
5.[BOJ]2493 탑

sol1: deque(stack + queue) 풀이스택에 임시 값을 넣는다.현재 높이보다 더 큰 값을 스택에서 발견할 때까지 pop()을 수행한다.수행 후, 스택의 top()엔 레이저 신호를 수신할 수 있는 pair 값이 남아있을 것해당 pair에서 원하는 값을 출력
6.[BOJ]6198 옥상 정원 꾸미기

sol1: stack을 활용한 풀이흔히 있는 스택문제의 유형(처음 보면 어렵지만 많이 보면 익숙해짐)for문을 돌며 현재 입력 값(height)과 stack의 top()의 값을 비교현재 입력 값(height)이 stack의 top()보다 크거나 같다면 stk.pop()
7.[BOJ]17298 오큰수

오른쪽이 큰 수를 찾는 문제값을 저장하고 오른쪽부터 처리해준다.스택의 top()이 현재 다루는 값보다 클 때까지 stk.pop()을 수행한다.stk.empty()라면 해당 위치에 -1을, 아니라면 stk.top()값을 넣어주고, 현재 값을 스택에 넣는다.최종적으로 an
8.[BOJ]6549 히스토그램에서 가장 큰 직사각형

풀지 못한 문제이다. 코딩테스트에서 나올 수 있는 최고난이도 수준의 스택 문제sol1: 이전 블록의 높이보다 작거나 같은 높이의 블록을 만날 때마다, 최대 넓이 계산마지막에 스택에 남은 블록에 대해 넓이 계산계산한 넓이 중 최 대값만을 기억해 출력
9.[BOJ]3015 오아시스 재결합

플레티넘V 등급 문제: 내 실력은 아직 부족하기 때문에, 풀이시간이 오래 걸릴 수 밖에 없음게다가 정답률도 20% -> 플레티넘V 이상의 문제라는 의미스택 + 문제에 맞는 풀이 필요long long으로 자료형 설정이 개같은거 때문에 시간낭비를 오지게 했다.
10.[BOJ]11003 최솟값 찾기

플레티넘 문제이기 때문에 풀지 못함(다만, 로직은 비슷하게 구성)스택 상위 난이도 문제 유형에서 deque로 업그레이드(고난이도)sol1: deque를 활용한 풀이stack 상위 버전의 문제에서 복잡해진 방식(top() => front() & back())으로 풀이 가
11.[BOJ]10799 쇠막대기

stk.top()이 아닌 stri-1(=이전 입력 값)을 활용하는 문제stk을 다룰 때, stk.top()만 사용한다는 고정관념에서 벗어나서 유연한 사고를 하자.
12.[BOJ]2178 미로탐색

카테고리를 DFS로 헷갈려서 풀다 -> 백트래킹 조지다 BFS인 것을 알고 푼 문제오답코드(DFS + 백트래킹): stack DFS로 구현 -> 재귀 DFS -> 재귀 백트래킹 순으로 구현sol1: BFS: 너비우선탐색: queue를 활용해 구현
13.[BOJ]7576 토마토

풀이 방식을 고안해내느라 풀이 시간이 오래 걸렸다.시작 지점(boardi == 1)을 미리 queue에 넣어놓고, bfs를 수행mysol: bfs를 이용한 풀이
14.[BOJ]4179 불!

mysol오답: 지훈이 이동 -> 불 이동정석 sol: 불 bfs 수행 -> 지훈이 수행 => 탈출 못할 시, IMPOSSIBLE bfs 2번 = 두 개의 큐 사용
15.[BOJ]10026 적록색약

정상인 / 적록색약인에 대해 구분지을 수 있는 RGB 영역의 개수를 각자 구하는 문제DFS / BFS 모두 해결 가능 sol1: BFS: queue를 사용해 구현좀 더 간단히 or 효율적으로 구현할 수 있는듯 싶다.\* sol2: DFS
16.[BOJ]7569 토마토

sol1: 3차원 BFS 풀이문제 자체는 일반 BFS와 크게 다르지 않으나 3차원 코드 경험치에 따라 구현 난이도가 달라진다.
17.[BOJ]7562 나이트의 이동

sol1: 일반적인 BFS를 활용한 풀이
18.[BOJ]5427 불

4179 불! 문제와 동일한 문제불과 플레이어의 BFS를 수행\-불 -> 플레이어 순서로 수행\-두 개의 queue, board, visited 배열 필요\-플레이어 BFS에서 경계 = 도착
19.[BOJ]2583 영역구하기

sol1: BFS sol2: DFS
20.[BOJ]2667 단지번호붙이기

sol1: DFSsol2: BFS
21.[BOJ]5014 스타트링크

sol1: BFS 풀이
22.[BOJ]6593 상범 빌딩

sol1: 3차원 BFS = 6방향 BFS 탐색
23.[BOJ]2206 벽부수고 이동하기

N회의 벽통과 허용 시 : visited 배열을 3차원으로 놓고 사용해당 문제는 1회 벽통과만 허용했지만, 본 코드는 N회의 벽 통과도 가능
24.[BOJ]9466 텀 프로젝트

sol1(시간초과): O(n^2) 코드로 시간초과가 난다. O(n) 풀이가 있다고 하는데, 내 뇌로는 O(n)은 생각나지 않아 풀이를 봤음 sol2: 정석 풀이법
25.[BOJ]2573 빙산

sol1: BFS 풀이 = 코드의 파트를 나누고, 파트별로 구현하는 것이 중요모두 녹을 때까지 반복1-1. BFS를 통해 빙산 개수 카운트(빙산의 개수가 2개 이상이면 정답 도출)1-2. 년도 증가1-3. 빙하 melting 수행: 물과 맞닿은 부분에 대해 적용1-4.
26.[BOJ]2146 다리 만들기

sol1: BFS 풀이\-접근법은 의외로 간단하다.\-각 대륙의 모든 점의 위치를 vector에 저장한 후, 대륙별로 각 대륙의 모든 점의 거리를 비교한다.\-거리의 최소값이 해답.
27.[BOJ]13549 숨바꼭질3

문제의 해석이 조금 어려웠다.sol1: deque를 활용한 BFSvisited 배열이 아닌 dist 배열을 통해 거리(cnt)를 저장하는 방식으로 풀이distk = anssol2: BFS 풀이(mysol)2배 이동 로직의 위치가 중요
28.[BOJ]1600 말이 되고픈 원숭이

sol1: BFS 풀이(횟수에 제한이 있는 BFS 유형)종종 보이는 불! 유형의 횟수에 제한이 있는 BFS이다.이런경우 visited 배열에 1차원을 더해 따로 방문체크를 해주면 된다.
29.[BOJ]13913 숨바꼭질 4

sol1(시간초과): BFS전체 경로를 저장해 시간초과매우 비효율적인 코드구성sol2: 직전정점 기억 BFS중요 포인트1: 직전에 방문한 x의 위치를 visited 배열에 저장한다.중요 포인트2: visited 배열에서 최초의 방문지점을 0으로 설정하면 안된다.poin
30.[BOJ]14442 벽 부수고 이동하기2

sol1: BFS를 활용한 풀이불! 시리즈 / 벽 부수고 이동하기 시리즈 등, 제한을 두는 BFS 풀이visited 배열에 차원을 더해 방문 처리
31.[BOJ]16933 벽 부수고 이동하기3

sol1(시간초과): BFS 코드 시간초과가 발생했고, 이를 해결하지 못한 코드이다. sol2: 답안 풀이 BFS
32.[BOJ]16920 확장 게임

sol: BFS 풀이플레이어 별로 queue를 따로 두고, BFS를 각 플레이어 오름차순대로 돌린다.해당 플레이어의 십자 전진 수(s_len)을 기준으로 반복하며, X칸 십자 이동을 구현한다.
33.[BOJ]11967 불켜기

sol: 역 BFS: 현재 방문 지점에서 큐에 넣고, 푸시하는 과정 필요adj 배열에 특정 방에서 킬 수 있는 방의 좌표(x2, y2)들을 저장한다.시작지점에 대한 처리를 수행한다.2-1. 방불 켜기2-2. 방문 처리2-3. 큐에 넣기역 BFS 를 수행한다.3-1. 현
34.[BOJ]17071 숨바꼭질5

숨바꼭질 시리즈 최종본(hhhard) sol(시간초과)
35.[BOJ]9328 열쇠

11967 불켜기 문제의 상위 호완 문제불켜기 문제를 해결한 입장에서 99% 풀이를 수행1% 오점: 열쇠를 주웠을 때, 잠금을 해재하는 방의 범위는 가장자리에서 침입 가능한 점을 기억해둬야 함sol: 잠금 해제 BFS
36.[BOJ]3197 백조의 호수

sol1: 매번 O(RC)에 걸처 빙판을 녹임 -> 두 백조가 있는 곳이 연결되었는지 BFS 탐색해당 방식 시간 초과sol2r, c: 호수 가로, 세로 길이 저장dx, dy: 네 방향 이동을 위한 배열waterQ: 빙하 제거를 위한 물의 좌표를 저장swanQ: 백조가
37.[BOJ]20304 비밀번호 제작

sol: BFS 풀이Make_max_bit_size()를 통해 최대 비트 수(max_bit_size)를 구한다.넣어둔 로그인 시도 암호를 기반으로 BFS 수행XOR을 수행하는 이유: 가장 거리가 먼 비밀번호를 생성하기 위함
38.[BOJ]18511 큰 수 구성하기

재귀 문제 풀이 4단계1단계: 굳이성: 문제 풀이를 위함이라 굳이 써야 함2단계: BaseCondition: a > N 이상의 수가 되면 종료3단계: 분해: 수가 정방향으로 증가하도록 $$dfs(a + veci n, n 10)$$ 설계4단계: 조합: max 값을
39.[BOJ]10994 별찍기-19

별찍기 재귀 sol: 피라미를 위에서 본 방향별찍기1별찍기2별찍기3별찍기 재귀는 대대손손 board를 만드는 방식으로 풀이한다.점화식을 기반으로 N번째 직사각형 위치의 값을 할당한다.
40.[BOJ]4779 칸토어 집합

재귀 sol$$base condition$$을 정의한다.(문제에서 case 0이 주어져서 설정하기 쉬움)$$f(base condition) -> f(base condition+1)$$의 관계에서 $$f(n) -> f(n+1)$$의 점화식을 발견한다.점화식에 따른 함수를
41.[BOJ]24460 특별상이라도 받고 싶어

재귀 문제가 풀리기 시작했다.Base Condition 정의$$f(Base Condition) -> f(Base Condition + 1)$$으로 가는 규칙 발견위 코드를 활용한 문제 해결sol1\-n = 1칸이 될 경우 그 칸을 반환\-사각형을 4분면으로 나눠 재귀
42.[BOJ]28075 스파이

sol1. DFS식 재귀: 장소에 따른 차감 적용과 재귀를 통한 구현
43.[BOJ]2630 색종이 만들기

* sol1: 재귀* 현재 넓이 색종이에 대한 테스트 네방향 갈라지기
44.[BOJ]1780 종이의 개수

sol DSF 재귀: 사각형을 등분해는 풀이사각형을 9등분내고, 각 사각형을 탐색하는 풀이법
45.[BOJ]17829 222-풀링

sol 재귀: 사각형은 $$2^n$$의 한 변의 길이로 주어진다.절반씩 파고들고, 한 변의 길이가 2가 되었을 때, 부턴째 2번째로 큰 값을 가져온다.사각형을 4등분해 가져온 각 값 중, 두번째로 큰 값을 리턴한다.
46.[BOJ]10997 별찍기 - 22

sol: 재귀: 해결하지 못했고, 제일 싫어하는 별찍기 재귀 문제 재귀 사진가로 길이 = 1 -> 5 -> 9 -> 13 = 4(N-1)+1 = 4N - 3세로 길이 = 1 -> 7 -> 11 -> 15 = 가로 길이 + 2(N != 1)각 시작점에서 아래 과정으로 별
47.[BOJ]18222 투에-모스 문자열

투에-모스 문자열이라는 유명한 재귀 유형점화식이 존재한다. = 점화식을 기반으로 재귀 함수를 구형하면 된다.$$T(0) = 0$$$$T(2n) = T(n)$$$$T(2n+1) = 1 - T(n)$$sol1: ???어떤 미친 사람이 5줄로 해결 가능하다고 작성한 코드(보
48.[BOJ]16505 별

재귀는 풀리다가도 안풀리고, 안풀리다가도 풀리는 것이 문제는 안풀리다 풀렸다. 기모띠board의 길이는 가로 / 세로 : $$2^N$$임을 파악이 문제를 푼 열쇠는 $$f(k) = 3 \* f(k-1)$$임을 알아차린 것이다.(단 각 삼각형의 위치는 조정)각 줄 끝에
49.[BOJ]23304 아카라카

sol: 재귀 풀이법문제의 Base Condition을 이용한다 : $$str.size() == 1$$현재 문자열이 팰린드롬임을 확인한다.문자열을 두 갈래로 재귀 실행한다. $$substr(), ceil()사용$$ //ceil()은 홀수, 짝수 구분 없이 구현하기 위함
50.[BOJ]1991 트리순회

51.[BOJ]1992 쿼드트리

sol1: 재귀 풀이4갈래로 나뉘어 탐색범위 탐색 수행 중, 시작점의 값과 다른 값이 발견되면, 탐색 종료
52.[BOJ]1074 Z

sol 재귀Z모양으로, board의 칸을 방문했을 때, r행 c열의 방문 순서를 출력하는 것시간초과 => 4사분면 모두 탐색하는 방식이 아닌 한 분면만 탐색하는 방식 적용
53.[BOJ]1914 하노이 탑

$$하노이탑 문제[재귀]$$ 재귀로 유명한 하노이탑 문제다. 1번 영역 / 2번 영역 / 3번 영역 1번 영역에 쌓인 N층의 탑을 3번 영역으로 옮기는 문제 base condition N = 1 -> 1번 영역의 쌓인 1층 탑을 3번 영역으로 이동$$(move)$$시
54.[BOJ]9934 완전 이진 트리

sol: 재귀k층 2차원 배열에 각 층의 원소를 넣고, 출력시작 지점 / 중간 지점 / 끝 지점 기점으로 분리하게 처리
55.[BOJ]1662 압축

sol1(메모리초과): 재귀 카테고리 문제를 재귀를 사용하지 않고 해결하니 메모리 초과 발생sol2(재귀)입력받은 압축된 문자열의 왼쪽부터 탐색재귀 함수 인덱스를 0 - end까지 탐색현재 문자가 숫자라면 -> cnt(길이)를 증가시키고 방문 체크현재 문자가 '('라면
56.[BOJ]5904 Moo 게임

sol1(메모리 초과): 재귀문자열의 상상 이상으로 길어져서 메모리 초과가 발생할 것을 예상했다.sol2: 재귀문자열 점화식$$S0 = "moo"$$$$Sk = Sk-1 + "m" + "o" \* (k + 2) + Sk-1$$문자열 길이 점화식: $$len(Sk) =
57.[BOJ]20164 홀수 홀릭 호석

sol: 재귀odd_num 함수를 통해 문자열로 된 숫자의 홀수의 개수를 카운트한자리수: max_ans/min_ans 갱신두자리수: 각 자리수를 더해 새 문자를 만들고, 이를 기반으로 recursio 수행세자리수: 각 문자의 길이를 결정짓는 이중 for문을 돌려 세 문
58.[BOJ]2448 별 찍기 - 11

sol: 별찍는 문제재귀의 가장 기본이자 쉽지 않은 유형base condition : N = 3밑변의 길이 = 2 \* N - 1임을 파악삼각형의 높이 = N임을 파악이를 토대로 재귀 함수 구성
59.[BOJ]10993 별 찍기 - 18

sol1: 재귀복잡한 도형을 출력하는 재귀 문제재귀가 두 단계(짝수 = ▼ / 홀수 = ▲)로 나뉘어 진행출력도 마찬가지로 두 단계(짝수 = ▼ / 홀수 = ▲)로 나뉘어 진행base condition = 시작점에 \* 출력도형의 너비 = $$pow(2, N+1) -
60.[BOJ]16719 ZOAC

sol: 재귀알고리즘사전상 가장 앞선 단어 추출추출한 문자열 기준 오른쪽 문자열 이동 & 탐색추출한 문자열 기준 왼쪽 문자열 이동 & 탐색TIP 추출한 문자의 원래 문자열상 위치에 삽입하는 방법char 배열에 해당 문자의 위치를 계산한 후, 해당 배열을 모두 돌며 '
61.[BOJ]1030 프렉탈 평면

sol풀 엄두도 내지 못했다. 그러므로 분석한다.재귀 카테고리에 있지만 재귀를 안쓴 풀이가 가장 깔끔해서 가져왔다.
62.[BOJ]9997 폰트

sol : 재귀bit를 이용해 현재 문자열 표시재귀를 이용해 모든 경우의 수 조합재귀현재 문자를 포함시킨 경우현재 문자를 포함시키지 않는 경우b == (1<<26)-1 27비트(10...0) - 1 = 26비트(1...1) 즉, 모든 알바벳이 존재하는 경우를
63.[BOJ]14956 철학자의 산책
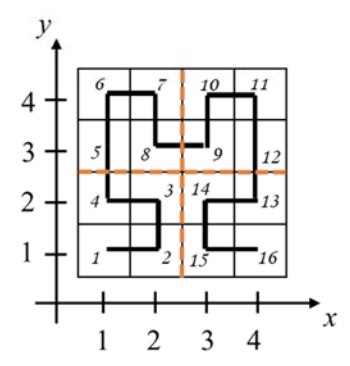
재귀 Barkkkkking Dog 인증 최고난도 문제 이런 문제는 간단히 로직을 생각해보고 답을 보자 나의 생각 정사각형을 4등분하고, 왼쪽 위부터 1, 2, 3, 4분면으로 나뉘었을 때, 1, 2사분면은 이전 단계의 산책 경로를 3사분면은 이전 단계
64.[BOJ]15649 N과 M (1) - 순열

sol : 백트래킹 재귀 DFS순열 $$nPm$$의 코드식 구현앞에 나온 수 < 뒤의 나온 수이미 등록된 수 중복 불가 = visited를 통해 체크고찰visited가 없다면 1...1 to N...N의 수를 순환하는 수열visited를 통해 방문된 수를 선점수가
65.[BOJ]15650 N과 M (2) - 조합

sol : 백트래킹 재귀 DFS순열 $$nPm$$의 코드식 구현앞에 나온 수 < 뒤의 나온 수이전 단계의 수를 의미하는 인자 하나(num)를 추가해 이전 단계의 수 이상의 수만 받아들이도록 사용고찰visited가 없다면 1...1 to N...N의 수를 순환하는
66.[BOJ]15651 N과 M (3) - 중복 순열

sol : 백트래킹 재귀 DFS$$nPm$$ 중복순열중복 허용visited 배열 필요 X대소 제한 없음추가 인자 필요 X
67.[BOJ]15652 N과 M (4) - 중복 조합

`
68.[BOJ]15654 N과 M (5)

1 to N이 아닌 Input으로 주어진 값을 순열로 출력sol : 재귀
69.[BOJ]15655 N과 M (6)

sol : 백트래킹 재귀 DFS조합(Combination) : $$nCm$$의 코드식 구현$nCr = n! / ((n - r)! \* r!)$앞에 나온 수 < 뒤의 나온 수이전 단계의 수를 의미하는 인자 하나(num)를 추가해 이전 단계의 수 이상의 수만 받아들이
70.[BOJ]15656 N과 M (7)

sol : 백트래킹 재귀 DFS중복순열 : $$n∏m$$의 코드식 구현$$n∏r = n^r$$중복 허용visited 배열 필요 X대소 제한 없음추가 인자 필요 X
71.[BOJ]15657 N과 M (8)

sol : 백트래킹 재귀 DFS중복조합 : $$nHm$$의 코드식 구현$$nHr = n+r-1Cr$$중복 허용visited 배열 필요 X대소 제한 있음추가 인자 필요 O
72.[BOJ]15663 N과 M (9)

sol1 : 백트래킹 재귀 DFS순열의 중복 저장 / 출력을 막는다.이를 위해 set에 저장 후 출력
73.[BOJ]15664 N과 M (10)

sol1 : 백트래킹 재귀 DFS순열의 중복 저장 / 중복된 순열의 출력을 막는다.이를 위해 중복을 제거하는 set에 저장 후 출력sol : more efficient순열의 앞부분은 중복되지 않음뒤에 나오는 순열의 중복만 막으면 더 효울적인 코드 구성 가능
74.[BOJ]15665 N과 M (11)

sol1 : 백트래킹 재귀 DFS순열의 중복 저장 / 중복된 순열의 출력을 막는다.이를 위해 중복을 제거하는 set에 저장 후 출력sol2 : more efficient순열의 앞부분은 중복되지 않음뒤에 나오는 순열의 중복만 막으면 더 효울적인 코드 구성 가능
75.[BOJ]15666 N과 M (12)

sol1 : 백트래킹 재귀 DFS순열의 중복 저장 / 중복된 순열의 출력을 막는다.이를 위해 중복을 제거하는 set에 저장 후 출력sol2 : more efficient순열의 앞부분은 중복되지 않음뒤에 나오는 순열의 중복만 막으면 더 효울적인 코드 구성 가능
76.[BOJ]1182 부분수열의 합

sol 백트래킹 DFSinput 배열의 정렬 X : 정렬을 하던 말던, 수열의 구성 방식이 맞다면, 모든 부분 수열의 부분합을 체크부분 수열에 포함된 원소는 다시 나올 수 없음중복 불가 & 알파벳 제한
77.[BOJ]1759 암호 만들기

흔하디 흔한 DFS + 백트래킹 문제걸리는 점은 자음 모음의 개수암호의 길이가 L이 될 때, 자음 모음의 개수가 조건을 충족하면 값 출력자음: 최소 1개모음: 최소 2개
78.[BOJ]9663 N-Queen

N-Queen아주 유명한 백트래킹 + 완전탐색 문제아래 조건을 만족하며 퀸을 N X N 보드에 배치해야한다.가로 배치 체크는 자동으로 수행세로 배치 체크대각선 배치 체크조건1: 퀸끼리는 가로상으로 만나면 안된다.조건2: 퀸끼리는 세로상으로 만나면 안된다.조건3: 퀸끼리
79.[BOJ]1941 소문난 칠공주

solarr : 학생들의 배열을 저장visited : 조합에 뽑힌 인원을 체크하는 배열checked : 조합에 뽑힌 학생들의 연결을 확인하기위한 배열25명 중 7명을 뽑는다.DFS()를 통해 조합 구현DFS()의 depth가 7이면 7명의 조합($25C7$)이 뽑힌것깊
80.[BOJ]16987 계란으로 계란치기

soleggs 배열에 N개 egg의 내구도와 무게를 저장한다.DFS(0) : 에그를 0부터 계란치기를 수행한다.cur_egg_idx == N으로 현재 단계가 N이 될 때까지 수행한다.N이 된 경우 is_broken 배열의 부서진 계란의 수를 체크해 ans에 최댓값을 대
81.[BOJ]10974 모든 순열

sol: 백트래킹
82.[BOJ]16922 로마 숫자 만들기

sol: 백트래킹DFS로 풀려했고, 일반적인 백트래킹으로 풀려했지만, 성능 상 시간 초과가 발생해 불필요한 케이스 가지치기
83.[BOJ]18429 근손실

sol: 근손실은 못참지.. 푼다.백트래킹으로 푼다.
84.[BOJ]2992 크면서 작은 수

sol: 백트래킹next_permuation을 통한 간단한 풀이 가능
85.[BOJ]21745 눈덩이 굴리기

sol: 백트래킹눈덩이를 굴리는 위치는 01 - N까지 눈덩이를 굴릴 수 있다.
86.[BOJ]5639 이진 검색

sol1(시간초과): S에 문자열을 추가해 T로 만드는 방식sol2: T에서 문자열을 삭제해 S로 만드는 방식앞/뒤에 A/B가 오는걸 토대로 불필요한 재귀호출을 생략 가능
87.[PGS]서울에 위치한 식당 목록 출력하기

JOIN + GROUP BY + ROUND
88.[PGS]재구매가 일어난 상품과 회원 리스트 구하기

GROUP BY다중 GROUP BY A, B는 A, B 모두 동일한 튜플에 의한 그룹화 수행
89.[PGS]오프라인/온라인 판매 데이터 통합하기

UNION여러 쿼리문들을 합쳐서 하나의 쿼리문으로 만들어주는 방법중복 값 제거중복된 값을 제거하는 연산이 추가로 수행되기 때문에 UNION ALL보다 속도가 느리다.UnionALL여러 쿼리문들을 합쳐서 하나의 쿼리문으로 만들어주는 방법이다.중복 값 포함사용 방법컬럼 명
90.[PGS]업그레이드 된 아이템 구하기

다중 조인다중 조인을 통해 과거 자료와 연속 연결
91.[PGS]가격이 제일 비싼 식품의 정보 출력하기

LIMIT 상위 N개 레코드where X = (select 절) : 단일 값을 출력한다면, 해당 방식으로 사용 가능
92.[PGS]중복 제거하기

DISTINCT + IS NOT NULL
93.[PGS]경기도에 위치한 식품창고 목록 출력하기

IF(조건, true, false) + LIKE
94.[PGS]업그레이드 할 수 없는 아이템 구하기

IN
95.[PGS]조회수가 가장 많은 중고거래 게시판의 첨부파일 조회하기

CONCAT : 문자열을 쉼표(,) 기준으로 연결
96.[PGS]조건에 부합하는 중고거래 상태 조회하기

CASE WHEN THEN END
97.[PGS]조건별로 분류하여 주문상태 출력하기

CASE WHEN THEN 2 ELSECASE 후, 바로 WHEN이 이어서 온다.특정 값의 범위를 지정한다.
98.[PGS]조건에 맞는 사용자 정보 조회하기

CONCAT(,) + SUBSTR(STR, 시작, 글자수)
99.[PGS]자동차 평균 대여 기간 구하기

ROUND+AVG +TIMESTAMPDIFFHaving은 변경된 속성을 접근 가능하다.
100.[PGS]오랜 기간 보호한 동물(2)

DATETIME DIFF + LIMIT
101.[PGS]연도 별 평균 미세먼지 농도 조회하기

'속성명'+ROUND+AVG
102.[PSG]자동차 대여 기록 별 대여 금액 구하기

WITH VALUE AS ( ... )테이블을 만들고, 후에 SELECT FROM VALUE를 통해 이용
103.[PGS]조건에 맞는 개발자 찾기

&, |, ^을 통한 직접적인 비트 연산이 가능JOIN을 사용하지 않아도, 여러 테이블의 정보를 활용하는 것이 가능
104.[PGS]주문량이 많은 아이스크림들 조회하기

WITH VALUE AS (...)+UNION를 활용한 풀이JOIN만을 활용한 풀이
105.[PGS]없어진 기록 찾기

NOT IN을 활용한 풀이LEFT JOIN을 활용한 풀이
106.[PGS]특정 기간동안 대여 가능한 자동차들의 대여비용 구하기

107.[PGS]그룹별 조건에 맞는 식당 목록 출력하기

108.FrontEnd 개발자 찾기

& + SUM: 개발자가 FrontEnt 스킬을 여러개 가진 경우 여러번 나오기 때문에 그에 대한 처리를 SUM을 통해 수행DISTINCT + &: 개발자가 FrontEnt 스킬을 여러개 가진 경우 여러번 나오기 때문에 그에 대한 처리를 SUM을 통해 수행
109.입양 시각 구하기(1)

GROUP BY + WHERE
110.[PGS]가격대 별 상품 개수 구하기

TIPS -> SELECT - WHERE까지 적용 후, GROUP BY가 적용됨SELECT에서 AS를 사용한 별칭을 WHERE에선 사용 불가SELECT에서 AS를 사용한 별칭을 GROUP BY에선 사용 불가
111.[코테]SQL의 모든것

코딩 테스트에서 사용되는 SQL 문법의 모든 것을 요약 기본형 행 함수(행 값 융합) 행 함수(행 값 수정) where or and in not between and exists like group by ... having 특정 (행)에 따라 그룹화 행 함수(