최장 증가 부분 수열 (LIS, Longest Increasing Subsequence)
원소가 n개인 배열의 일부 원소를 골라내서 만든 부분 수열 중, 각 원소가 이전 원소보다 크다는 조건을 만족하고(오름차순), 그 길이가 최대한 부분 수열을 최장 증가 부분 수열이라고 함
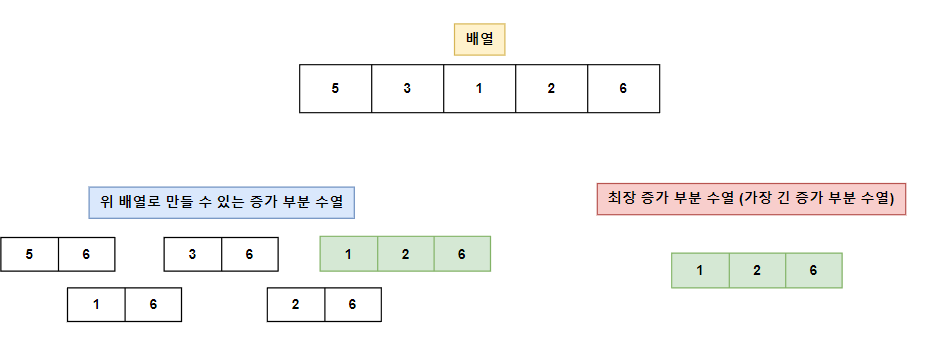
방법 1 : DP를 사용한 방법
사실 가장 단순한 방법은 완전 탐색이긴 한데, 이 경우는 너무 비효율적이라서 제외하고, DP를 사용하는 방법이 그나마 간단하면서 효율적인 방법이다.
수열의 한 원소 k에 대해, 그 원소에서 끝나는 최장 증가 수열을 만든다고 한다면 그 앞 원소들은 전부 k보다 작을 것이다. 따라서 앞 원소들에 대해 그 각각의 원소에서 끝나는 최장 증가 수열의 길이를 안다면, k에서 끝나는 최장 증가 수열의 길이도 알 수 있을 것이다.
이러한 점을 살려 DP에 적용해보면 DP[i] = "i번째 인덱스에서 끝나는 최장 증가 수열의 길이"로 정의될 수 있다!
그래서 dp[i]의 값은 i번째 원소와 이전 원소들을 비교하며 i번째 원소보다 작은 원소들 중 DP가 가장 큰 값에 1을 더한 값이다.
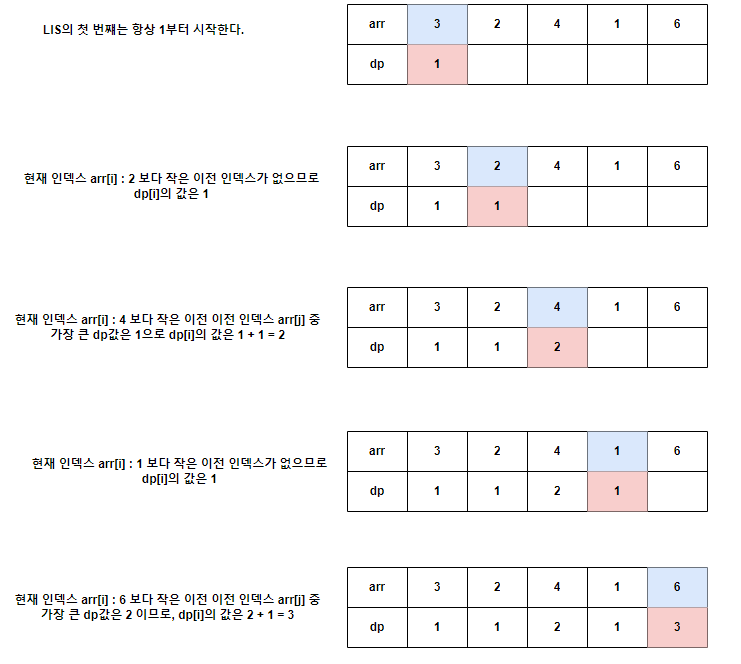
length = int(input());
arr = list(map(int, input().split()));
# 주어진 수열과 같은 크기의 dp 배열을 만들어주고 1로 전부 초기화 (나 하나는 무조건 들어간다고 생각하면 쉬움)
dp = [1 for i in range(length)];
# i를 길이만큼 돌면서
for i in range(length):
# i보다 작은 j까지 돌면서
for j in range(i):
# 만약 j가 i보다 작으면 현재 i번째 dp값이랑 j번째 dp 값에 1을 더한 값 중(j를 포함한 LIS에 i를 더 붙여줌) 더 큰 값을 dp[i]로 바꿔줌
if (arr[j] < arr[i]):
dp[i] = max(dp[i], dp[j] + 1);
# dp 배열에서 가장 큰 원소가 LIS 길이가 됨
print(max(dp));하지만 시간 복잡도가 O(n^2)라는 단점이 있다!
방법 2 : 이분 탐색을 사용한 방법
이분 탐색을 이용하여 최장 증가 부분 수열의 길이를 구할 수도 있는데 이 경우에는 시간 복잡도가 O(NlogN)으로 줄일 수 있다.
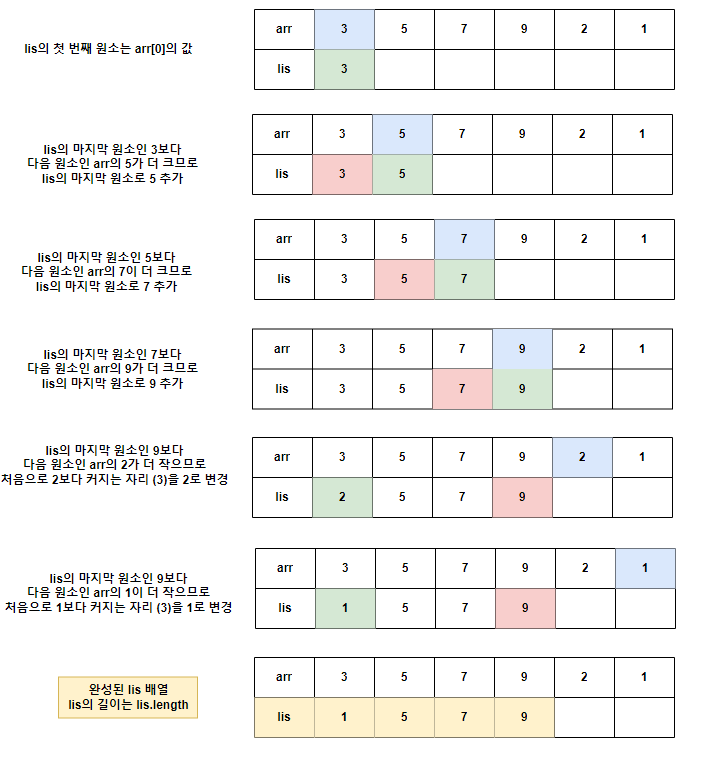
import bisect
length = int(input());
arr = list(map(int, input().split());
# 첫번째 원소로 dp를 초기화시켜줌
dp= [arr[0]];
for i in range(1, length):
# 현재 존재하는 dp의 맨 마지막 원소인 -1번째 값보다 현재 i번째 원소가 더 크다면 dp 맨 뒤에 추가해줌
if dp[-1] < arr[i]:
dp.append(arr[i]);
# 현재 존재하는 dp의 맨 마지막 원소인 -1번째 값보다 현재 i번째 원소가 작거나 같다면 기존 dp에서 현재 위치의 원소가 들어갈 자리를 찾아 해당 위치에 있는 원소 대신에 들어감
# 이건 가능한 한 작은 수로 시작하는 부분 수열을 만들기 위해서임!
else:
idx = bisect.bisect_left(dp, arr[i]);
dp[idx] = arr[i];
print(len(dp))참고
https://github.com/gyoogle/tech-interview-for-developer/blob/master/Algorithm/LIS%20(Longest%20Increasing%20Sequence).md
https://minit-devlog.tistory.com/57
https://hstory0208.tistory.com/entry/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-LIS%EC%B5%9C%EC%9E%A5-%EC%A6%9D%EA%B0%80-%EB%B6%80%EB%B6%84-%EC%88%98%EC%97%B4%EC%9D%B4%EB%9E%80
