LCA(최소 공통 조상) 알고리즘

LCA

LCA란 트리에서 두 정점 u, v에서 가장 가까운 공통조상을 찾는 과정을 말함. 두 점 사이의 거리를 구할 때 사용하며 두 노드에서 시작하여 올라가면서 부모 노드가 같아질 때까지 찾아가면 됨.

• A와 B 두 점 사이의 거리 = 1부터 A까지의 거리 + 1부터 B까지의 거리 - 1부터 LCA까지의 거리 * 2

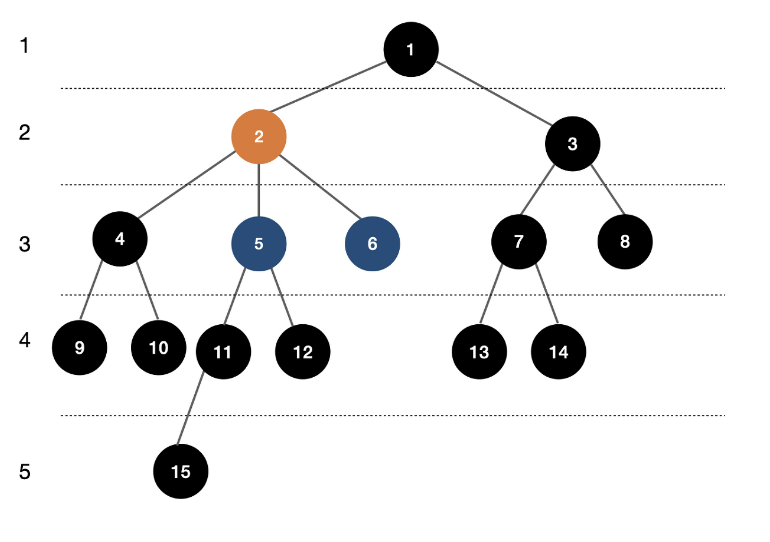
이 그림에서 5번과 6번 노드의 최소 공통 조상, LCA는 2번 노드임.
5번과 6번 노드의 거리는 1부터 5까지의 거리(2) + 1부터 6까지의 거리(2) - 1부터 2까지의 거리 2(1 2) 해서 2가 됨.

일반적인 LCA 풀이 로직

1. 1번 루트노드를 기준으로 DFS 탐색을 하면서 각 노드의 트리의 높이(h)와 부모 노드(parent)를 저장해줌
2. LCA를 구하기 위한 a, b번 노드가 주어지면 해당 두 노드의 h를 일정하게 맞춤(a 높이 == b 높이)
3. 높이가 맞추어졌으면 각 부모 노드가 일치할 때까지 비교하여 구함 (최대 LCA는 루트 노드 1)

이 방법같은 경우 O(NM)이라는 시간 복잡도를 가짐

일반적인 LCA 코드 - 파이썬

import sys
sys.setrecursionlimit(10**5)

# 루트노드부터 시작하여 깊이를 구하는 함수
def dfs(now, depth):
    c[now] = True # 현재 노드 방문 처리
    d[now] = depth # 현재 노드 깊이 저장

    for next_ in graph[now]:
    	# 깊이를 이미 구한 경우 무시
        if c[next_]:
            continue
        # next_의 부모를 현재 노드로 설정
        parent[next_] = now
        # 다음 노드 재귀 진행
        dfs(next_, depth + 1)


def lca(a, b):
    # 두 노드의 깊이가 다를 경우
    while d[a] != d[b]:
    	# 깊이가 큰 노드가 부모 노드로 이동
        if d[a] > d[b]:
            a = parent[a]
        else:
            b = parent[b]
    # 깊이는 같지만 두 노드가 서로 다를 경우
    while a != b:
    	# 두 노드를 한 번에 부모 노드로 이동
        a = parent[a]
        b = parent[b]
    return a


n = int(input())
arr = []
maxN = 0
# 간선 정보
for _ in range(n-1):
    x, y = map(int, input().split())
    arr.append([x, y])
    maxN = max(maxN, max([x, y]))

# 그래프 생성
graph = [[] for _ in range(maxN+1)]
for x, y in arr:
    graph[x].append(y)
    graph[y].append(x)

# 부모 노드 정보 저장 배열
parent = [0] * (maxN + 1)
# 노드의 깊이 저장 배열
d = [0] * (maxN + 1)
# 방문 처리 배열
c = [0] * (maxN + 1)

dfs(1, 0) # 루트노드 1 깊이는 0
m = int(input())
for _ in range(m):
    x, y = map(int, input().split())
    print(lca(x, y))

DP를 활용한 LCA 코드 - 파이썬

일반적인 LCA 코드는 시간 복잡도가 굉장히 좋지 않기 떄문에 DP를 활용하여 효율적인 방식으로 만들 수 있다!

import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**5) # 재귀 깊이 설정 
LOG = 21 # 2^20 = 1,000,000

n = int(input())
# 부모 노드 정보 저장 배열
# parent[j][i]는 노드 j의 2^i번째 조상을 의미함
parent = [[0]*LOG for _ in range(n+1)] 
# 노드의 깊이 저장 배열
d = [0] * (n+1) 
# 방문 처리 배열
c = [0] * (n+1) 
# 연결 정보 저장 배열
graph = [[] for _ in range(n+1)]

for _ in range(n-1):
    a, b = map(int, input().split())
    graph[a].append(b)
    graph[b].append(a)

# 루트노드부터 시작하여 깊이를 구하는 함수
def dfs(x, depth):
    c[x] = True # 현재 노드 방문 처리
    d[x] = depth # 현재 노드 깊이 저장

    for y in graph[x]:
        if c[y]:
            continue
        # y의 직계 부모를 x로 설정
        parent[y][0] = x
        dfs(y, depth + 1)

# 전체 부모 관계를 설정하기
def set_parent():
    dfs(1, 0) # 루트노드 1번부터 시작 
    for i in range(1, LOG): #2^i번째 조상을 설정
        for j in range(1, n+1):
            # j의 2^i번째 조상은 j의 2^(i - 1)번째 조상의 2^(i - 1)번째 조상
            parent[j][i] = parent[parent[j][i-1]][i-1]

# A와 B의 최소 공통 조상 찾기 
def lca(a, b):
    # B가 더 깊도록 설정 
    if d[a] > d[b]:
        a, b = b, a
    # 깊이가 동일하도록 해줌
    # 깊이가 다르면 b를 위로 올려줌
    for i in range(LOG - 1, -1, -1):
        if d[b] - d[a] >= (1 << i):
            b = parent[b][i]
            
    # 부모가 같아졌으면(공통 조상을 찾았으면)
    if a == b:
        return a

	# 위에서부터 내려오면서 LCA를 찾는데 i는 1씩 줄어드는 형태로 반복됨.
    # a에서 i^2만큼 떨어져있는 부모와 b에서 i^2만큼 떨어져 있는 부모가 같은지를 비교함
    # 만약 같다면 공통 조상인건 맞는데 더 가까운 공통 조상이 있을 수 있으니까 i값을 내려서 더 탐색함
    # 만약 다르다면 노드를 크게 건너뛰기 때문에 LCA를 지나쳤을 가능성이 있어서 a와 b를 지금 탐색 노드로 옮겨줌
    for i in range(LOG-1, -1, -1):
    	# 조상을 향해 거슬러 올라가기 
        if parent[a][i] != parent[b][i]:
            a = parent[a][i]
            b = parent[b][i]
    # 부모가 찾고자 하는 조상 반환
    return parent[a][0]


set_parent()
m = int(input())

for i in range(m):
    a, b = map(int, input().split())
    print(lca(a, b))

참고

https://github.com/gyoogle/tech-interview-for-developer/blob/master/Algorithm/LCA(Lowest%20Common%20Ancestor).md
https://dogsavestheworld.tistory.com/entry/python-%EB%B0%B1%EC%A4%80-1761%EB%B2%88-%EC%A0%95%EC%A0%90%EB%93%A4%EC%9D%98-%EA%B1%B0%EB%A6%AC
https://loosie.tistory.com/364
https://yiyj1030.tistory.com/517