BFS, DFS
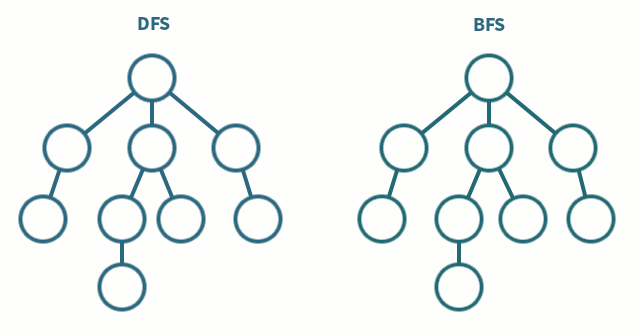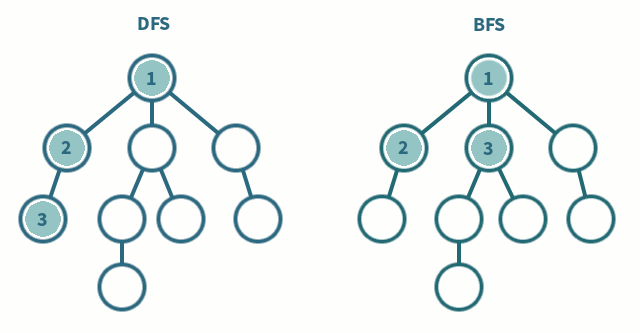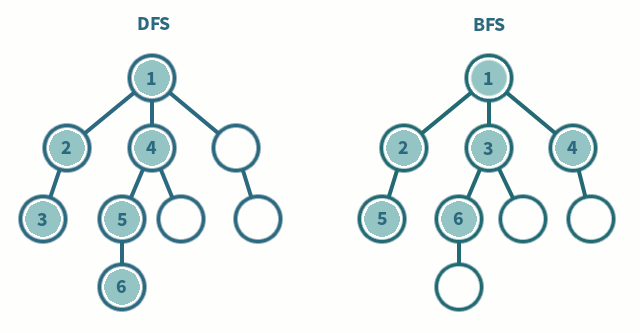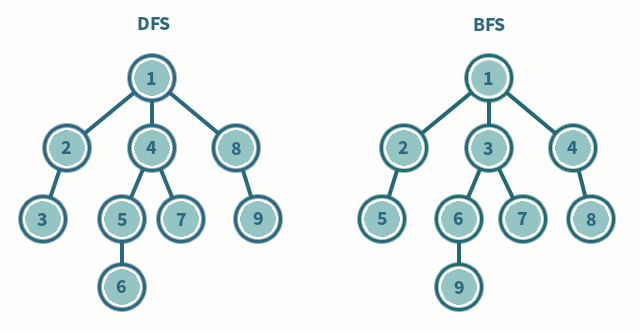
BFS는 현재 정점에 연결된 가까운 점들부터 탐색하는 방식으로 큐를 이용해서 구현합니다. 방문한 노드를 큐에 저장하고 먼저 저장된 노드부터 출력합니다. 최단거리를 구해야하거나 검색 대상의 규모가 크지 않고 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않은 경우 사용합니다.
from collections import deque
def bfs(graph, start):
visited = set()
queue = deque([start])
while queue:
vertex = queue.popleft()
if vertex not in visited:
print(vertex, end=' ')
visited.add(vertex)
queue.extend(graph[vertex])DFS는 현재 정점에서 갈 수 있는 점들까지 들어가면서 탐색하는 방식으로 스택 또는 재귀함수로 구현합니다. 방문한 노드를 스택에 저장하고 더 이상 탐색할 수 없을 때 스택에서 노드를 꺼내어 역순으로 출력합니다. 검색 대상 그래프가 크거나 경로마다의 특징을 저장해두어야 할 경우 사용합니다.
def dfs(graph, start, visited=None):
if visited is None:
visited = set()
visited.add(start)
print(start, end=' ')
for neighbor in graph[start]:
if neighbor not in visited:
dfs(graph, neighbor, visited)
최장 증가 부분 수열(LIS)
최장 증가 부분 수열이란 원소가 n개인 배열의 일부 원소를 골라내서 만든 부분 수열 중 각 원소가 이전 원소보다 크다는 조건을 만족하고, 그 길이가 최대한 부분 수열을 최장 증가 부분 수열이라고 합니다.
최장 증가 부분 수열 구현 방법
- DP 사용
각 i위치에서 끝나는 LIS의 최대 길이를 저장하는 리스트를 통해 LIS 길이를 구함. 시간 복잡도는 O(N^2).
dp[i] = "i번쨰 인덱스에서 끝나는 최장 증가 수열의 길이"로 정의함.
- DP 사용
def lis_dp(arr):
n = len(arr)
dp = [1] * n # 각 원소는 최소 자기 자신 하나로 LIS 가능
for i in range(n):
for j in range(i):
if arr[j] < arr[i]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp)- 이분 탐색 사용
이분 탐색으로 수열을 유지하며 가능한 가장 작은 값으로 교체해 LIS 길이를 구함. 시간 복잡도는 O(N log N).
기존 수열의 각 원소가 LIS에 들어갈 위치를 찾는 원리로 동작하며 혈ㄴ재 원소를 배열에 넣어 LIS를 유지하려고 할 떄, 최적의 위치를 찾아가는 방식임.
- 이분 탐색 사용
import bisect
def lis_binary(arr):
tail = []
for num in arr:
idx = bisect.bisect_left(tail, num)
if idx == len(tail):
tail.append(num) # 새로운 LIS 확장
else:
tail[idx] = num # 더 작은 값으로 교체
return len(tail)최소 공통 조상 (Lowest Common Ancestor, LCA)
두 노드의 가장 가까운 공통 조상을 찾는 알고리즘입니다. 트리 구조에서 두 노드 간의 관계를 빠르게 파악할 수 있어 트리 구조의 질의 처리에 자주 사용됩니다. 이때, 조상이란 루트에서부터 내려오는 경로 상에 있는 노드를 말합니다.
기본적으로 미리 각 노드의 부모, 깊이 정보를 저장해두고 두 노드의 깊이를 맞춘 뒤, 동시에 위로 올라가며 공통 조상을 찾는 방식으로 진행됩니다.
def lca(u, v):
if depth[u] < depth[v]:
u, v = v, u # 항상 u가 더 깊게
# 1. 깊이를 같게 만들기
for i in range(LOG - 1, -1, -1):
if depth[u] - (1 << i) >= depth[v]:
u = parents[u][i]
# 2. 같은 노드면 그게 공통 조상
if u == v:
return u
# 3. 조상을 위로 같이 올려가며 찾기
for i in range(LOG - 1, -1, -1):
if parents[u][i] != -1 and parents[u][i] != parents[v][i]:
u = parents[u][i]
v = parents[v][i]
return parents[u][0]
최소 신장 트리 (Minimum Spanning Tree, MST)
모든 정점을 연결하면서 간선의 가중치 합이 최소가 되는 트리를 찾는 알고리즘입니다.
- 크루스칼 알고리즘 - 간선 중심으로 정렬 및 유니온 파인드 알고리즘을 사용하고 시간 복잡도는 O(E log E)입니다.
구현이 비교적 단순하지만 모든 간선을 정렬해야 해서 O(E log E)의 시간이 필요합니다.
def kruskal(n, edges):
parent = list(range(n))
def find(x):
while x != parent[x]:
parent[x] = parent[parent[x]]
x = parent[x]
return x
def union(x, y):
x_root = find(x)
y_root = find(y)
if x_root != y_root:
parent[y_root] = x_root
return True
return False
edges.sort(key=lambda x: x[2]) # 간선 가중치 기준 정렬
mst_weight = 0
for u, v, w in edges:
if union(u, v):
mst_weight += w
return mst_weight
- 프림 알고리즘 - 정점 중심 알고리즘으로 우선순위 큐를 사용하여 구현하고 시간 복잡도는 O(E log V)입니다.
정점 수가 적을 빼 빠르고 간선 정렬이 필요없으나 인접 리스트가 필요하고 그래프가 연결되어 있어야 한다는 단점이 있습니다.
import heapq
def prim(graph, start):
visited = [False] * len(graph)
hq = [(0, start)]
mst_weight = 0
while hq:
cost, u = heapq.heappop(hq)
if not visited[u]:
visited[u] = True
mst_weight += cost
for v, weight in graph[u]:
if not visited[v]:
heapq.heappush(hq, (weight, v))
return mst_weight
참고
https://namu.wiki/w/%EB%84%88%EB%B9%84%20%EC%9A%B0%EC%84%A0%20%ED%83%90%EC%83%89
https://velog.io/@gusdh2/DFS-vs-BFS-%EA%B9%8A%EC%9D%B4%EC%9A%B0%EC%84%A0%ED%83%90%EC%83%89-vs-%EB%84%88%EB%B9%84%EC%9A%B0%EC%84%A0%ED%83%90%EC%83%89
https://4legs-study.tistory.com/106
