힙 정렬
def heap_sort(iterable):
h = []
for value in iterable:
heapq.heappush(h, value)
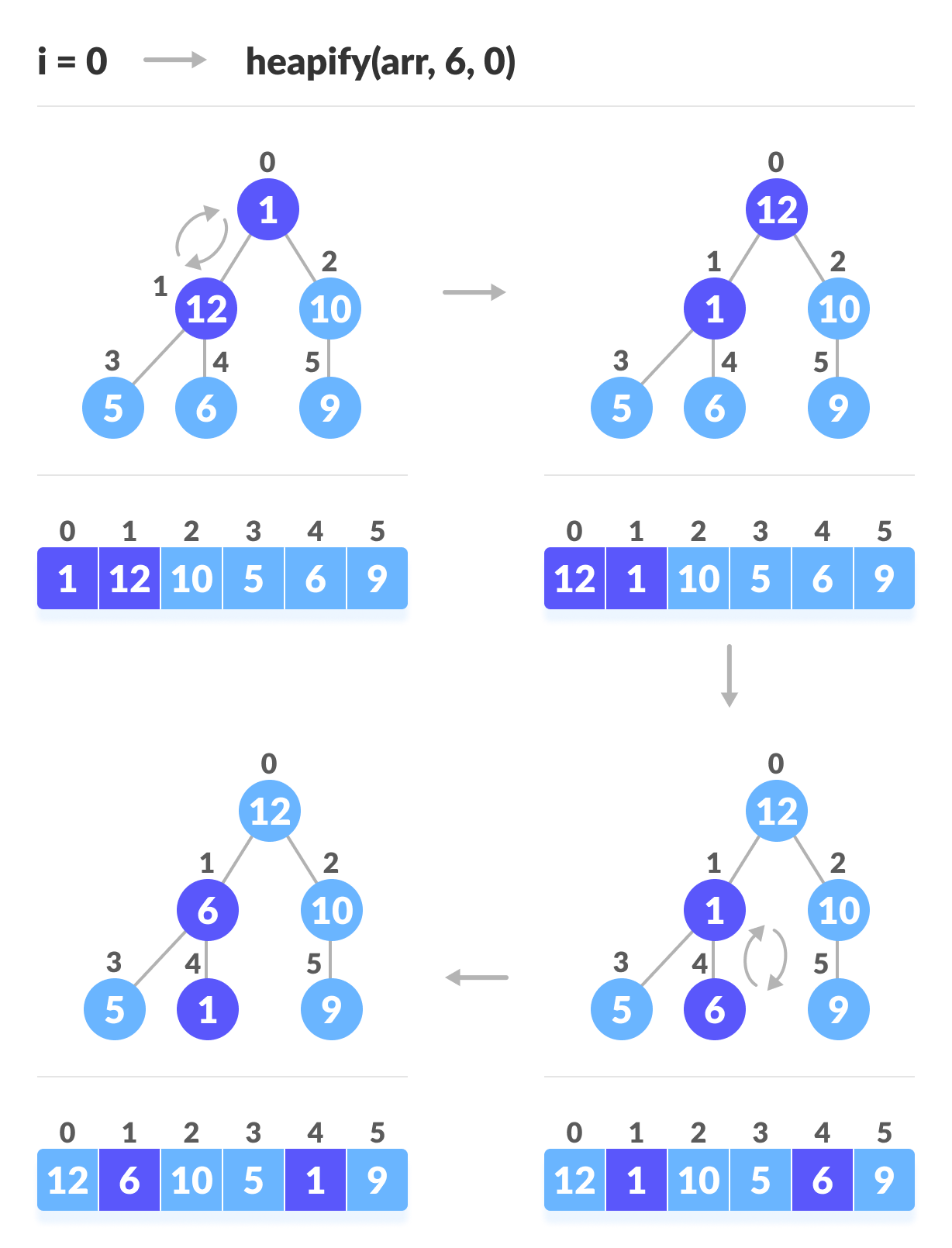
return [heapq.heappop(h) for _ in range(len(h))]힙 정렬은 완전 이진 트리 구조의 힙(heap)을 활용한 정렬 알고리즘입니다. 최대 힙을 구성한 후, 루트 노드(가장 큰 값)를 배열의 끝으로 보내고 다시 힙을 재구성하는 과정을 반복하며 정렬을 진행합니다.
정렬 대상 데이터 외에 추가적인 공간이 필요하지 않으므로 제자리 정렬이며, 최선, 평균 및 최악의 경우 모두 O(n log n) 의 시간 복잡도를 갖습니다.
다른 고급 정렬 알고리즘보다 구현이 약간 복잡할 수 있으나, 시간 복잡도가 안정적이고 재귀 없이 구현 가능하다는 장점이 있습니다. 하지만, 정렬된 결과를 얻기 위해 힙을 반복적으로 구성해야 하므로 실질적인 실행 시간에서는 퀵 정렬보다 느릴 수 있습니다.
기수 정렬
def radix_sort(arr):
exp = 1
max_val = max(arr)
while max_val // exp > 0:
buckets = [[] for _ in range(10)]
for num in arr:
buckets[(num // exp) % 10].append(num)
arr = [num for bucket in buckets for num in bucket]
exp *= 10
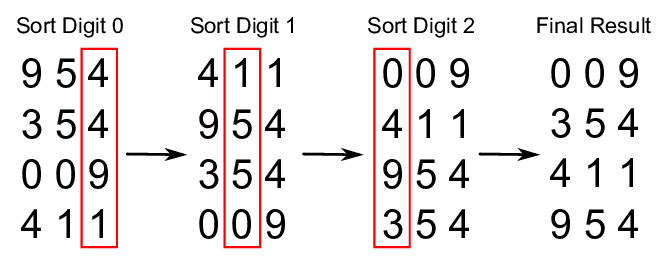
return arr기수 정렬은 각 자릿수를 기준으로 여러 번의 정렬을 수행해 전체 정렬을 완성하는 알고리즘입니다. 가장 낮은 자릿수부터 차례로 정렬하는 LSD(Least Significant Digit first) 방식이 일반적으로 사용됩니다. 각 자릿수 정렬에는 보통 안정 정렬인 계수 정렬(Counting Sort) 이 활용됩니다.
정렬 대상 데이터 외에 보조 배열이 필요하므로 제자리 정렬은 아니지만, 비교 연산 없이 정렬을 수행한다는 특징이 있습니다. 특히, 음수가 없고 자릿수가 작을수록 매우 빠른 성능을 보이는 정렬 알고리즘입니다.
최선, 평균, 최악의 경우 모두 O(nk) 의 시간 복잡도를 가지며 여기서 n은 데이터 수, k는 자릿수(최대값의 자릿수)를 의미합니다. 따라서 비교 기반 정렬처럼 O(n log n)보다도 더 빠르게 작동할 수 있는 경우도 존재합니다.
기수 정렬은 구현이 단순하고 숫자 기반 정렬에 매우 효과적이지만 음수나 실수, 문자열 같은 복잡한 데이터에는 직접적으로 사용하기 어렵고 추가 메모리 사용 측면에서 제한이 있을 수 있습니다. 또한 자릿수가 커질수록 반복 횟수가 많아지므로 항상 가장 빠른 정렬법은 아닙니다.
계수 정렬
def counting_sort(arr):
count = [0] * (max(arr) + 1)
for num in arr:
count[num] += 1
return [i for i, c in enumerate(count) for _ in range(c)]
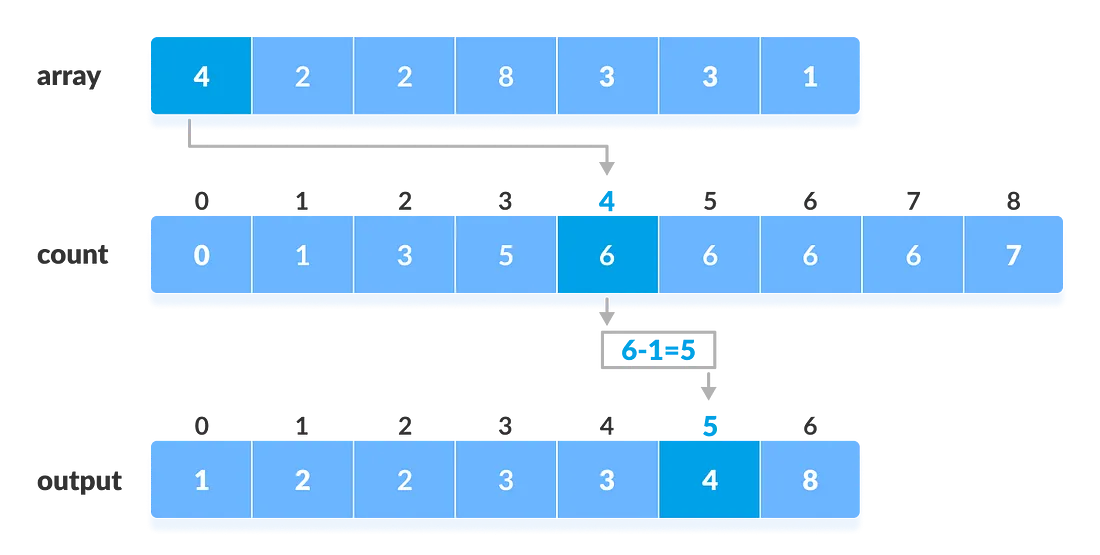
계수 정렬은 데이터의 크기를 기준으로 개수를 세어 정렬을 수행하는 알고리즘입니다. 비교 기반이 아닌 정렬 방식으로, 정수형 데이터이면서 범위가 제한적인 경우 매우 빠른 성능을 보입니다.
기본 아이디어는 각 값이 등장한 횟수를 카운팅 배열에 기록한 뒤 이를 누적하여 원래 배열에 순서대로 값을 채워 넣는 방식입니다. 원소 간 비교를 전혀 하지 않기 때문에 정렬 알고리즘 중에서도 가장 빠른 축에 속합니다.
다만, 계수 정렬은 데이터 값 자체를 인덱스로 활용하기 때문에 음수 데이터가 있을 경우 보정 처리가 필요하며 데이터가 희소하거나 최댓값이 너무 클 경우 메모리 낭비가 발생합니다.
시간 복잡도는 입력 크기를 n, 최댓값을 k라 했을 때 O(n + k) 이며 범위가 작을 경우 매우 효율적입니다. 추가 메모리 공간이 필요하므로 제자리 정렬은 아니지만 안정 정렬로 구현이 가능합니다.
계수 정렬은 범위가 좁은 정렬 문제에서 특히 유용하며, 내부적으로 기수 정렬의 보조 정렬로도 자주 사용됩니다.
이진 탐색
def binary_search(arr, target):
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid # 인덱스 반환
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
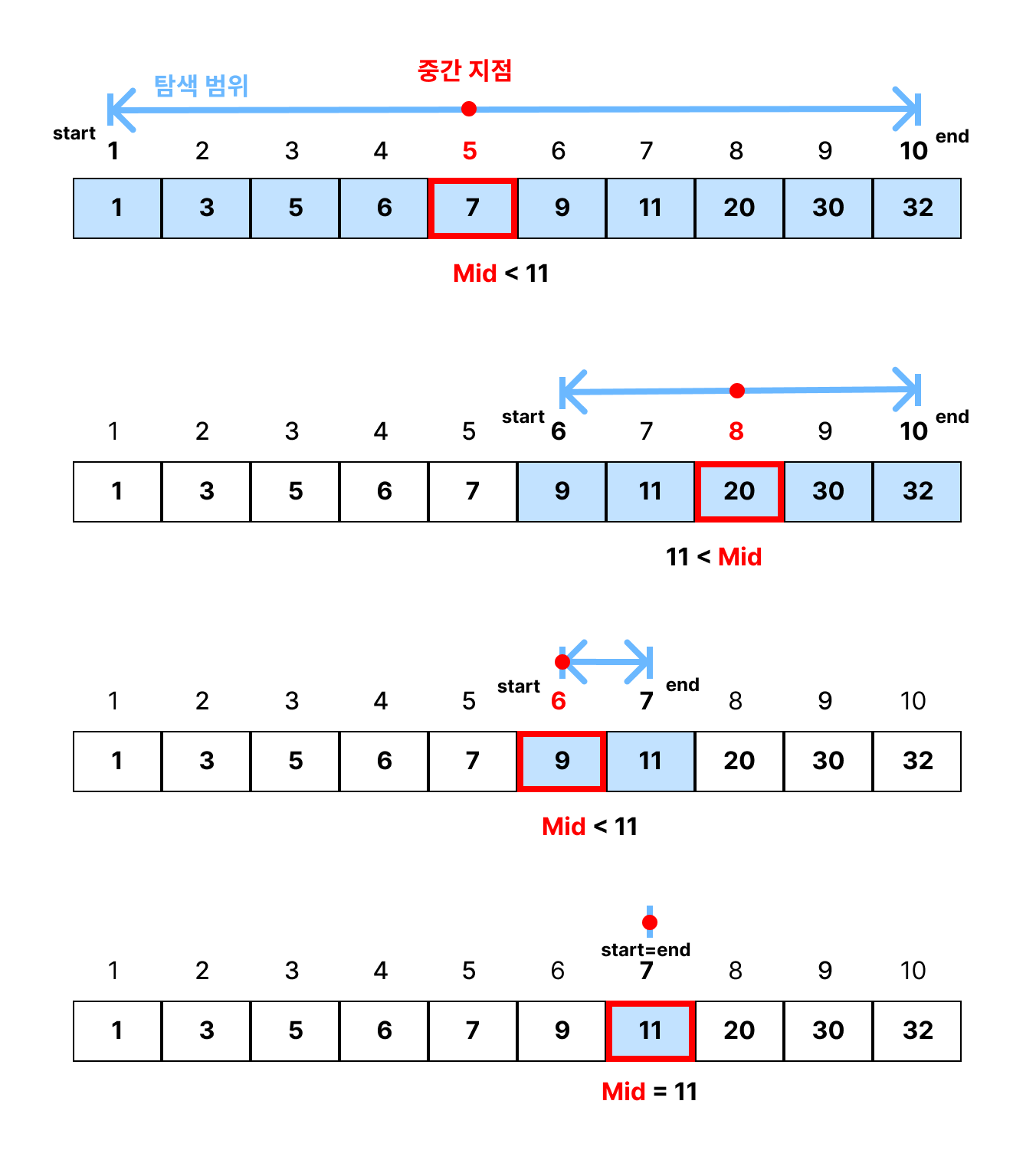
return -1 # 찾지 못한 경우이진 탐색은 정렬된 데이터를 빠르게 탐색하기 위해 사용되는 알고리즘입니다. 이 알고리즘은 정렬된 데이터를 전제로 작동하며 배열의 가운데 값을 기준으로 찾고자 하는 값과 비교하고 그 결과에 따라 탐색 범위를 절반으로 줄여가며 반복적으로 탐색을 진행합니다.
시간 복잡도는 평균과 최악의 경우 모두 O(log n)입니다. 데이터가 많아질수록 선형 탐색보다 훨씬 효율적으로 작동합니다. 최선의 경우에는 중간에 바로 값을 찾는 경우로 O(1)의 시간 복잡도를 가집니다.
이진 탐색은 삽입이나 삭제가 자주 일어나는 경우에는 정렬 상태를 유지해야 하므로 이진 탐색의 효율이 낮아질 수 있습니다. 그러나 데이터가 고정되어 있고 탐색이 주요 목적이라면 굉장히 효율적인 탐색 알고리즘이 될 수 있습니다.
참고
https://www.programiz.com/dsa/heap-sort
https://wikidocs.net/219635
https://velog.io/@shitaikoto/Algorithm-Radix-Sort
https://conanmoon.medium.com/%EB%8D%B0%EC%9D%B4%ED%84%B0%EA%B3%BC%ED%95%99-%EC%9C%A0%EB%A7%9D%EC%A3%BC%EC%9D%98-%EB%A7%A4%EC%9D%BC-%EA%B8%80%EC%93%B0%EA%B8%B0-%EC%8A%A4%EB%AC%BC-%EB%91%90%EB%B2%88%EC%A7%B8-%EC%9D%BC%EC%9A%94%EC%9D%BC-e65a8b7d872f
https://amaran-th.github.io/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98/[%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98]%20%EC%9D%B4%EC%A7%84%20%ED%83%90%EC%83%89/
