트리

트리는 계층 구조의 데이터를 표현하기 위한 자료구조

1. 트리는 Node들로 구성
2. Root (node)는 최상위 노드를 뜻함
3. Child (node)는 자식 노드
4. Parent (node)는 부모 노드 - root node를 제외한 각각의 node는 하나의 Parent node를 가짐
5. Leaf (node)는 Child node가 없는 node
6. 각각 노드는 level을 가짐 => level은 노드의 특정 깊이를 가리킴
7. Height (depth)는 tree의 총 레벨을 가리킴

Binary tree

각각의 노드를 최대 2개의 child node를 가진다.
-left child와 right child로 구분

노드의 child의 개수는 0, 1, 2 개중 하나로 구성

Full binary tree

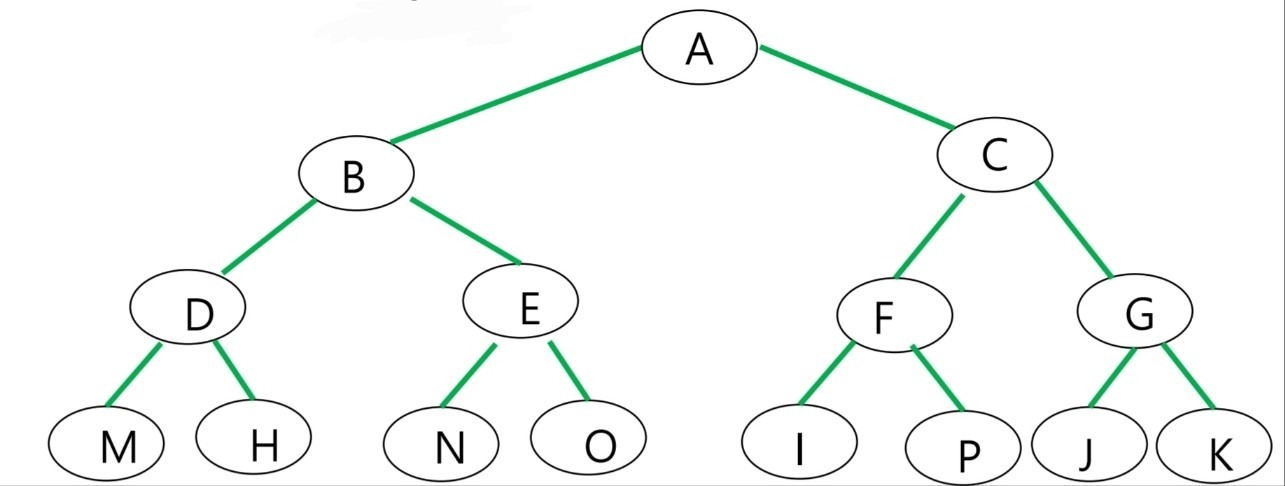
모든 노드가 2개의 child node로 구성 (단 leaf node)는 제외
height = h
Number of nodes = $2^h - 1$

Complete binary tree

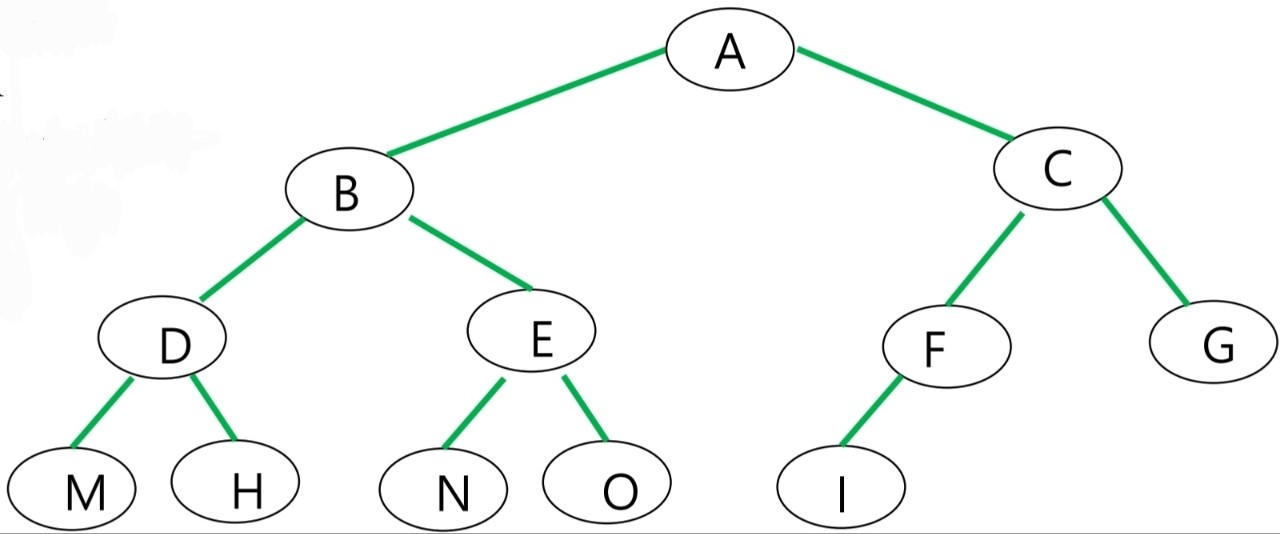
Full binary tree ⊂ Complete binary tree

height = h
Level: 0, 1, 2, 3, ..., h-1
Numver of nodes:
Min: $2^{h-1}$
Max: $2^h-1$ //full binary tree

Level 이 h-2까지 full binary tree이다.
Level h-1, 즉 leaf level에서는 rightmost leaf node 부터 순차적으로 삭제가 가능

Skewed binary tree

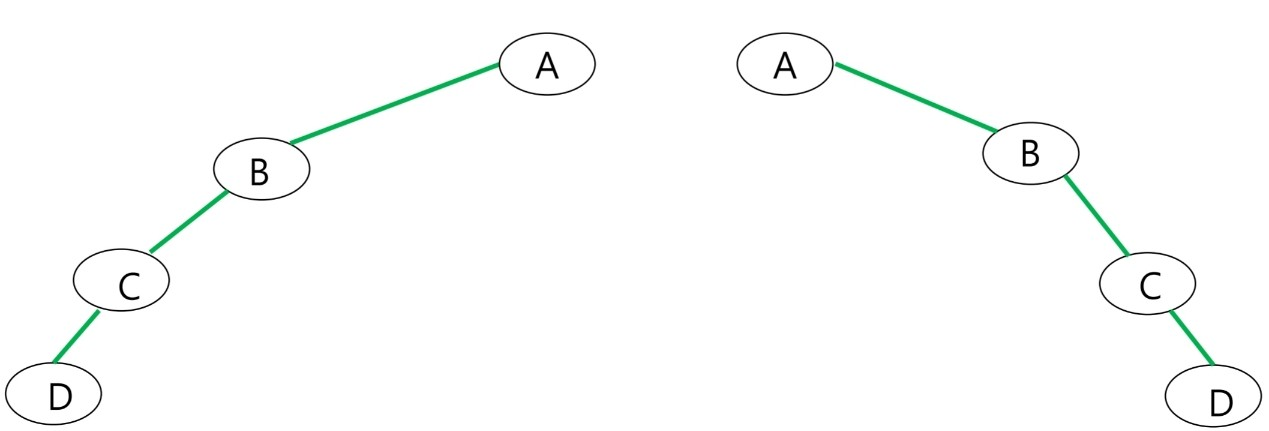
1. left skewed
2. right skewed

기울어진 height = numberof nodes의 트리로 구성

Binary tree 표현 방법

1. Array를 이용한 표현
   
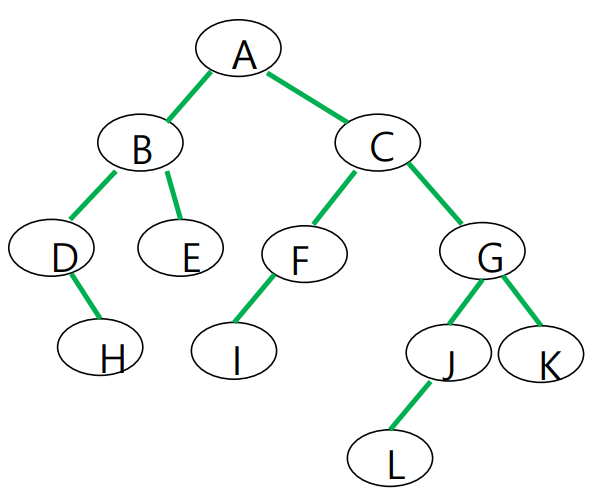
   tree의 형태가 다음과 같을 때, array로 다음과 같이 표현한다.
   
   array에서 root node는 index 1에 할당
   중간에 index가 8, 10, 11...이 비어있는 이유는 root node부터 leaf노드까지 배열에 할당되어 있는데 중간 중간 노드가 비어있기 때문이다.

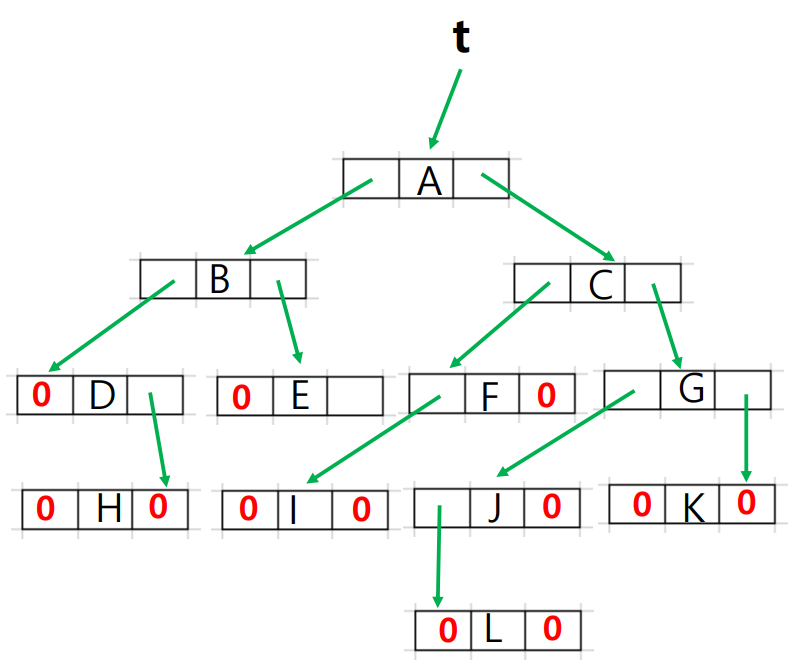
2. linked를 이용한 표현
   node의 형태를 다음과 같이 표현한다.
   
   data에 값을 넣고 left child와 right child를 가리키는 링크를 생성한다.
   
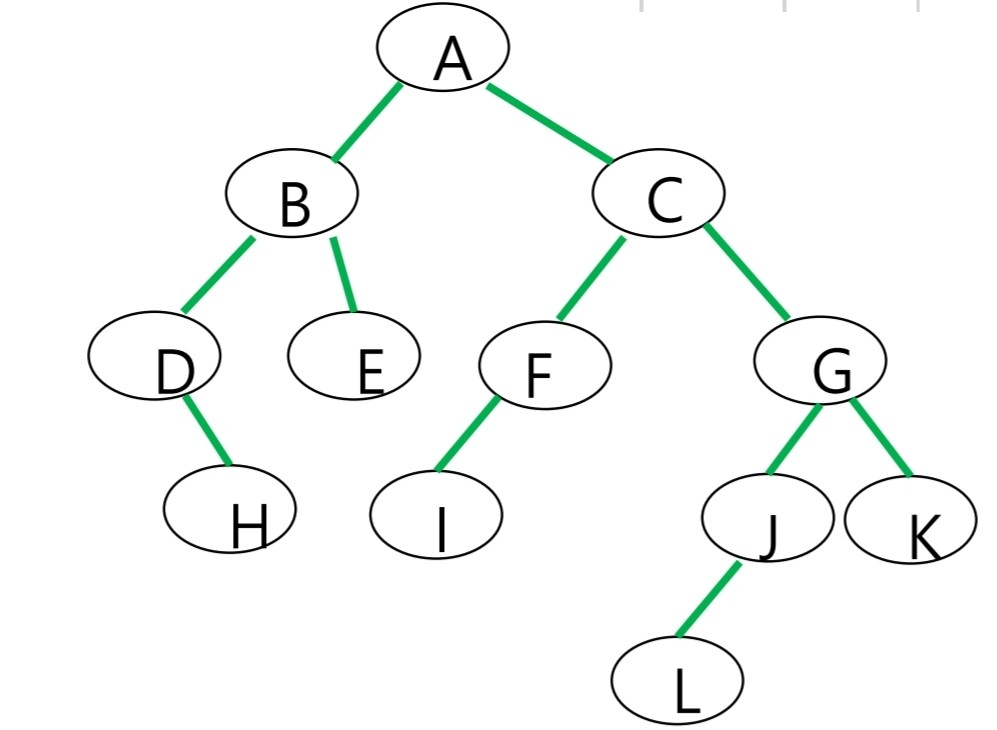
   tree가 다음과 같이 구성되어 있을 때 linked를 이용해서 다음과 같이 표현을 한다.
   

Binary tree의 탐색 방법

• Preorder: root -> Left subtree -> Right subtree 순으로 탐색
• Inorder: Left subtree -> root -> Right subtree 순으로 탐색
• Postorder: Left subtree -> Right subtree -> root 순으로 탐색
  

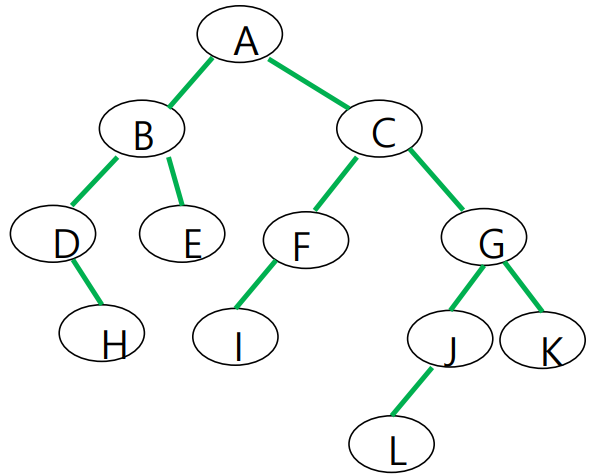
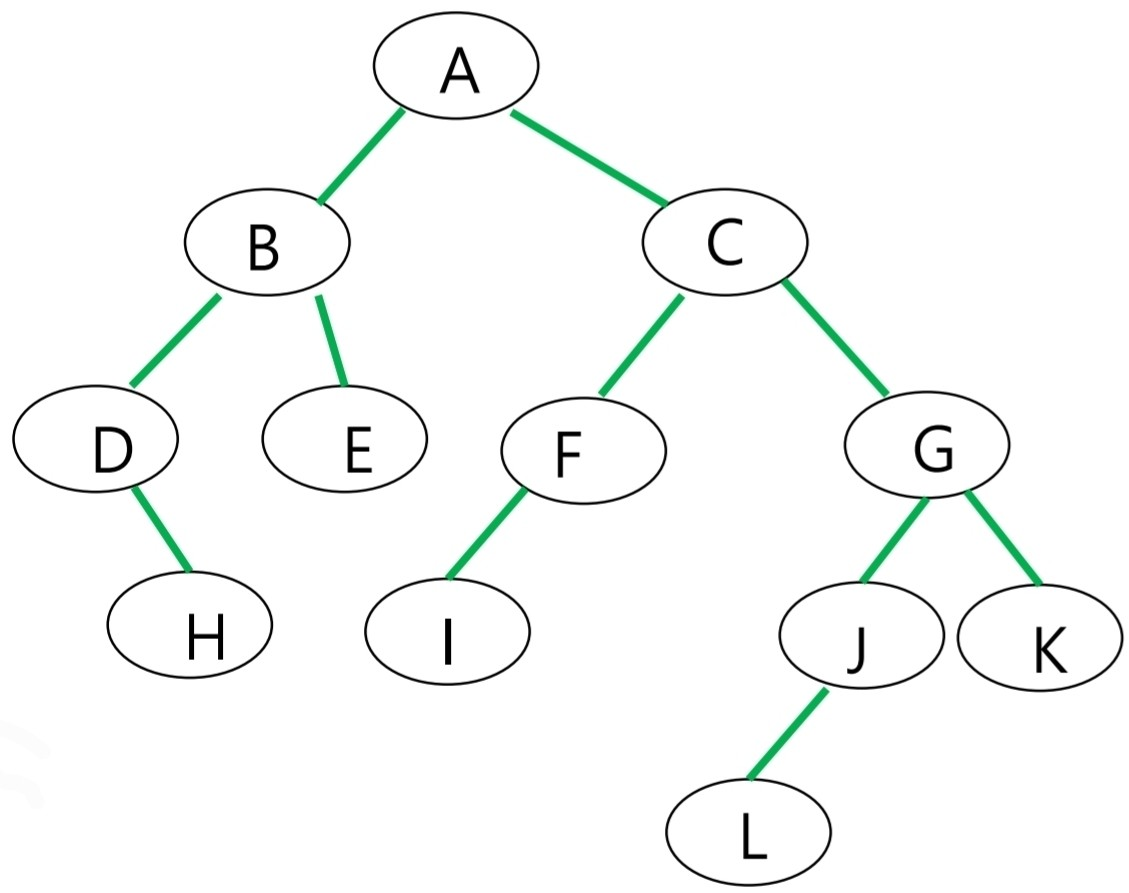
트리가 다음과 같이 구성되어 있을 때

• Preorder: A -> B -> D -> H -> E -> C -> F -> I -> G -> J -> L -> K
• Inorder: D -> H -> B -> E -> A -> I -> F -> C -> L -> J -> G -> K
• Postorder: H -> D -> E -> B -> I -> F -> L -> J -> K -> G -> C -> A

Heap

1. Max(Min) tree

   • Binary tree
   • child node 보다 작(크)지 않음

2. Max(Min) heap

   • Complete binary tree
   • Max(Min) tree -> 대소관계 구성

3. Max(min) priority queue

   • 요소가 우선순위가 있음

Heap의 표현 방법

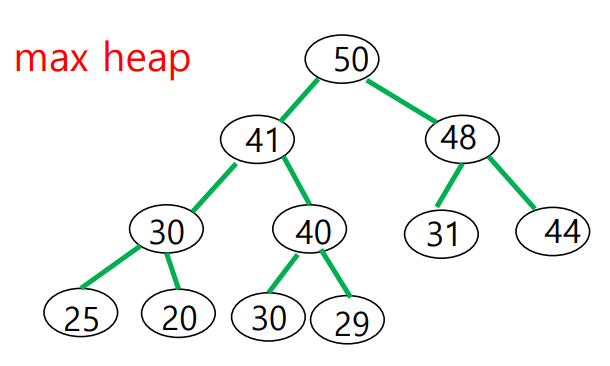
• Array를 이용해 표현
  

heap의 insert와 delete의 시간복잡도

O(h) = O(log n)

Heap - insert

A[i]의 parent node : A[ ⌊1/2⌋ ]

Heap - delete

Heap sort

step

1. root node와 rightmost leaf node 를 바꾼다.
2. heap tree를 재조정한다.
3. 1&2를 sorting이 될 때까지 반복한다.