밀린 React, Express, Pandas를 뒤로하고..
17주차 복습 시작!

🤷‍♀️ 딥러닝?

인공지능(Artificial Inteligence)

머신러닝(Machine Learning)

딥러닝(Deep Learning)

딥러닝은 인공신경망에 기반하여 컴퓨터에게 사람의 사고방식을 가르치는 방법으로 보통 모델의 입력층(Input Layer) 과 출력층(Output Layer) 사이에 존재하는 히든 레이어(Hidden Layer) 가 3층 이상일 때 딥러닝 이라고 한다.

• 인공신경망 : 사람의 신경 시스템을 모방
  - 특징 : 모델 스스로 데이터의 특성을 학습 => 지도/비지도 학습 모두 가능

🧐 퍼셉트론(Perceptron)

• 사람의 뉴런 과 같은 역할을 하는 모델로 초기 형태의 신경망

• 등장 배경: 명시적 프로그래밍의 한계(모든 조건을 고려할 수 없음)
  => 모델 스스로 데이터를 판단할 수 있는 기술이 필요

• 구조: 입력값과 각각의 가중치를 곱하여 더한 후 bias를 더한 값을 활성함수(activation)에 넣음
  

• activation function의 경우 step function으로 일정 값을 넘으면 1, 그렇지 않으면 0 형태의 값을 가짐

✍ 단층 퍼셉트론(Single Layer Perceptron)

• 입력층과 출력층으로만 이루어진 단층 퍼셉트론으로 논리회로 구현 및 선형 분류 가능
  ex> AND Gate, OR Gate, NAND Gate, NOR Gate , ...

✍ 다층 퍼셉트론(Multi Layer Perceptron)

• XOR Gate 와 같이 선형 분류로 해결할 수 없는 비선형적 문제 발생
  ex> XOR

x1	x2	output
0	0	0
0	1	1
1	0	1
1	1	0

=> 단층 퍼셉트론을 여러층으로 쌓아 비선형적 문제 해결
=> XOR의 경우 NAND 와 OR 을 결합하여 구현 가능

• 입력층, 출력층 외에 쌓여져 있는 여러 층을 Hidden Layer라고 함
• 이 Hidden Layer 가 3층 이상이면 딥러닝

🧐 딥러닝 모델

✍ 구성 요소

• Node/Unit : 각 층을 구성하는 요소
• Weight : 각 노드를 연결하는 강도(=가중치)
• Layer : 모델을 구성하는 층

✍ 학습 방법

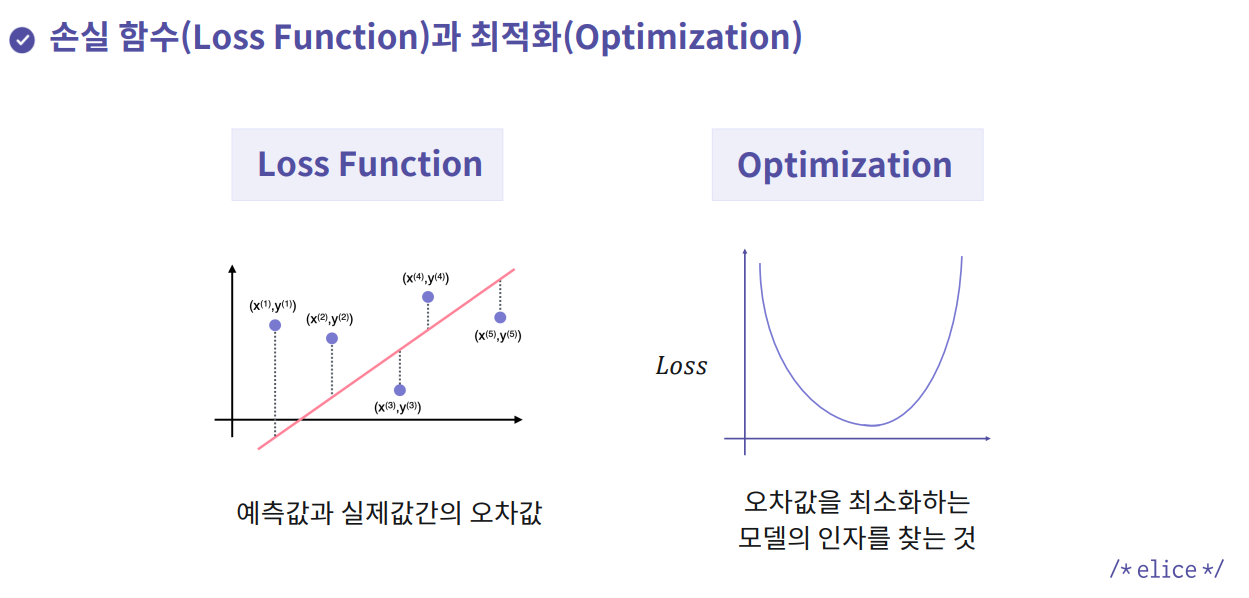
• Loss Function 을 최소화하기 위해 최적화 알고리즘 Optimizer을 적용

• 예측값과 실제값간의 오차값을 줄이기 위해 오차값을 최소화하는 인자를 찾는 알고리즘을 적용
  

• loss function : 예측값과 실제값 간 오차값
  ex> MAE, MSE, RMSE, Cross entropy

• 기본적인 최적화 알고리즘 : GD(Gradient Descent)
  - 손실함수의 값을 최소화하기 위해 특정 가중치의 기울기(Gradient)를 이용하는 방법
  - W(t+1) = W(t) - lr * dLoss(W)

  • W(t) : t번째 가중치
  • lr: 학습률(Learning Rate)
  • dLoss(W): 해당 가중치에서 손실함수의 기울기(미분)

• 각 가중치의 기울기 구하는 방법 : 역전파(Back Propagation)
  - 역전파(Back Propagation) : 목표 값과 모델이 예측한 output 값의 오차를 구하여 다시 뒤로 전파하면서 변수 값을 갱신하는 알고리즘
  - 순전파(Forward Propagation) : 입력값을 바탕으로 출력값을 계산하는 과정

🧐 딥러닝의 문제점

1. 학습 속도 문제
2. 기울기 소실 문제
3. 초기값 설정 문제
4. 과적합 문제

✍ 학습 속도 문제

• 원인
  데이터 개수가 많아지면서 전체 데이터를 사용하여 손실함수를 계산할 때 계산량이 증가 => 속도가 낮아짐

• 해결 방법
  전체 데이터가 아닌 부분 데이터를 활용하여 손실 함수를 계산
  => SGD(Stochastic Gradient Descent)

• SGD(Stochastic Gradient Descent)
  - 전체 데이터(batch)가 아닌 일부 데이터(mini-batch)에 대해 손실함수 계산
  - 정확도는 떨어지지만 계산 속도가 빠름 => 많은 step 진행 가능
  - 한계
  1) mini-batch에 따른 Gradient 방향에 대한 문제 발생
  2) Learning Rate가 너무 크거나 작은 경우 최적값 찾기가 어려움

• 다양한 최적화 알고리즘 등장
  - SGD의 Gradient 방향 해결 : Momentum -> Adam
  - SGD의 Learning Rate 관련 문제 해결: AdaGrad -> RMSProp -> Adam

• Adam : Momentum의 장점과 RMSProp의 장점을 결합한 최적화 알고리즘

✍ 기울기 소실 문제

• 원인
  더 깊고 넓은 망을 학습시키면서 역전파시 출력값과 멀어질 경우 학습이 잘 안되는 문제 발생 -> sigmoid 사용시 역전파할때 기울기가 0인 값을 전달하며 중간값 소실 -> 기울기 소실 문제가 반복되며 학습 제대로 안됨
• 해결 방법
  activation function 으로 sigmoid 대신
  ReLU(내부 히든층) / tanh (외부 출력층) 사용

✍ 초기값 설정 문제

• 원인
  초기값을 잘못 설정할 경우 성능 차이가 크게 발생

• 해결 방법
  활성화 함수의 입력값이 너무 커지거나 작아지게 하면 안됨
  - 1. 표준 정규분포 / 표준편차를 0.01로 하는 정규 분포로 초기화
  - 2. Xavier 초기화 방법 + Sigmoid
Xavier : 표준 정규분포를 입력개수의 제곱근으로 나누어줌

  🚩 ReLU 함수에는 Xavier초기화가 적합하지 않음
  레이어를 거칠수록 값이 0에 수렴

  - 3. He 초기화 방법 + ReLU
He : 표준 정규분포를 입력개수의 절반의 제곱근으로 나누어줌

Sigmoid, tanh 에는 Xavier, ReLU 에는 He가 효율적

✍ 과적합 문제

• 원인
  train data에 과적합하여 실제 데이터에 대한 예측 성능 저하
• 해결 방법
• 1. 정규화(Regularization) : 기존 손실함수에 규제항을 더해 최적값 찾기 가능
  • 1) L1 정규화 (Lasso Regularization)
    가중치의 절댓값의 합을 규제항으로 정의
    작은 가중치가 거의 0으로 수렴함 -> 몇 개의 중요한 가중치만 남음
  • 2) L2 정규화 (Ridge Regularization)
    가중치의 제곱의 합을 규제항으로 정의
    큰 값을 가진 가중치를 제약하는 효과
• 2. 드롭아웃(Dropout) : 각 layer마다 일정 비율의 뉴런(node)을 임의로 drop
     -> 학습되는 노드와 가중치들이 매번 달라짐
  • 다른 정규화 기법과 상호 보완적으로 사용 가능
    -> backpropagation 할때 신호를 끊음
• 3. 배치 정규화(Batch Normalization)
     : normalization을 input data 뿐만 아니라 hidden layer의 input에도 적용
  • layer마다 정규화를 진행해서 초기화 중요도 감소
  • 과적합 억제(Dropout, L1, L2 정규화 필요성 감소)
  • 핵심은 학습 속도의 향상

출처: /*elice*/ 수업 자료